Difference–Differential Equations

Abstract

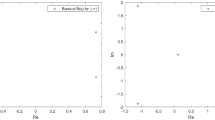
THE general linear homogeneous difference–differential equation with constant coefficients is where 0 ⩽ μ ⩽m, 0⩽ν ⩽ n, y^(ν)(t) is the ν-th derivative of the unknown function y (t) and 0 = b₀ < b₁ < ... < b_m. Particular examples of this equation have appeared in radiology^1,2, economics^3,4 and the theory of control mechanisms^5,6. The most useful ‘boundary conditions’ are also the most convenient from the theoretical point of view ; We suppose assigned the values of y (t) in an initial interval 0 ⩽< t < b_m. In terms of these given values, we define a function (In particular cases this usually reduces to something fairly simple.) It is obvious that y = exp st is a solution of (1) for any s satisfying . The zeros of τ(S) are infinite in number ; but their asymptotic behaviour is readily calculable⁷. Under suitable conditions, the solution of (1) is where s runs through all the zeros of τ(s). I here assume that τ(s) has no double zero ; if it has, a slight modification must be made in the corresponding term. The series in (2) is convergent and its sum is y (t) (i) for all t, if a_mn≠ 0 and a_0n ≠ 0, and (ii) for all t > b_m, if a_mn≠ 0. (2) Was first given by Hilb⁸, but under conditions which would exclude most of the applications. A detailed proof of its validity under the conditions stated will be published shortly⁹.