Abstract
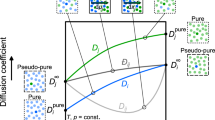
THE diffusion coefficient of a particle in solution is given by the Einstein equation1: 
where f is the frictional coefficient of the diffusing substance.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Similar content being viewed by others
References
Einstein, A., Ann. der Phys., 17, 549 (1905).
Stokes, G. G., Camb. Trans., 9, 8, Papers III, 1 (1851).
Basset, quoted by Lamb in Hydrodynamics, 602 (New York, 1945).
Sutherland, W., Phil. Mag., 9, 6 (1905).
Rossi, C., Bianchi, E., and Rossi, A., J. Chim. Phys., 55, 97 (1958).
Rossi, C., Bianchi, E., and Rossi, A., J. Chim. Phys., 55, 91 (1958). Rossi, C., and Bianchi, E., La Chimica e l'Industria, 40, 992 (1958).
Rossi, C., and Bianchi, E., J. Polymer Sci., 41, 189 (1959).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
ROSSI, C., BIANCHI, E. Diffusion of Small Molecules. Nature 189, 822–824 (1961). https://doi.org/10.1038/189822a0
Issue date:
DOI: https://doi.org/10.1038/189822a0
This article is cited by
-
Chemically-powered swimming and diffusion in the microscopic world
Nature Reviews Chemistry (2021)
