Discriminant Analysis in Biometrical Genetics

Abstract

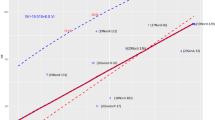
SEVERAL notable attempts have been made to analyse and interpret the inheritance of polygenic characters in terms of simple Mendelian factors giving the familiar ratios in segregating generations^1,2. More recently, Weber^3,4 proposed his so-named discriminant analysis technique, in which two or more component measurements of a character that may individually appear to be normally distributed are combined into a discriminant function which, in contrast, might assume generally a bimodal frequency distribution suggesting this linear compound measure to be simply inherited like qualitative traits. He illustrates this method for the cotyledon size in tomato by using a linear function of length/width ratio (x₁) and area (x₂), x = b₁x₁ + b₂x₂, and showing x to have a bimodal frequency distribution in F₂ that simulated a segregation ratio of 3 : 1 in one case and of 9 : 7 in the other. Apparently, Dr. Weber considers this method of analysing quantitative characters to be useful in general as he argues³, “this total measurement of discriminant function has no dimensional designation; it is without dimension in the physical sense, like the term red or white colour”.