An Iterative Method for obtaining Statistical Frequency Distributions

Abstract

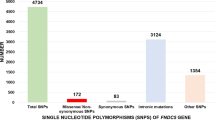
SINCE when two samples from a population are combined we get a larger and more representative sample, the iterative process could, in effect, be considered as a means of obtaining a larger sample starting from a small one. As the distribution curve F₂ is derived from the mean values of the frequencies in F and F₁, that is, (F + F₁)/2, the result of the combination of two sets of data, namely, the actual curve obtained from n experiments and its Gaussian counterpart, may be regarded as being representative of 2n experimental observations (Fig. 1). On the same basis, we may regard F₃ (derived from F₂ and F₁) as representing 3n experimental observations and F₄, 5n experimental observations. Thus the sample size may be considered as increasing in the following sequence, namely, n, n, 2n, 3n, 5n, … 89n, … corresponding to F, F₁, F₂, F₃, F₄, …, F₁₀ and so forth. The (n + 1)^th term in this sequence is given by We have since found that a more rational procedure would be to use instead of to get F₂, instead of to get F₃, and so forth. The results obtained by this modification are, however, not significantly different from those obtained previously. But the latter procedure may be considered more logical as indicative of the increase in equivalent sample size.