Measurement of Surface Tension by Interferometric Means

Abstract

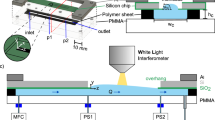
FOR a sessilo drop of liquid of surface tension, density and radius of curvature R₀ at the vertex, the differential equation¹: for drop shape (Fig, 1) in terms of the co-ordinates measured from the vertex and scaled with respect to R₀, has recently been solved numerically on a digital computer by Staicopolus² and the Fortran II programme is available. The method used is more accurate than the elaborate approximation procedure of Bashforth and Adams¹ and, although not mentioned by Staicopolus, the results are also more accurate than Porter's³ values of γ/ρgr as a function of h/r. The results allow γ and r/R₀ to be related to h and r through a polynomial expression in z = (r/h − A)/C.