Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Properties of discrete electrostatic systems

Nature volume 320, pages 597–600 (1986)Cite this article

Abstract

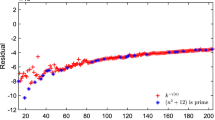
Further to a recent controversy1–5, it is well known that continuous classical electrostatics6,7 is an approximate description which smoothes the ‘microscopic irregularities’7 of discrete systems. Our purpose here is to highlight these microscopic details. We have studied the stability, Coulomb potential energy (W), electrostatic potential (V) and field intensity (E) for several arrangements of N point charges q on and inside the surface of a sphere of radius R (N≤20). As expected, discrete and continuous configurations differ in several respects. The energy form-factor w = W/N2 for a surface-charged sphere ranges from 0.l25q2/R at N = 2 to 0.377 q2/R at N = 20 (the latter value is ∼75% of the continuous limit, 0.5 q2/R). The field intensity inside the sphere is non-zero in the discrete case, but quickly tends, with increasing N, towards the continuous limit (zero). The common practice of treating small-N physical systems as continuous conceals properties that would otherwise be obvious.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Similar content being viewed by others

References

  1. Berezin, A. A. Nature 315, 104 (1985).

    Article  ADS  Google Scholar 

  2. MacGowan, D. Nature 315, 635 (1985).

    Article  ADS  Google Scholar 

  3. Nityananda, R., Cormack, A. M., Naumann, R. A. & Webb, S. Nature 316, 301–302 (1985).

    Article  ADS  Google Scholar 

  4. Queen, N. M., Rees, M. & Berezin, A. A. Nature 317, 208 (1985).

    Article  ADS  Google Scholar 

  5. Aspden, H. Nature 319, 8 (1986).

    Article  ADS  Google Scholar 

  6. Jeans, J.H. The Mathematical Theory of Electricity and Magnetism 5th edn, 36, 42 (Cambridge University Press, 1933).

    Google Scholar 

  7. Morse, P. M. & Feshbach, H. Methods of Theoretical Physics Vol. 1, 201 (McGraw-Hill, New York, 1953).

    MATH  Google Scholar 

  8. Leech, J. Mathl Gaz. 41, 81–90 (1957).

    Article  Google Scholar 

  9. Fejes Toth, L. Regular Figures, 102–123, 157 (Pergamon, Oxford, 1964).

    Book  Google Scholar 

  10. Coxeter, H. S. M. Regular Polytopes, 33–57 (Methuen, London, 1948).

  11. King, R. B. J. Am. chem. Soc. 92, 6455–6466 (1970).

    Article  CAS  Google Scholar 

  12. Melnyk, T. W., Knop, O. & Smith, W. R. Can. J. Chem. 55, 1745–1761 (1977).

    Article  CAS  Google Scholar 

  13. Fejes Toth, L. Am. J. Math. 70, 174–180 (1948).

    Article  Google Scholar 

  14. Whyte, L. L. Am. math. Mont. 59, 606–611 (1952).

    Article  Google Scholar 

  15. Foppl, L. J. reine angew. Math. 141, 251–302 (1912).

    MathSciNet  Google Scholar 

  16. Goldberg, M. Maths Comput. 23, 785–786 (1969).

    Article  Google Scholar 

  17. Cohn, H. Mathl Tabl. natn. Res. Counc., Wash. 10, 117–120 (1956).

    Google Scholar 

  18. Lin, Y. C. & Williams, D. E. Can. J. Chem. 51, 312–316 (1973).

    Article  CAS  Google Scholar 

  19. Claxton, T. A. & Benson, G. C. Can. J. Chem. 44, 157–163; 1730–1731 (1966).

    Article  CAS  Google Scholar 

  20. Britton, D. Can. J. Chem. 41, 1632–1634 (1963).

    Article  CAS  Google Scholar 

  21. Evans, R. D. The Atomic Nucleus, 32–39 (McGraw-Hill, New York, 1955).

  22. Singh, D., Varshni, Y. P. & Dutt, R. Phys. Rev. A32, 619–622 (1985).

    Article  ADS  CAS  Google Scholar 

  23. Patil, S. H. Phys. Rev. A24, 2913–2919 (1981).

    Article  ADS  MathSciNet  CAS  Google Scholar 

  24. Mehta, C. H. & Patil, S. H. Phys. Rev. A17, 43–46 (1978).

    Article  ADS  Google Scholar 

  25. Hefter, E. F. Phys. Rev. A32, 1205–1027 (1985).

    Article  ADS  CAS  Google Scholar 

  26. Elton, L. R. B. Nuclear Sizes (Oxford University Press, 1961).

    Google Scholar 

  27. Maddox, J. Nature 313, 93 (1985).

    Article  ADS  Google Scholar 

  28. Mortley, W. S. Nature 313, 638 (1985).

    Article  Google Scholar 

  29. Schrack, R. A. Nature 314, 324 (1985).

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Swiss Federal Institute of Technology, Institute of Energy Technology, Nuclear Engineering Laboratory, ETH-Zentrum, CH-8092, Zurich, Switzerland

    Hector A. Munera

Authors
  1. Hector A. Munera
    View author publications

    Search author on:PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Munera, H. Properties of discrete electrostatic systems. Nature 320, 597–600 (1986). https://doi.org/10.1038/320597a0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/320597a0

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing