Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Scaling macroscopic aquatic locomotion

Nature Physics volume 10, pages 758–761 (2014)Cite this article

Subjects

Abstract

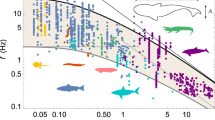
Inertial aquatic swimmers that use undulatory gaits range in length L from a few millimetres to 30 metres, across a wide array of biological taxa. Using elementary hydrodynamic arguments, we uncover a unifying mechanistic principle characterizing their locomotion by deriving a scaling relation that links swimming speed U to body kinematics (tail beat amplitude A and frequency ω) and fluid properties (kinematic viscosity ν). This principle can be simply couched as the power law Re ∼ Swα, where Re = UL/ν ≫ 1 and Sw = ω AL/ν, with α = 4/3 for laminar flows, and α = 1 for turbulent flows. Existing data from over 1,000 measurements on fish, amphibians, larvae, reptiles, mammals and birds, as well as direct numerical simulations are consistent with our scaling. We interpret our results as the consequence of the convergence of aquatic gaits to the performance limits imposed by hydrodynamics.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Aquatic swimming.
Figure 2: Scaling aquatic locomotion: measurements.
Figure 3: Scaling aquatic locomotion: simulations.

Similar content being viewed by others

References

  1. Pedley, T. J. Scale Effects in Animal Locomotion (Cambridge Univ. Press, 1977).

    Google Scholar 

  2. Vogel, S. Life in Moving Fluids: The Physical Biology of Flow (Princeton Univ. Press, 1996).

    Google Scholar 

  3. Fish, F. E. & Lauder, G. V. Passive and active flow control by swimming fishes and mammals. Annu. Rev. Fluid Mech. 38, 193–224 (2006).

    Article  ADS  MathSciNet  Google Scholar 

  4. Childress, S. Mechanics of Swimming and Flying (Cambridge Univ. Press, 1981).

    Book  Google Scholar 

  5. Hertel, H. Structure, Form, Movement (Reinhold, 1966).

    Google Scholar 

  6. Triantafyllou, M. S., Triantafyllou, G. S. & Yue, D. K. P. Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 32, 33–53 (2000).

    Article  ADS  MathSciNet  Google Scholar 

  7. Wu, T. Y. Fish swimming and bird/insect flight. Annu. Rev. Fluid Mech. 43, 25–58 (2011).

    Article  ADS  MathSciNet  Google Scholar 

  8. Bainbridge, R. The speed of swimming of fish as related to size and to the frequency and amplitude of the tail beat. J. Exp. Biol. 35, 109–133 (1958).

    Google Scholar 

  9. Webb, P. W., Kostecki, P. T. & Stevens, E. D. The effect of size and swimming speed on locomotor kinematics of rainbow trout. J. Exp. Biol. 109, 77–95 (1984).

    Google Scholar 

  10. Videler, J. J. & Wardle, C. S. Fish swimming stride by stride: speed limits and endurance. Rev. Fish Biol. Fisheries 1, 23–40 (1991).

    Article  Google Scholar 

  11. Mchenry, M., Pell, C. & Long, J. H. Jr Mechanical control of swimming speed: Stiffness and axial wave form in undulating fish models. J. Exp. Biol. 198, 2293–305 (1995).

    Google Scholar 

  12. Long, J. H. Jr Muscles, elastic energy, and the dynamics of body stiffness in swimming eels. Am. Zool. 38, 771–792 (1998).

    Article  Google Scholar 

  13. Taylor, G. I. Analysis of the swimming of long and narrow animals. Proc. R. Soc. Lond. A 214, 158–183 (1952).

    Article  ADS  Google Scholar 

  14. Lighthill, M. J. Large-amplitude elongated-body theory of fish locomotion. Proc. R. Soc. Lond. B 179, 125–138 (1971).

    Article  ADS  Google Scholar 

  15. Hess, F. & Videler, J. J. Fast continuous swimming of saithe (Pollachius virens): A dynamic analysis of bending moments and muscle power. J. Exp. Biol. 109, 229–251 (1984).

    Google Scholar 

  16. Cheng, J. Y., Pedley, T. J. & Altringham, J. D. A continuous dynamic beam model for swimming fish. Phil. Trans. R. Soc. Lond. B 353, 981–997 (1998).

    Article  Google Scholar 

  17. McMillen, T., Williams, T. & Holmes, P. Nonlinear muscles, passive viscoelasticity and body taper conspire to create neuromechanical phase lags in anguilliform swimmers. PLoS Comput. Biol. 4, e1000157 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  18. Alben, S., Witt, C., Baker, T. V., Anderson, E. & Lauder, G. V. Dynamics of freely swimming flexible foils. Phys. Fluids 24, 051901 (2012).

    Article  ADS  Google Scholar 

  19. Kern, S. & Koumoutsakos, P. Simulations of optimized anguilliform swimming. J. Exp. Biol. 209, 4841–4857 (2006).

    Article  Google Scholar 

  20. Gazzola, M., van Rees, W. M. & Koumoutsakos, P. C-start: Optimal start of larval fish. J. Fluid Mech. 698, 5–18 (2012).

    Article  ADS  MathSciNet  Google Scholar 

  21. Tytell, E. D., Hsu, C. Y., Williams, T. L., Cohen, A. H. & Fauci, L. J. Interactions between internal forces, body stiffness, and fluid environment in a neuromechanical model of lamprey swimming. Proc. Natl Acad. Sci. USA 107, 19832–19837 (2010).

    Article  ADS  Google Scholar 

  22. Tytell, E. D. et al. Disentangling the functional roles of morphology and motion in the swimming of fish. Integr. Comp. Biol. 50, 1140–1154 (2010).

    Article  Google Scholar 

  23. Bhalla, A. P. S., Griffith, B. E. & Patankar, N. A. A forced damped oscillation framework for undulatory swimming provides new insights into how propulsion arises in active and passive swimming. PLoS Comput. Biol. 9, e1003097 (2013).

    Article  ADS  MathSciNet  Google Scholar 

  24. van Rees, W. M., Gazzola, M. & Koumoutsakos, P. Optimal shapes for anguilliform swimmers at intermediate Reynolds numbers. J. Fluid Mech. 722, R3 (2013).

    Article  ADS  Google Scholar 

  25. Batchelor, G. K. An Introduction to Fluid Dynamics (Cambridge Univ. Press, 1967).

    MATH  Google Scholar 

  26. Landau, L. D. & Lifshitz, E. M. Fluid Mechanics (Pergamon Press, 1959).

    Google Scholar 

  27. Horner, A. M. & Jayne, B. C. The effects of viscosity on the axial motor pattern and kinematics of the African lungfish (Protopterus annectens) during lateral undulatory swimming. J. Exp. Biol. 211, 1612–1622 (2008).

    Article  Google Scholar 

  28. Gazzola, M., Chatelain, P., van Rees, W. M. & Koumoutsakos, P. Simulations of single and multiple swimmers with non-divergence free deforming geometries. J. Comput. Phys. 230, 7093–7114 (2011).

    Article  ADS  MathSciNet  Google Scholar 

  29. Gazzola, M., Hejazialhosseini, B. & Koumoutsakos, P. Reinforcement learning and wavelet adapted vortex methods for simulations of self-propelled swimmers. SIAM J. Sci. Comput. 36, B622–B639 (2014).

    Article  MathSciNet  Google Scholar 

  30. Taylor, G. K., Nudds, R. L. & Thomas, A. L. R. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 425, 707–711 (2003).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank the Swiss National Science Foundation, and the MacArthur Foundation for partial financial support. We also thank W. van Rees, B. Hejazialhosseini and P. Koumoutsakos of the CSElab at ETH Zurich for their help with the computational aspects of the study, and Margherita Gazzola for her sketches.

Author information

Authors and Affiliations

  1. School of Engineering and Applied Sciences, Harvard University, Cambridge, Massachusetts 02138, USA

    Mattia Gazzola & L. Mahadevan

  2. Université Nice Sophia-Antipolis, Institut non linéaire de Nice, CNRS UMR 7335, 1361 route des lucioles, 06560 Valbonne, France

    Médéric Argentina

  3. Institut Universitaire de France, 103, boulevard Saint-Michel, 75005 Paris, France

    Médéric Argentina

  4. Department of Organismic and Evolutionary Biology, Department of Physics, Wyss Institute for Biologically Inspired Engineering, Kavli Institute for Nanobio Science and Technology, Harvard University, Cambridge, Massachusetts 02138, USA

    L. Mahadevan

Authors
  1. Mattia Gazzola
    View author publications

    Search author on:PubMed Google Scholar

  2. Médéric Argentina
    View author publications

    Search author on:PubMed Google Scholar

  3. L. Mahadevan
    View author publications

    Search author on:PubMed Google Scholar

Contributions

M.G., M.A. and L.M. conceived the study, developed the theory, collected and analysed the experimental data and wrote the paper. M.G. performed the 2D numerical simulations.

Corresponding authors

Correspondence to Mattia Gazzola or L. Mahadevan.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 4117 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gazzola, M., Argentina, M. & Mahadevan, L. Scaling macroscopic aquatic locomotion. Nature Phys 10, 758–761 (2014). https://doi.org/10.1038/nphys3078

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys3078

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics