Abstract
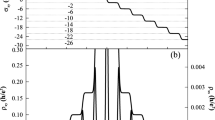
The energy spectrum of a two-dimensional electron gas placed in a transversal magnetic field B consists of quantized Landau levels. In the absence of disorder, the degeneracy of each Landau level is N=B A/φ0, where A is the area of the sample and φ0=h/e is the magnetic flux quantum. With disorder, localized states appear at the top and bottom of the broadened Landau level, whereas states in the centre of the Landau level (the critical region) remain delocalized. This single-electron theory adequately explains most aspects of the integer quantum Hall effect1. One unnoticed issue is the location of the new states that appear in the Landau level with increasing B. Here, we show that they appear predominantly inside the critical region. This situation leads to a ‘spectral ordering’ of the localized states, which explains the stripes observed in measurements of the local inverse compressibility2,3, of two-terminal conductance4 and of Hall and longitudinal resistances5 without the need to invoke interactions as done in previous work6,7,8.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to the full article PDF.
USD 39.95
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Klitzing, K. v., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).
Ilani, S. et al. The microscopic nature of localization in the quantum Hall effect. Nature 427, 328–332 (2004).
Martin, J. et al. Localization of fractionally charged quasi-particles. Science 305, 980–983 (2004).
Cobden, D. H., Barnes, C. H. W. & Ford, C. J. B. Fluctuations and evidence for charging in the quantum Hall effect. Phys. Rev. Lett. 82, 4695–4698 (1999).
Jouault, B. et al. Landau levels analysis by using symmetry properties of mesoscopic Hall bars. Phys. Rev. B 76, 161302(R) (2007).
Pereira, A. L. C. & Chalker, J. T. Electrostatic theory for imaging experiments on local charges in quantum Hall systems. Physica E 31, 155–159 (2006).
Struck, A. & Kramer, B. Electron correlations and single-particle physics in the integer quantum Hall effect. Phys. Rev. Lett. 97, 106801 (2006).
Sohrmann, C. & Römer, R. A. Compressibility stripes for mesoscopic quantum Hall samples. New J. Phys. 9, 97–122 (2007).
Thouless, D. J. et al. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).
Huo, Y. & Bhatt, R. N. Current carrying states in the lowest Landau level. Phys. Rev. Lett. 68, 1375–1378 (1992).
Yang, K. & Bhatt, R. N. Current-carrying states in a random magnetic field. Phys. Rev. B 55, R1922–R1925 (1997).
Thouless, D. J. Wannier functions for magnetic sub-bands. J. Phys. C 17, L325–L327 (1984).
Pruisken, A. M. M. Universal singularities in the integral quantum Hall effect. Phys. Rev. Lett. 61, 1297 (1988).
Huckestein, B. Scaling theory of the integer quantum Hall effect. Rev. Mod. Phys. 67, 357–396 (1995).
Wei, H. P. et al. Experiments on delocalization and university in the integral quantum Hall effect. Phys. Rev. Lett. 61, 1294–1296 (1988).
Středa, P. Theory of quantised Hall conductivity in two dimensions. J. Phys. C 15, L717–L721 (1982).
Chang, M.-C. & Niu, Q. Berry phase, hyperorbits, and the Hofstadter spectrum. Phys. Rev. Lett. 75, 1348–1351 (1995).
Chang, M.-C. & Niu, Q. Berry phase, hyperorbits, and the Hofstadter spectrum: Semiclassical dynamics in magnetic Bloch bands. Phys. Rev. B 53, 7010–7023 (1985).
Yoo, M. J. et al. Scanning single-electron transistor microscopy: Imaging individual charges. Science 276, 579–582 (1997).
Zhitenev, N. B. et al. Imaging of localized electronic states in the quantum Hall regime. Nature 404, 473–476 (2000).
Zhou, C. & Berciu, M. Resistance fluctuations near integer quantum Hall transitions in mesoscopic samples. Europhys. Lett. 69, 602–608 (2005).
Zhou, C. & Berciu, M. Correlated mesoscopic fluctuations in integer quantum Hall transitions. Phys. Rev. B 72, 085306 (2005).
Jain, J. K. & Kivelson, S. A. Quantum Hall effect in quasi one-dimensional systems: Resistance fluctuations and breakdown. Phys. Rev. Lett. 60, 1542–1545 (1988).
Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).
Laughlin, R. B. Anomalous quantum Hall effect: An incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 50, 1395–1398 (1983).
Haldane, F. D. M. Fractional quantization of the Hall effect: A hierarchy of incompressible quantum fluid states. Phys. Rev. Lett. 51, 605–608 (1983).
Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989).
Acknowledgements
We thank B. Jouault and X.-G. Zhang for many stimulating discussions and insightful opinions. This research was carried out at the Center for Nanophase Materials Sciences, sponsored at Oak Ridge National Laboratory by the Division of Scientific User Facilities, US Department of Energy. M.B. acknowledges support from the Sloan Foundation, CIfAR Nanoelectronics and NSERC.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhou, C., Berciu, M. Spectral weight transfer in the integer quantum Hall effect and its consequences. Nature Phys 4, 24–27 (2008). https://doi.org/10.1038/nphys786
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/nphys786