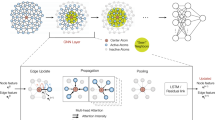
Abstract
The disordered nature of amorphous materials like metallic glasses has long hindered the establishment of well-defined structure-property relationships. Although it is widely recognized that short-range orders (SROs) within the first nearest-neighbor shell do not sufficiently characterize these materials, identifying the optimal characteristic length scale for capturing richer structural information remains elusive. Here, we resolve this ambiguity using a dual machine learning (ML) approach, which identifies the Radius of Informative Structural Environments (RISE) in a prototypical Zr-Cu metallic glass system. A top-down, reductionist approach, integrating SOAP descriptor with XGBoost model, demonstrates that the atomic environments within 5 Å radius entail maximal structural diversity and information density, leading to the optimal performance of the model on predicting given samples’ configurational energies. Concurrently, a bottom-up, emergentist Vision Transformer (ViT) architecture, designed to autonomously learn structural patterns from voxelized atomic configurations, shows that its predictive performance saturates when the effective communication length between its input patches reaches an equivalent spherical radius of ~5 Å. The striking convergence of these independent ML strategies provides compelling, data-driven evidence for the existence of an intrinsic, structurally informative length scale in metallic glasses. Additional robustness checks across multiple glassy materials with various elements numbers and bonding types confirm such RISE is not an artifact of encoding parameters or system size and aligns with existing experimental and computational insights.
Similar content being viewed by others
Data availability
The data supporting the findings of this study are available at https://zenodo.org/records/18066041.
Code availability
The code for the reductionist and emergentist models, including model training, is available at https://github.com/muchen1453/RISE.
References
Taylor, G. I. The mechanism of plastic deformation of crystals. Proc. R. Soc. Lond. A 145, 362–387 (1934).
Hall, E. O. The deformation and ageing of mild steel: III discussion of results. Proc. Phys. Soc. Sect. B 64, 747–753 (1951).
Petch, N. J. The cleavage strength of polycrystals. J. Iron Steel Inst. 174, 25–31 (1953).
Ding, J. et al. Universal structural parameter to quantitatively predict metallic glass properties. Nat. Commun. 7, 1–10 (2016).
Fan, Z. & Ma, E. Predicting orientation-dependent plastic susceptibility from static structure in amorphous solids via deep learning. Nat. Commun. 12, 1–13 (2021).
Ding, J. & Ma, E. Computational modeling sheds light on structural evolution in metallic glasses and supercooled liquids. npj Comput. Mater. 3, 1–12 (2017).
Wang, Q., Zhang, L. F., Zhou, Z. Y. & Yu, H. Bin. Predicting the pathways of string-like motions in metallic glasses via path-featurizing graph neural networks. Sci. Adv. 10, 2799 (2024).
Ren, F. et al. Accelerated discovery of metallic glasses through iteration of machine learning and high-throughput experiments. Sci. Adv. 4, eaaq1566 (2018).
Teich, E. G., Galloway, K. L., Arratia, P. E. & Bassett, D. S. Crystalline shielding mitigates structural rearrangement and localizes memory in jammed systems under oscillatory shear. Sci. Adv. 7, 3392–3404 (2021).
Cheng, Y. Q. & Ma, E. Atomic-level structure and structure–property relationship in metallic glasses. Prog. Mater. Sci. 56, 379–473 (2011).
Fan, Y., Iwashita, T. & Egami, T. Energy landscape-driven non-equilibrium evolution of inherent structure in disordered material. Nat. Commun. 8, 1–7 (2017).
Liu, C., Guan, P. & Fan, Y. Correlating defects density in metallic glasses with the distribution of inherent structures in potential energy landscape. Acta Mater. 161, 295–301 (2018).
Ma, E. Tuning order in disorder. Nat. Mater. 14, 547–552 (2015).
Sheng, H. W., Luo, W. K., Alamgir, F. M., Bai, J. M. & Ma, E. Atomic packing and short-to-medium-range order in metallic glasses. Nature 439, 419–425 (2006).
Wu, Y. et al. Substantially enhanced plasticity of bulk metallic glasses by densifying local atomic packing. Nat. Commun. 12, 1–9 (2021).
Cao, Y. et al. Continuous polyamorphic transition in high-entropy metallic glass. Nat. Commun. 15, 1–9 (2024).
Maldonis, J. J., Banadaki, A. D., Patala, S. & Voyles, P. M. Short-range order structure motifs learned from an atomistic model of a Zr50Cu45Al5 metallic glass. Acta Mater. 175, 35–45 (2019).
Fan, Z., Ding, J. & Ma, E. Machine learning bridges local static structure with multiple properties in metallic glasses. Mater. Today 40, 48–62 (2020).
Liu, C. et al. Concurrent prediction of metallic glasses’ global energy and internal structural heterogeneity by interpretable machine learning. Acta Mater. 259, 119281 (2023).
Wang, Q. & Jain, A. A transferable machine-learning framework linking interstice distribution and plastic heterogeneity in metallic glasses. Nat. Commun. 10, 1–11 (2019).
Luo, S., Khong, J. C., Huang, S., Yang, G. & Mi, J. Revealing in situ stress-induced short- and medium-range atomic structure evolution in a multicomponent metallic glassy alloy. Acta Mater. 272, 119917 (2024).
Zhao, P., Li, J., Hwang, J. & Wang, Y. Influence of nanoscale structural heterogeneity on shear banding in metallic glasses. Acta Mater. 134, 104–115 (2017).
Miyazaki, N., Wakeda, M., Wang, Y. J. & Ogata, S. Prediction of pressure-promoted thermal rejuvenation in metallic glasses. npj Comput. Mater. 2, 1–9 (2016).
Wang, Q. et al. Predicting the propensity for thermally activated β events in metallic glasses via interpretable machine learning. npj Comput. Mater. 6, 1–12 (2020).
Wang, Q. & Zhang, L. Inverse design of glass structure with deep graph neural networks. Nat. Commun. 12, 1–11 (2021).
Hilke, S. et al. The influence of deformation on the medium-range order of a Zr-based bulk metallic glass characterized by variable resolution fluctuation electron microscopy. Acta Mater. 171, 275–281 (2019).
Nomoto, K. et al. Medium-range order dictates local hardness in bulk metallic glasses. Mater. Today 44, 48–57 (2021).
Lee, M., Lee, C. M., Lee, K. R., Ma, E. & Lee, J. C. Networked interpenetrating connections of icosahedra: Effects on shear transformations in metallic glass. Acta Mater. 59, 159–170 (2011).
Wang, J. et al. Clustering-mediated enhancement of glass-forming ability and plasticity in oxygen-minor-alloyed Zr-Cu metallic glasses. Acta Mater. 261, 119386 (2023).
Tang, L. et al. Short- and medium-range orders in Al90Tb10 glass and their relation to the structures of competing crystalline phases. Acta Mater. 204, 116513 (2021).
Fang, X. W. et al. Spatially resolved distribution function and the medium-range order in metallic liquid and glass. Sci. Rep. 1, 1–5 (2011).
Laws, K. J., Miracle, D. B. & Ferry, M. A predictive structural model for bulk metallic glasses. Nat. Commun. 6, 1–10 (2015).
Wang, Q., Li, J. H., Liu, J. B. & Liu, B. X. Atomistic design of favored compositions for synthesizing the Al-Ni-Y metallic glasses. Sci. Rep. 5, 1–13 (2015).
Egami, T. & Ryu, C. W. Origin of medium-range atomic correlation in simple liquids: density wave theory. AIP Adv. 13, 85308 (2023).
Ryu, C. W., Dmowski, W. & Egami, T. Ideality of liquid structure: a case study for metallic alloy liquids. Phys. Rev. E 101, 030601 (2020).
Im, S. et al. Direct determination of structural heterogeneity in metallic glasses using four-dimensional scanning transmission electron microscopy. Ultramicroscopy 195, 189–193 (2018).
Deng, J. W., Du, K. & Sui, M. L. Medium range order of bulk metallic glasses determined by variable resolution fluctuation electron microscopy. Micron 43, 827–831 (2012).
Hwang, J. & Voyles, P. M. Variable resolution fluctuation electron microscopy on Cu-Zr metallic glass using a wide range of coherent STEM probe size. Microsc. Microanal. 17, 67–74 (2011).
Cubuk, E. D. et al. Identifying structural flow defects in disordered solids using machine-learning methods. Phys. Rev. Lett. 114, 108001 (2015).
Li, B. et al. Superior mechanical properties of a Zr-based bulk metallic glass via laser powder bed fusion process control. Acta Mater. 266, 119685 (2024).
Costa, M. B. & Greer, A. L. Enthalpy of anelasticity and rejuvenation of metallic glasses. Acta Mater. 265, 119609 (2024).
Wang, W. H. The elastic properties, elastic models and elastic perspectives of metallic glasses. Prog. Mater. Sci. 57, 487–656 (2012).
Wang, W. H., Dong, C. & Shek, C. H. Bulk metallic glasses. Mater. Sci. Eng. R Rep. 44, 45–89 (2004).
Greer, A. L., Cheng, Y. Q. & Ma, E. Shear bands in metallic glasses. Mater. Sci. Eng. R Rep. 74, 71–132 (2013).
De, S., Bartók, A. P., Csányi, G. & Ceriotti, M. Comparing molecules and solids across structural and alchemical space. Phys. Chem. Chem. Phys. 18, 13754–13769 (2016).
Chen, T. & Guestrin, C. XGBoost: a scalable tree boosting system. In Proc. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 785–794 (ACM, New York, NY, USA, 2016).
Dosovitskiy, A. et al. An image is worth 16x16 words: transformers for image recognition at scale. In Proc. ICLR 2021—9th International Conference on Learning Representations https://arxiv.org/pdf/2010.11929 (2020).
Piaggi, P. M. & Parrinello, M. Entropy based fingerprint for local crystalline order. J. Chem. Phys. 147, 114112 (2017).
Lundberg, S. M. & Lee, S.-I. A unified approach to interpreting model predictions. In Advances in Neural Information Processing Systems 30 4766–4775 (Curran Associates, Inc., Red Hook, NY, USA, 2017).
Sundararajan, M., Taly, A. & Yan, Q. Axiomatic attribution for deep networks. In Proc. 34th International Conference on Machine Learning 3319–3328 (JMLR.org, 2017).
Durandurdu, M. Ab initio modeling of metallic Pd80Si20 glass. Comput. Mater. Sci. 65, 44–47 (2012).
Yue, G. Q. et al. Local structure order in Pd78Cu6Si16 liquid. Sci. Rep. 5, 1–6 (2015).
Deringer, V. L. & Csányi, G. Machine learning based interatomic potential for amorphous carbon. Phys. Rev. B 95, 094203 (2017).
Deringer, V. L. et al. Realistic atomistic structure of amorphous silicon from machine-learning-driven molecular dynamics. J. Phys. Chem. Lett. 9, 2879–2885 (2018).
Abbasi, M. et al. In situ observation of medium range ordering and crystallization of amorphous TiO2 ultrathin films grown by atomic layer deposition. APL Mater. 11, 011102 (2023).
Meng, J. et al. Experimentally informed structure optimization of amorphous TiO2 films grown by atomic layer deposition. Nanoscale 15, 718–729 (2023).
Ma, D., Stoica, A. D. & Wang, X. L. Power-law scaling and fractal nature of medium-range order in metallic glasses. Nat. Mater. 8, 30–34 (2009).
Wu, Z. W. et al. Critical scaling of icosahedral medium-range order in CuZr metallic glass-forming liquids. Sci. Rep. 6, 1–7 (2016).
Hu, Y. C. & Tanaka, H. Unveiling hidden particle-level defects in glasses. Nat. Commun. 16, 5321 (2025).
Edelsbrunner, H., Letscher, D. & Zomorodian, A. Topological persistence and simplification. Discret. Comput. Geom. 28, 511–533 (2002).
Hiraoka, Y. et al. Hierarchical structures of amorphous solids characterized by persistent homology. Proc. Natl. Acad. Sci. USA 113, 7035–7040 (2016).
Liu, S. et al. Turing pattern and chemical medium-range order of metallic glasses. Mater. Today Phys. 38, 101254 (2023).
Zheng, S. et al. Active phase discovery in heterogeneous catalysis via topology-guided sampling and machine learning. Nat. Commun. 16, 1–13 (2025).
Townsend, J., Micucci, C. P., Hymel, J. H., Maroulas, V. & Vogiatzis, K. D. Representation of molecular structures with persistent homology for machine learning applications in chemistry. Nat. Commun. 11, 1–9 (2020).
Strudel, R., Garcia, R., Laptev, I. & Schmid, C. Segmenter: Transformer for Semantic Segmentation. In Proc. IEEE International Conference on Computer Vision 7242–7252. https://doi.org/10.1109/iccv48922.2021.00717 (2021).
Cheng, Y. Q., Ma, E. & Sheng, H. W. Atomic level structure in multicomponent bulk metallic glass. Phys. Rev. Lett. 102, 245501 (2009).
Liu, C. & Fan, Y. Emergent fractal energy landscape as the origin of stress-accelerated dynamics in amorphous solids. Phys. Rev. Lett. 127, 215502 (2021).
Acknowledgements
The authors acknowledge the support of NSF-DMR-2406530 (M.I., Yuchi Wang, Yunzhi Wang, J.H.) and NSF-DMR-2406531 (M.W., Yuchu Wang, Y.F.).
Author information
Authors and Affiliations
Contributions
M. W.: writing—original draft, visualization, methodology, investigation, formal analysis, data curation; Y. W.: methodology, formal analysis, data curation; M. I.: writing—review and editing; Y. W.: writing—review and editing; Y. W.: writing—review and editing, writing—original draft, resources, conceptualization; J. H.: writing—review and editing, writing—original draft, resources, conceptualization; Y. F.: writing—review and editing, writing—original draft, supervision, resources, investigation, conceptualization.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, M., Wang, Y., Islam, M. et al. Dual machine learning pinpoints the Radius of Informative Structural Environments in metallic glasses. npj Comput Mater (2026). https://doi.org/10.1038/s41524-026-01997-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-026-01997-z