Abstract
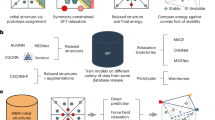
We present a machine learning-accelerated high-throughput (HTP) workflow for the discovery of functional materials. As a test case, quaternary and all-d Heusler compounds were screened for stable compounds with large magnetocrystalline anisotropy energy (Eaniso). Structure optimization and evaluation of formation energy and energy above the convex hull were performed using the eSEN-30M-OAM interatomic potential, while local magnetic moments, phonon stability, magnetic stability, and Eaniso were predicted by eSEN models trained on our DxMag Heusler database. A frozen transfer learning strategy was employed to improve accuracy. Candidate compounds identified by the ML-HTP workflow were validated with density functional theory, confirming high predictive precision. We also benchmark the performance of different uMLIPs, discuss the fidelity of local magnetic moment prediction, and demonstrate generalization to unseen elements via transfer learning from a universal interatomic potential.
Similar content being viewed by others
Data availability
The ML-HTP candidate list and DFT validation results are included in the Supplementary Information as Tables S3 and S4. The complete set of all screened compounds, along with ML-predicted properties, will be made available through the HeuslerDB database at https://www.nims.go.jp/group/spintheory/.
Code availability
The developed packages MLIP-HOT and MLIP-FTL will be made available through the Spin Theory Group GitHub repository at https://github.com/nims-spin-theory and our group website at https://www.nims.go.jp/group/spintheory/.
References
Sanvito, S. et al. Accelerated discovery of new magnets in the Heusler alloy family. Sci. Adv. 3, e1602241 (2017).
Zhang, H. High-throughput design of magnetic materials. Electron. Struct. 3, 033001 (2021).
Barwal, V. et al. Large magnetoresistance and high spin-transfer torque efficiency of Co2MnxFe1−xGe (0 ≤ x ≤ 1) Heusler alloy thin films obtained by high-throughput compositional optimization using combinatorially sputtered composition-gradient film. APL Mater. 12, 111114 (2024).
Faleev, S. V. et al. Heusler compounds with perpendicular magnetic anisotropy and large tunneling magnetoresistance. Phys. Rev. Mater. 1, 024402 (2017).
Hu, K. et al. High-throughput design of Co-based magnetic Heusler compounds. Acta Mater. 259, 119255 (2023).
Hilgers, R., Wortmann, D. & Blügel, S. Machine Learning-based estimation and explainable artificial intelligence-supported interpretation of the critical temperature from magnetic ab initio Heusler alloys data. Phys. Rev. Mater. 9, 044412 (2025).
Baigutlin, D. R., Sokolovskiy, V. V., Buchelnikov, V. D. & Taskaev, S. V. Machine learning algorithms for optimization of magnetocaloric effect in all-d-metal Heusler alloys. J. Appl. Phys. 136, 183903 (2024).
Mitra, S., Ahmad, A., Biswas, S. & Kumar Das, A. A machine learning approach to predict the structural and magnetic properties of Heusler alloy families. Comput. Mater. Sci. 216, 111836 (2023).
Liu, C. et al. Machine learning to predict quasicrystals from chemical compositions. Adv. Mater. 33, 2102507 (2021).
Xie, R., Crivello, J.-C. & Barreteau, C. Screening new quaternary semiconductor Heusler compounds by machine-learning methods. Chem. Mater. 35, 7615–7627 (2023).
Lu, Y., Sun, Y., Hou, C., Li, Z. & Ni, J. Explainable attention CNN for predicting properties of Heusler alloys. J. Phys. Chem. C 129, 14958–14967 (2025).
Xie, T. & Grossman, J. C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120, 145301 (2018).
Choudhary, K. & DeCost, B. Atomistic line graph neural network for improved materials property predictions. npj Comput. Mater. 7, 1–8 (2021).
Barroso-Luque, L. et al. Open materials 2024 (OMat24) inorganic materials dataset and models.Preprint at arXiv https://doi.org/10.48550/arXiv.2410.12771 (2024).
Yamada, H. et al. Predicting materials properties with little data using shotgun transfer learning. ACS Cent. Sci. 5, 1717–1730 (2019).
Lee, J. & Asahi, R. Transfer learning for materials informatics using crystal graph convolutional neural network. Comput. Mater. Sci. 190, 110314 (2021).
Hoffmann, N., Schmidt, J., Botti, S. & Marques, M. A. L. Transfer learning on large datasets for the accurate prediction of material properties. Digit. Discov. 2, 1368–1379 (2023).
He, J., Rabe, K. M. & Wolverton, C. Computationally accelerated discovery of functional and structural Heusler materials. MRS Bull. 47, 559–572 (2022).
Noky, J., Zhang, Y., Gooth, J., Felser, C. & Sun, Y. Giant anomalous Hall and Nernst effect in magnetic cubic Heusler compounds. npj Comput. Mater. 6, 1–8 (2020).
Xing, G., Masuda, K., Tadano, T. & Miura, Y. Chemical-substitution-driven giant anomalous Hall and Nernst effects in magnetic cubic Heusler compounds. Acta Mater. 270, 119856 (2024).
Xiao, E. & Tadano, T. High-throughput computational screening of Heusler compounds with phonon considerations for enhanced material discovery. Acta Mater. 297, 121312 (2025).
Xie, Y., Tritsaris, G. A., Grånäs, O. & Rhone, T. D. Data-driven studies of the magnetic anisotropy of two-dimensional magnetic materials. J. Phys. Chem. Lett. 12, 12048–12054 (2021).
Liao, T. et al. Predicting magnetic anisotropy energies using site-specific spin-orbit coupling energies and machine learning: application to iron-cobalt nitrides. Phys. Rev. Mater. 6, 024402 (2022).
Dutta, A. & Sen, P. Machine learning assisted hierarchical filtering: a strategy for designing magnets with large moment and anisotropy energy 10, 3404–3417 (2022).
Fu, X. et al. Learning smooth and expressive interatomic potentials for physical property prediction. Proc. Mach. Learn. Res. 267, 17875–17893 (2025)..
Choudhary, K. et al. Unified graph neural network force-field for the periodic table: Solid state applications. Digit. Discov. 2, 346–355 (2023).
Deng, B. et al. CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling. Nat. Mach. Intell. 5, 1031–1041 (2023).
Kim, J. et al. Data-efficient multifidelity training for high-fidelity machine learning interatomic potentials. J. Am. Chem. Soc. 147, 1042–1054 (2025).
Yan, K. et al. A materials foundation model via hybrid invariant-equivariant architectures. Preprint at arXiv https://doi.org/10.48550/arXiv.2503.05771 (2025).
Yang, H. et al. MatterSim: a deep learning atomistic model across elements, temperatures and pressures. Preprint at arXiv https://doi.org/10.48550/arXiv.2405.04967 (2024).
Hu, X. et al. Searching high spin polarization ferromagnet in Heusler alloy via machine learning. J. Phys. Condens. Matter 32, 205901 (2020).
Miyazaki, H. et al. Machine learning based prediction of lattice thermal conductivity for half-Heusler compounds using atomic information. Sci. Rep. 11, 13410 (2021).
Kim, K. et al. Machine-learning-accelerated high-throughput materials screening: Discovery of novel quaternary Heusler compounds. Phys. Rev. Mater. 2, 123801 (2018).
Liu, K. et al. Machine learning assisted development of Heusler alloys for high magnetic moment. Comput. Mater. Sci. 250, 113692 (2025).
Hirohata, A. et al. Machine learning for the development of new materials for a magnetic tunnel junction. npj Spintron. 3, 1–9 (2025).
Jain, A. et al. Commentary: The Materials Project: a materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013).
Schmidt, J. et al. Machine-learning-assisted determination of the global zero-temperature phase diagram of materials. Adv. Mater. 35, 2210788 (2023).
Schmidt, J. et al. Improving machine-learning models in materials science through large datasets. Mater. Today Phys. 48, 101560 (2024).
Kim, S. Y., Park, Y. J. & Li, J. Leveraging neural network interatomic potentials for a foundation model of chemistry (2025). https://doi.org/10.48550/arXiv.2506.18497 (2025).
Chen, C., Ye, W., Zuo, Y., Zheng, C. & Ong, S. P. Graph networks as a universal machine learning framework for molecules and crystals. Chem. Mater. 31, 3564–3572 (2019).
Chang, R., Wang, Y.-X. & Ertekin, E. Towards overcoming data scarcity in materials science: unifying models and datasets with a mixture of experts framework. npj Comput. Mater. 8, 242 (2022).
Minami, S. et al. Scaling law of Sim2Real transfer learning in expanding computational materials databases for real-world predictions. npj Comput. Mater. 11, 146 (2025).
Sun, W. et al. The thermodynamic scale of inorganic crystalline metastability. Sci. Adv. 2, e1600225 (2016).
Saal, J. E., Kirklin, S., Aykol, M., Meredig, B. & Wolverton, C. Materials design and discovery with high-throughput density functional theory: the open quantum materials database (OQMD). JOM 65, 1501–1509 (2013).
Bahn, S. & Jacobsen, K. An object-oriented scripting interface to a legacy electronic structure code. Comput. Sci. Eng. 4, 56–66 (2002).
Tadano, T. & Tsuneyuki, S. Self-consistent phonon calculations of lattice dynamical properties in cubic SrTiO3 with first-principles anharmonic force constants. Phys. Rev. B 92, 054301 (2015).
Tadano, T., Gohda, Y. & Tsuneyuki, S. Anharmonic force constants extracted from first-principles molecular dynamics: applications to heat transfer simulations. J. Phys.: Condens. Matter 26, 225402 (2014).
Ebert, H., Ködderitzsch, D. & Minár, J. Calculating condensed matter properties using the KKR-Green’s function method—recent developments and applications. Rep. Prog. Phys. 74, 096501 (2011).
Liechtenstein, A. I., Katsnelson, M. I., Antropov, V. P. & Gubanov, V. A. Local spin density functional approach to the theory of exchange interactions in ferromagnetic metals and alloys. J. Magn. Magn. Mater. 67, 65–74 (1987).
Hjorth Larsen, A. et al. The atomic simulation environment—a Python library for working with atoms. J. Phys. Condens. Matter 29, 273002 (2017).
Bitzek, E., Koskinen, P., Gähler, F., Moseler, M. & Gumbsch, P. Structural relaxation made simple. Phys. Rev. Lett. 97, 170201 (2006).
Chanussot, L. et al. Open Catalyst 2020 (OC20) dataset and community challenges. ACS Catal. 11, 6059–6072, https://doi.org/10.1021/acscatal.0c04525 (2021).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Daalderop, G. H. O., Kelly, P. J. & Schuurmans, M. F. H. First-principles calculation of the magnetocrystalline anisotropy energy of iron, cobalt, and nickel. Phys. Rev. B 41, 11919–11937 (1990).
Xing, G., Miura, Y. & Tadano, T. Lattice dynamics and its effects on magnetocrystalline anisotropy energy of pristine and hole-doped YCo5 from first principles. Phys. Rev. B 105, 104427 (2022).
Xing, G., Miura, Y. & Tadano, T. First-principles prediction of phase transition of YCo5 from self-consistent phonon calculations. Phys. Rev. B 108, 014304 (2023).
Ong, S. P. et al. Python materials genomics (pymatgen): a robust, open-source Python library for materials analysis. Comput. Mater. Sci. 68, 314–319 (2013).
Blöchl, P. E., Jepsen, O. & Andersen, O. K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 49, 16223–16233 (1994).
ASE2SPRKKR software package — ASE2SPRKKR documentation. https://ase2sprkkr.github.io/ase2sprkkr/.
Togo, A., Shinohara, K. & Tanaka, I. Spglib: a software library for crystal symmetry search. Sci. Technol. Adv. Mater. Methods 4, 2384822 (2024).
Acknowledgements
This study used computational resources of the supercomputer Fugaku provided by the RIKEN Center for Computational Science (Project ID: hp250229), the computer resources provided by ISSP, U-Tokyo under the program of SCCMS, and the computer resources at NIMS Numerical Materials Simulator. This study was supported by MEXT Program: Data Creation and Utilization-Type Material Research and Development Project (Digital Transformation Initiative Center for Magnetic Materials) Grant Number JPMXP1122715503 and as “Program for Promoting Researches on the Supercomputer Fugaku” (Data-Driven Research Methods Development and Materials Innovation Led by Computational Materials Science, JPMXP1020230327).
Author information
Authors and Affiliations
Contributions
T.T. conceptualized, designed, and supervised the project; reviewed and edited the manuscript. T.T. and E.X. developed the methodology and code implementation; performed the calculations and analysis; E.X. drafted the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xiao, E., Tadano, T. Accurate screening of functional materials with machine-learning potential and transfer-learned regressions: Heusler alloy benchmark. npj Comput Mater (2026). https://doi.org/10.1038/s41524-026-02013-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-026-02013-0