Abstract
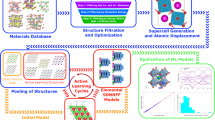
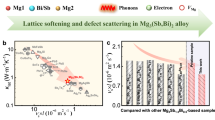
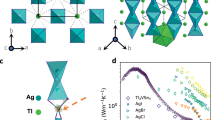
Pushing the intrinsic lattice thermal conductivity (LTC) in crystalline materials to lower bounds is crucial for fundamental materials research towards emerging technologies including thermoelectric energy conversion and thermal management in both hypersonic aircraft and next-generation turbine systems. However, in the ultralow LTC regime ( < 1 Wm-1K-1), the competition between propagative (particle-like) and coherent phonons—arising from off-diagonal components—poses a significant challenge in further reducing LTC. We perform quantitative analysis of 4700 materials using density functional theory (DFT), spanning all crystallographic groups, to elucidate the interplay between diagonal and off-diagonal phonon contributions. We identify a critical balance between these transport mechanisms, where intermediate phonon lifetimes ( ~ 1 ps) and slow group velocities ( ~ 1 km/s) collectively suppress both contributions, enabling ultralow LTC. Results from a large dataset of 31,058 structures by machine learning models strongly resemble the DFT trends of two-channel phonon transport. Leveraging these models, we screen 25,882 additional materials and confirm their properties with DFT, identifying 12 candidates with ultralow room-temperature LTC—including a record-low value of 0.132 Wm-1K-1. Our large-scale analysis reveals fundamental insights into dual-channel phonon transport, enabling rational design of ultralow LTC materials and accelerating the discovery of advanced phononic crystals with tailored thermal transport properties.
Similar content being viewed by others
Data availability
The DFT dataset containing 4700 structures used to train the ALIGNN models as well as the ALIGNN predicted phonon properties of 31,225 structures are shared in the supporting Excel files. The atomic structures with relevant structure information are provided in CIF format embedded in the Excel files. All data reported herein are available upon reasonable request to the corresponding author.
References
Ghosh, T., Dutta, M., Sarkar, D. & Biswas, K. Insights into low thermal conductivity in inorganic materials for thermoelectrics. J. Am. Chem. Soc. 144, 10099–10118 (2022).
Jiang, Y. et al. Suppressing electron-phonon coupling in organic photovoltaics for high-efficiency power conversion. Nat Commun 14, (2023).
Lindsay, L., Katre, A., Cepellotti, A. & Mingo, N. Perspective on ab initio phonon thermal transport. J. Appl Phys. 126, 1–20 (2019).
Allen, P. B. & Feldman, J. L. Thermal conductivity of glasses: theory and application to amorphous Si. Phys. Rev. Lett. 62, 645–648 (1989).
Hanus, R. et al. Thermal transport in defective and disordered materials. Appl. Phys. Rev https://doi.org/10.1063/5.0055593 (2021).
McGaughey, A. J. H., Jain, A., Kim, H. Y. & Fu, B. Phonon properties and thermal conductivity from first principles, lattice dynamics, and the Boltzmann transport equation. J. Appl. Phys. 125, (2019).
Ma, T., Chakraborty, P., Guo, X., Cao, L. & Wang, Y. First-Principles Modeling of Thermal Transport in Materials: Achievements, Opportunities, and Challenges. International Journal of Thermophysics vol. 41 (Springer US, 2020).
Simoncelli, M., Marzari, N. & Mauri, F. Unified theory of thermal transport in crystals and glasses. Nat. Phys. 15, 809–813 (2019).
Agne, M. T., Hanus, R. & Snyder, G. J. Minimum thermal conductivity in the context of diffuson-mediated thermal transport. Energy Environ. Sci. 11, 609–616 (2018).
Hanus, R. et al. Uncovering design principles for amorphous-like heat conduction using two-channel lattice dynamics. Materials Today Physics 18, (2021).
Xia, Y. et al. A unified understanding of minimum lattice thermal conductivity. Proceedings of the National Academy of Sciences 120, (2023).
Zeng, Z. et al. Pushing thermal conductivity to its lower limit in crystals with simple structures. Nat Commun 15, (2024).
Ojih, J. et al. High-throughput computational discovery of 3218 ultralow thermal conductivity and dynamically stable materials by dual machine learning models. J. Mater. Chem. A Mater. 11, 24169–24183 (2023).
Rodriguez, A. et al. Unlocking phonon properties of a large and diverse set of cubic crystals by indirect bottom-up machine learning approach. Commun Mater 4, (2023).
Jain, A., Veeravenkata, H. P., Godse, S. & Srivastava, Y. High-throughput computational discovery of 40 ultralow thermal conductivity and 20 highly anisotropic crystalline materials. ArXiv http://arxiv.org/abs/2204.03628 (2022).
Rodriguez, A. et al. Million-scale data integrated deep neural network for phonon properties of heuslers spanning the periodic table. NPJ Comput Mater 9, (2023).
Petretto, G. et al. High-throughput density-functional perturbation theory phonons for inorganic materials. Sci Data 5, (2018).
Mukherjee, M., Srivastava, A. & Singh, A. K. Recent advances in designing thermoelectric materials. J. Mater. Chem C https://doi.org/10.1039/d2tc02448a (2022).
Bhui, A. et al. Intrinsically low thermal conductivity in the n-type vacancy-ordered double perovskite cs2sni6: octahedral rotation and anharmonic rattling. Chem. Mater. 34, 3301–3310 (2022).
Ohnishi, M. et al. Database and Deep-Learning Scalability of Anharmonic Phonon Properties by Automated Brute-Force First-Principles Calculations.
Lee, W. et al. Ultralow thermal conductivity in all-inorganic halide perovskites. Proc. Natl. Acad. Sci. USA 114, 8693–8697 (2017).
Mukhopadhyay, S. et al. Two-channel model for ultralow thermal conductivity of crystalline Tl3VSe4. Science (1979) 360, 1455–1458 (2018).
Zhu, Z. et al. A high-throughput framework for lattice dynamics. NPJ Comput Mater 10, (2024).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015).
Li, W., Carrete, J., Katcho, N. A. & Mingo, N. ShengBTE: A solver of the Boltzmann transport equation for phonons. Comput Phys. Commun. 185, 1747–1758 (2014).
Ojih, J. et al. Machine learning accelerated discovery of promising thermal energy storage materials with high heat capacity. ACS Appl Mater. Interfaces 14, 43277–43289 (2022).
Yang, X., Feng, T., Li, J. & Ruan, X. Stronger role of four-phonon scattering than three-phonon scattering in thermal conductivity of III-V semiconductors at room temperature. Phys Rev B 100, (2019).
Li, S. et al. High thermal conductivity in cubic boron arsenide crystals. Science (1979) 361, 579–581 (2018).
Xia, Y. et al. High-throughput study of lattice thermal conductivity in binary rocksalt and zinc blende compounds including higher-order anharmonicity. Phys. Rev. X 10, 41029 (2020).
Sun, J. et al. Four-phonon scattering effect and two-channel thermal transport in two-dimensional paraelectric SnSe. ACS Appl Mater. Interfaces 14, 11493–11499 (2022).
Simoncelli, M., Marzari, N. & Mauri, F. Wigner formulation of thermal transport in solids. Phys. Rev. X 12, 41011 (2022).
Choudhary, K. & DeCost, B. Atomistic Line Graph Neural Network for improved materials property predictions. NPJ Comput Mater 7, (2021).
Breiman, L. Random Forests. Mach. Learn 45, 5–32 (2001).
Chen, T. & Guestrin, C. XGBoost: A scalable tree boosting system. in Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining vols 13-17-August-2016 785–794 (Association for Computing Machinery, 2016).
Ke, G. et al. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. in 31st International Conference on Neural Information Processing Systems 3149–3157 (Curran Associates Inc., Red Hook, NY, 2017).
Hoerl, A. E. & Kennard, R. W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 12, 55 (1970).
Liu, P.-F. et al. Strong low-energy rattling modes enabled liquid-like ultralow thermal conductivity in a well-ordered solid. Natl Sci Rev 11, (2024).
Pal, K., Xia, Y. & Wolverton, C. Microscopic mechanism of unusual lattice thermal transport in TlInTe2. NPJ Comput Mater 7, (2021).
Osei-Agyemang, E., Adu, C. E. & Balasubramanian, G. Ultralow lattice thermal conductivity of chalcogenide perovskite CaZrSe3 contributes to high thermoelectric figure of merit. NPJ Comput Mater 5, (2019).
Acknowledgements
This work was supported by the NSF (award number 2030128, 2110033, 2311202, 2320292) and supported in part by ADAPT in SC and SC EPSCoR (Grant No. 24-GC02). ADAPT in SC is funded by the NSF under award number OIA-2242812. R.R. acknowledges financial support by the Severo Ochoa Centres of Excellence Program under grant CEX2023-001263-S, and by the Agencia Estatal de Investigación under grant PID2024-162811NB-I00. Calculations were performed at Theia, an AI-focused HPC cluster at the University of South Carolina supported by NSF (award number 2320292), and at the Centro de Supercomputación de Galicia (CESGA) and at the Barcelona Supercomputing Center (BSC) within actions FI-2024-1-0012, FI-2024-2-0015, FI-2025-1-0010, and FI-2025-2-0015 of the Red Española de Supercomputación (RES).
Author information
Authors and Affiliations
Contributions
M.H. conveyed the idea and designed and supervised the study. G.J.S. provided fruitful discussion and insights into the problem. R.R. performed partial DFT calculations. A.R. performed the off-diagonal calculations. C.L. wrote the CSLD code for IFC fitting. J.O. and M.A. participated in establishing workflow and processing data. A.R. prepared the draft of the manuscript. R.R., G.J.S. and M.H. revised the manuscript. All authors contributed to discussions and interpretation of results in the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Rodriguez, A., Rurali, R., Lin, C. et al. Approaching lower bound of lattice thermal conductivity by simultaneously suppressing diagonal and off-diagonal phonon contributions. npj Comput Mater (2026). https://doi.org/10.1038/s41524-026-02018-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-026-02018-9