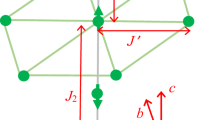
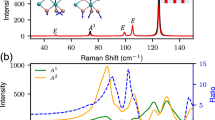
Abstract
Lattice vibrations are highly sensitive to crystal symmetries and their changes across phase transitions. The latter can modify irreducible (co)representations and corresponding infrared and Raman selection rules of phonons. This concept is established for relativistic magnetic point groups, simultaneously transforming spatial and spin coordinates. However, in altermagnets described by non-relativistic spin groups with disjunct symmetry operations for both vector spaces, the phonon selection rules have remained unexplored. Here, we present a detailed study of the infrared- and Raman-active modes in the collinear antiferromagnet and altermagnet candidate Co2Mo3O8. Comparing to ab initio calculations accurately capturing the eigenfrequencies, we identify all expected phonon modes at room temperature and deduce their selection rules using both symmetry approaches. Importantly, we observe the change of selection rules upon antiferromagnetic ordering, agreeing with the relativistic symmetry approach, while the spin group formalism predicts no changes. Therefore, optical phonons sensing the symmetry of the magnetic order can reveal if relevant magnon-phonon coupling is compatible with the spin-group approach or not.
Similar content being viewed by others
Data availability
The IR, Raman, and THz spectra are available on Zenodo https://doi.org/10.5281/zenodo.17663262.
References
Šmejkal, L., Sinova, J. & Jungwirth, T. Beyond conventional ferromagnetism and antiferromagnetism: a phase with nonrelativistic spin and crystal rotation symmetry. Phys. Rev. X 12, 031042 (2022).
Bhowal, S. & Spaldin, N. A. Ferroically ordered magnetic octupoles in d-wave altermagnets. Phys. Rev. X 14, 011019 (2024).
Morano, V. C. et al. Absence of altermagnetic magnon band splitting in MnF2. Phys. Rev. Lett. 134, 226702 (2025).
Yu, B.-W. & Liu, B.-G. Spin-split flat bands at the band edge and two-dimensional hole gases towards quantum Hall effect in altermagnetic CoF2. Preprint at https://arxiv.org/abs/2411.16188 (2024).
Dubrovin, R. M. et al. Polar phonons and magnetic excitations in the antiferromagnet CoF2. Phys. Rev. B 109, 224312 (2024).
Lee, S. et al. Broken Kramers degeneracy in altermagnetic MnTe. Phys. Rev. Lett. 132, 036702 (2024).
Krempaský, J. et al. Altermagnetic lifting of Kramers spin degeneracy. Nature 626, 517 (2024).
Liu, Z., Ozeki, M., Asai, S., Itoh, S. & Masuda, T. Chiral split magnon in altermagnetic MnTe. Phys. Rev. Lett. 133, 156702 (2024).
Jost, D. et al. Chiral altermagnon in MnTe. Preprint at https://arxiv.org/abs/2501.17380 (2025).
Fedchenko, O. et al. Observation of time-reversal symmetry breaking in the band structure of altermagnetic RuO2. Sci. Adv. 10, adj4883 (2024).
Wenzel, M. et al. Fermi-liquid behavior of nonaltermagnetic RuO2. Phys. Rev. B 111, l041115 (2025).
Liu, J. et al. Absence of altermagnetic spin splitting character in rutile oxide RuO2. Phys. Rev. Lett. 133, 176401 (2024).
Naish, V. E. On magnetic symmetry of crystals. Izv. Akad. Nauk SSSR 27, 1496 (1963).
Brinkman, W. F. & Elliott, R. J. Theory of spin-space groups. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 294, 343 (1966).
Litvin, D. & Opechowski, W. Spin groups. Physica 76, 538 (1974).
Litvin, D. B. Spin point groups. Acta Crystallogr. Sect. A 33, 279 (1977).
Bradley, C. J. & Cracknell, A. P. The Mathematical Theory Of Symmetry In Solids: Representation theory for point groups and space groups (Oxford University PressOxford, 2009). https://doi.org/10.1093/oso/9780199582587.001.0001.
Kurumaji, T., Ishiwata, S. & Tokura, Y. Doping-tunable ferrimagnetic phase with large linear magnetoelectric effect in a polar magnet Fe2Mo3O8. Phys. Rev. X 5, 031034 (2015).
Wang, Y. et al. Unveiling hidden ferrimagnetism and giant magnetoelectricity in polar magnet Fe2Mo3O8. Sci. Rep. 5, 12268 (2015).
Kurumaji, T., Ishiwata, S. & Tokura, Y. Diagonal magnetoelectric susceptibility and effect of Fe doping in the polar ferrimagnet Mn2Mo3O8. Phys. Rev. B 95, 045142 (2017).
Tang, Y. S. et al. Collinear magnetic structure and multiferroicity in the polar magnet Co2Mo3O8. Phys. Rev. B 100, 134112 (2019).
Csizi, B. et al. Magnetic and vibronic terahertz excitations in Zn-doped Fe2Mo3O8. Phys. Rev. B 102, 174407 (2020).
Tang, Y. S. et al. Metamagnetic transitions and magnetoelectricity in the spin-1 honeycomb antiferromagnet Ni2Mo3O8. Phys. Rev. B 103, 014112 (2021).
Tang, Y. S. et al. Successive electric polarization transitions induced by high magnetic field in the single-crystal antiferromagnet Co2Mo3O8. Phys. Rev. B 105, 064108 (2022).
Reschke, S. et al. Confirming the trilinear form of the optical magnetoelectric effect in the polar honeycomb antiferromagnet Co2Mo3O8. npj Quantum Mater. 7, 1 (2022).
Prodan, L. et al. Dilution of a polar magnet: structure and magnetism of Zn-substituted Co2Mo3O8. Phys. Rev. B 106, 174421 (2022).
Ghara, S. et al. Magnetization reversal through an antiferromagnetic state. Nat. Commun. 14, 5174 (2023).
Szaller, D. et al. Coexistence of antiferromagnetism and ferrimagnetism in adjacent honeycomb layers. Phys. Rev. B 111, 184404 (2025).
Kurumaji, T. et al. Electromagnon resonance in a collinear spin state of the polar antiferromagnet Fe2Mo3O8. Phys. Rev. B 95, 020405(R) (2017).
Wu, F. et al. Fluctuation-enhanced phonon magnetic moments in a polar antiferromagnet. Nat. Phys. 1868 https://doi.org/10.1038/s41567-023-02210-4 (2023).
Bao, S. et al. Direct observation of topological magnon polarons in a multiferroic material. Nat. Commun. 14, 6093 (2023).
Vasin, K. V. et al. Optical magnetoelectric effect in the polar honeycomb antiferromagnet Fe2Mo3O8. Phys. Rev. B 110, 054401 (2024).
Cheong, S.-W. & Huang, F.-T. Altermagnetism with non-collinear spins. npj Quantum Mater. 9, 13 (2024).
Chen, X. et al. Unconventional magnons in collinear magnets dictated by spin space groups. Nature 640, 349 (2025).
Varret, F., Czeskleba, H., Hartmann-Boutron, F. & Imbert, P. Étude par effet Mössbauer de lion Fe2+ en symétrie trigonale dans les composés du type (Fe, M)2Mo3O8 (M = Mg, Zn, Mn, Co, Ni) et propriétés magnétiques de (Fe, Zn)2Mo3O8. J. Phys. 33, 549 (1972).
Cotton, F. A. Metal atom clusters in oxide systems. Inorg. Chem. 3, 1217 (1964).
Reschke, S. et al. Structure, phonons, and orbital degrees of freedom in Fe2Mo3O8. Phys. Rev. B 102, 094307 (2020).
McClarty, P. A. & Rau, J. G. Landau theory of altermagnetism. Phys. Rev. Lett. 132, 176702 (2024).
Schiff, H., McClarty, P., Rau, J. G. & Romhányi, J. Collinear altermagnets and their Landau theories. Phys. Rev. Res. 7, 033301 (2025).
Stanislavchuk, T. N. et al. Spectroscopic and first principle DFT+eDMFT study of complex structural, electronic, and vibrational properties of M2Mo3O8 (M = Fe, Mn) polar magnets. Phys. Rev. B 102, 115139 (2020).
Cracknell, A. P. Scattering matrices for the Raman effect in magnetic crystals. J. Phys. C Solid State Phys. 2, 500 (1969).
Schiff, H., Corticelli, A., Guerreiro, A., Romhányi, J. & McClarty, P. A. The crystallographic spin point groups and their representations. SciPost Phys. 18, 109 (2025).
Jaeschke-Ubiergo, R., Bharadwaj, V. K., Jungwirth, T., Šmejkal, L. & Sinova, J. Supercell altermagnets. Phys. Rev. B 109, 094425 (2024).
Hayes, W. & Loudon, R. Scattering of Light by Crystals (Dover, 2004).
Manuel Cardona, G. G. ed. Light Scattering in Solids II (Springer Berlin Heidelberg, 1982) https://doi.org/10.1007/3-540-11380-0.
Shapiro, S. M. & Axe, J. D. Raman Scattering from Polar Phonons. Phys. Rev. B 6, 2420 (1972).
Ovander, L. N. & Tyu, N. S. Theory of Raman scattering on polar phonons. Phys. Status Solidi B 91, 763 (1979).
Martin, R. M. & Damen, T. C. Breakdown of selection rules in resonance Raman scattering. Phys. Rev. Lett. 26, 86 (1971).
Trallero-Giner, C., Cantarero, A. & Cardona, M. One-phonon resonant Raman scattering: Fröhlich exciton-phonon interaction. Phys. Rev. B 40, 4030 (1989).
Rikken, G. L. J. A., Strohm, C. & Wyder, P. Observation of magnetoelectric directional anisotropy. Phys. Rev. Lett. 89, 133005 (2002).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Acknowledgements
M.K. and K.P. thank Hana Schiff for stimulating discussions. This research was partly funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)-TRR 360-492547816. The support by 0.25 N within the project ANCD (cod 011201 Moldova) is also acknowledged. The authors gratefully acknowledge the use of computing resources of the ALCC HPC cluster (Institute of Physics, University of Augsburg). We acknowledge the support of the LNCMI-CNRS, member of the European Magnetic Field Laboratory (EMFL). This research was supported by the Ministry of Culture and Innovation and the National Research, Development and Innovation Office within the Quantum Information National Laboratory of Hungary (Grant No. 2022-2.1.1-NL-2022-00004) as well as the Hungarian NKFIH Grant No. K 142652 and FK135003. M.K. was partially funded by the scholarship program DKÖP-25-1-BME-25 of NKFIH and Budapest University of Technology and Economics.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
L.P. and V.T. synthesized and characterized the crystals; F.S., O.E., and K.V. measured the reflectivity and transmission spectra; D.U., A.P., C.F. and P.L. measured the Raman spectra; F.S., K.V., O.E. and J.D. analyzed the data; A.A.T. performed the ab initio calculations; M.K., K.P., S.B. and J.D. performed the group theoretical analysis; F.S., M.K., K.P., S.B. and J.D. wrote the paper; I.K., S.B. and J.D. planned and coordinated the project; All authors contributed to the discussion and interpretation of the experimental and theoretical results and to the completion of the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schilberth, F., Kondákor, M., Ukolov, D. et al. Optical phonons as a testing ground for spin group symmetries. npj Quantum Mater. (2026). https://doi.org/10.1038/s41535-026-00857-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-026-00857-9