The ergodicity problem in economics

Abstract

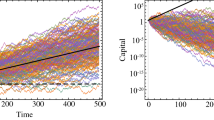
The ergodic hypothesis is a key analytical device of equilibrium statistical mechanics. It underlies the assumption that the time average and the expectation value of an observable are the same. Where it is valid, dynamical descriptions can often be replaced with much simpler probabilistic ones — time is essentially eliminated from the models. The conditions for validity are restrictive, even more so for non-equilibrium systems. Economics typically deals with systems far from equilibrium — specifically with models of growth. It may therefore come as a surprise to learn that the prevailing formulations of economic theory — expected utility theory and its descendants — make an indiscriminate assumption of ergodicity. This is largely because foundational concepts to do with risk and randomness originated in seventeenth-century economics, predating by some 200 years the concept of ergodicity, which arose in nineteenth-century physics. In this Perspective, I argue that by carefully addressing the question of ergodicity, many puzzles besetting the current economic formalism are resolved in a natural and empirically testable way.