Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Perspective
  • Published:

Topology shapes dynamics of higher-order networks

Nature Physics volume 21, pages 353–361 (2025)Cite this article

Subjects

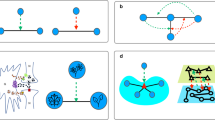
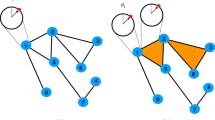
Abstract

Higher-order networks capture the many-body interactions present in complex systems, shedding light on the interplay between topology and dynamics. The theory of higher-order topological dynamics, which combines higher-order interactions with discrete topology and nonlinear dynamics, has the potential to enhance our understanding of complex systems, such as the brain and the climate, and to advance the development of next-generation AI algorithms. This theoretical framework, which goes beyond traditional node-centric descriptions, encodes the dynamics of a network through topological signals—variables assigned not only to nodes but also to edges, triangles and other higher-order cells. Recent findings show that topological signals lead to the emergence of distinct types of dynamical state and collective phenomena, including topological and Dirac synchronization, pattern formation and triadic percolation. These results offer insights into how topology shapes dynamics, how dynamics learns topology and how topology evolves dynamically. This Perspective primarily aims to guide physicists, mathematicians, computer scientists and network scientists through the emerging field of higher-order topological dynamics, while also outlining future research challenges.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: The emerging field of higher-order topological dynamics of complex systems.
Fig. 2: The dynamical state of a higher-order network.
Fig. 3: The topological Kuramoto model and global synchronization.
Fig. 4: The properties of the topological Dirac operator and the topological Dirac equation.
Fig. 5: Signed triadic interactions and the phase diagram of triadic percolation.

Similar content being viewed by others

References

  1. Barabási, A. L. Network Science (Cambridge Univ. Press, 2016).

  2. Newman, M. Networks (Oxford Univ. Press, 2018).

  3. Barrat, A., Barthelemy, M. & Vespignani, A. Dynamical Processes on Complex Networks (Cambridge Univ. Press, 2008).

  4. Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. Critical phenomena in complex networks. Rev. Mod. Phys. 80, 1275 (2008).

    ADS  Google Scholar 

  5. Masuda, N. & Lambiotte, R. A Guide to Temporal Networks (World Scientific, 2016).

  6. Bianconi, G. Multilayer Networks: Structure and Function (Oxford Univ. Press, 2018).

  7. Giusti, C., Ghrist, R. & Bassett, D. S. Two’s company, three (or more) is a simplex: algebraic-topological tools for understanding higher-order structure in neural data. J. Comput. Neurosci. 41, 1–14 (2016).

    MathSciNet  Google Scholar 

  8. Giusti, C., Pastalkova, E., Curto, C. & Itskov, V. Clique topology reveals intrinsic geometric structure in neural correlations. Proc. Natl Acad. Sci. USA 112, 13455–13460 (2015).

    ADS  MathSciNet  Google Scholar 

  9. Petri, G. et al. Homological scaffolds of brain functional networks. J. R. Soc. Interface 11, 20140873 (2014).

    Google Scholar 

  10. Faskowitz, J., Betzel, R. F. & Sporns, O. Edges in brain networks: contributions to models of structure and function. Netw. Neurosci. 6, 1–28 (2022).

    Google Scholar 

  11. Santoro, A., Battiston, F., Petri, G. & Amico, E. Higher-order organization of multivariate time series. Nat. Phys. 19, 221–229 (2023).

    Google Scholar 

  12. Reimann, M. W. et al. Cliques of neurons bound into cavities provide a missing link between structure and function. Front. Comput. Neurosci. 11, 48 (2017).

    Google Scholar 

  13. Iacopini, I., Petri, G., Barrat, A. & Latora, V. Simplicial models of social contagion. Nat. Commun. 10, 2485 (2019).

    ADS  Google Scholar 

  14. St-Onge, G., Sun, H., Allard, A., Hébert-Dufresne, L. & Bianconi, G. Universal nonlinear infection kernel from heterogeneous exposure on higher-order networks. Phys. Rev. Lett. 127, 158301 (2021).

    ADS  MathSciNet  Google Scholar 

  15. Ferraz de Arruda, G., Tizzani, M. & Moreno, Y. Phase transitions and stability of dynamical processes on hypergraphs. Commun. Phys. 4, 24 (2021).

    Google Scholar 

  16. Landry, N. W. & Restrepo, J. G. The effect of heterogeneity on hypergraph contagion models. Chaos 30, 103117 (2020).

    ADS  MathSciNet  Google Scholar 

  17. Grilli, J., Barabás, G., Michalska-Smith, M. J. & Allesina, S. Higher-order interactions stabilize dynamics in competitive network models. Nature 548, 210–213 (2017).

    ADS  Google Scholar 

  18. Tumminello, M., Aste, T., Di Matteo, T. & Mantegna, R. N. A tool for filtering information in complex systems. Proc. Natl Acad. Sci. USA 102, 10421–10426 (2005).

    ADS  Google Scholar 

  19. Massara, G. P., Di Matteo, T. & Aste, T. Network filtering for big data: triangulated maximally filtered graph. J. Complex Netw. 5, 161–178 (2016).

    MathSciNet  Google Scholar 

  20. Bianconi, G. Higher-Order Networks: An Introduction to Simplicial Complexes (Cambridge Univ. Press, 2021).

  21. Bick, C., Gross, E., Harrington, H. A. & Schaub, M. T. What are higher-order networks? SIAM Rev. 65, 686–731 (2023).

    MathSciNet  Google Scholar 

  22. Battiston, F. et al. The physics of higher-order interactions in complex systems. Nat. Phys. 17, 1093–1098 (2021).

    Google Scholar 

  23. Battiston, F. et al. Networks beyond pairwise interactions: structure and dynamics. Phys. Rep. 874, 1–92 (2020).

    ADS  MathSciNet  Google Scholar 

  24. Torres, L., Blevins, A. S., Bassett, D. & Eliassi-Rad, T. The why, how, and when of representations for complex systems. SIAM Rev. 63, 435–485 (2021).

    MathSciNet  Google Scholar 

  25. Majhi, S., Perc, M. & Ghosh, D. Dynamics on higher-order networks: a review. J. R. Soc. Interf. 19, 20220043 (2022).

    Google Scholar 

  26. Salnikov, V., Cassese, D. & Lambiotte, R. Simplicial complexes and complex systems. Euro. J. Phys. 40, 014001 (2018).

    Google Scholar 

  27. Boccaletti, S. et al. The structure and dynamics of networks with higher order interactions. Phys. Rep. 1018, 1–64 (2023).

    ADS  MathSciNet  Google Scholar 

  28. Hensel, F., Moor, M. & Rieck, B. A survey of topological machine learning methods. Front. Artif. Intell. 4, 681108 (2021).

    Google Scholar 

  29. Otter, N., Porter, M. A., Tillmann, U., Grindrod, P. & Harrington, H. A. A roadmap for the computation of persistent homology. EPJ Data Sci. 6, 1–38 (2017).

    Google Scholar 

  30. Vaccarino, F., Fugacci, U. & Scaramuccia, S. in Higher-Order Systems (eds Battiston, F. & Petri, G.) 97–139 (Springer, 2022).

  31. Petri, G., Scolamiero, M., Donato, I. & Vaccarino, F. Topological strata of weighted complex networks. PloS ONE 8, e66506 (2013).

    ADS  Google Scholar 

  32. Patania, A., Petri, G. & Vaccarino, F. The shape of collaborations. EPJ Data Sci. 6, 1–16 (2017).

    Google Scholar 

  33. Bianconi, G. & Ziff, R. M. Topological percolation on hyperbolic simplicial complexes. Phys. Rev. E 98, 052308 (2018).

    ADS  Google Scholar 

  34. Santos, F. A. et al. Topological phase transitions in functional brain networks. Phys. Rev. E 100, 032414 (2019).

    ADS  MathSciNet  Google Scholar 

  35. Lee, Y., Lee, J., Oh, S. M., Lee, D. & Kahng, B. Homological percolation transitions in growing simplicial complexes. Chaos 31, 041102 (2021).

    ADS  MathSciNet  Google Scholar 

  36. Baccini, F., Geraci, F. & Bianconi, G. Weighted simplicial complexes and their representation power of higher-order network data and topology. Phys. Rev. E 106, 034319 (2022).

    ADS  MathSciNet  Google Scholar 

  37. Muhammad, A. & Egerstedt, M. Control using higher order Laplacians in network topologies. In Proc. 17th International Symposium on Mathematical Theory of Networks and Systems 1024–1038 (Citeseer, 2006).

  38. Torres, J. J. & Bianconi, G. Simplicial complexes: higher-order spectral dimension and dynamics. Journal of Physics: Complexity 1, 015002 (2020).

    ADS  Google Scholar 

  39. Taylor, D. et al. Topological data analysis of contagion maps for examining spreading processes on networks. Nat. Commun. 6, 7723 (2015).

    ADS  Google Scholar 

  40. Schaub, M. T., Benson, A. R., Horn, P., Lippner, G. & Jadbabaie, A. Random walks on simplicial complexes and the normalized Hodge 1-Laplacian. SIAM Review 62, 353–391 (2020).

    MathSciNet  Google Scholar 

  41. Millán, A. P., Torres, J. J. & Bianconi, G. Explosive higher-order Kuramoto dynamics on simplicial complexes. Phys. Rev. Lett. 124, 218301 (2020).

    ADS  MathSciNet  Google Scholar 

  42. Carletti, T., Giambagli, L. & Bianconi, G. Global topological synchronization on simplicial and cell complexes. Phys. Rev. Lett. 130, 187401 (2023).

    ADS  MathSciNet  Google Scholar 

  43. Calmon, L., Restrepo, J. G., Torres, J. J. & Bianconi, G. Dirac synchronization is rhythmic and explosive. Commun. Phys. 5, 253 (2022).

    Google Scholar 

  44. Arnaudon, A., Peach, R. L., Petri, G. & Expert, P. Connecting Hodge and Sakaguchi-Kuramoto through a mathematical framework for coupled oscillators on simplicial complexes. Commun. Phys. 5, 211 (2022).

    Google Scholar 

  45. DeVille, L. Consensus on simplicial complexes: results on stability and synchronization. Chaos 31, 023137 (2021).

    ADS  MathSciNet  Google Scholar 

  46. Calmon, L., Krishnagopal, S. & Bianconi, G. Local Dirac synchronization on networks. Chaos 33, 033117 (2023).

    ADS  MathSciNet  Google Scholar 

  47. Carletti, T., Giambagli, L., Muolo, R. & Bianconi, G. Global topological Dirac synchronization. Preprint at https://arxiv.org/abs/2410.15338 (2024).

  48. Giambagli, L., Calmon, L., Muolo, R., Carletti, T. & Bianconi, G. Diffusion-driven instability of topological signals coupled by the Dirac operator. Phys. Rev. E 106, 064314 (2022).

    ADS  MathSciNet  Google Scholar 

  49. Muolo, R., Carletti, T. & Bianconi, G. The three way Dirac operator and dynamical Turing and Dirac induced patterns on nodes and links. Chaos Soliton. Fract. 178, 114312 (2024).

    MathSciNet  Google Scholar 

  50. Sun, H., Radicchi, F., Kurths, J. & Bianconi, G. The dynamic nature of percolation on networks with triadic interactions. Nat. Commun. 14, 1308 (2023).

    ADS  Google Scholar 

  51. Millán, A. P., Sun, H., Torres, J. J. & Bianconi, G. Triadic percolation induces dynamical topological patterns in higher-order networks. PNAS Nexus 3, pgae270 (2024).

  52. Sun, H. & Bianconi, G. Higher-order triadic percolation on random hypergraphs. Phys. Rev. E 110, 064315 (2024).

    MathSciNet  Google Scholar 

  53. Herron, L., Sartori, P. & Xue, B. Robust retrieval of dynamic sequences through interaction modulation. PRX Life 1, 023012 (2023).

    Google Scholar 

  54. Kozachkov, L., Slotine, J.-J. & Krotov, D. Neuron-astrocyte associative memory. Preprint at https://arxiv.org/abs/2311.08135 (2023).

  55. Barbarossa, S. & Sardellitti, S. Topological signal processing over simplicial complexes. IEEE Trans. Signal Process. 68, 2992–3007 (2020).

    ADS  MathSciNet  Google Scholar 

  56. Calmon, L., Schaub, M. T. & Bianconi, G. Dirac signal processing of higher-order topological signals. New J. Phys. 25, 093013 (2023).

    ADS  MathSciNet  Google Scholar 

  57. Roddenberry, T. M., Glaze, N. & Segarra, S. Principled simplicial neural networks for trajectory prediction. In International Conference on Machine Learning 9020–9029 (PMLR, 2021).

  58. Schaub, M. T., Zhu, Y., Seby, J.-B., Roddenberry, T. M. & Segarra, S. Signal processing on higher-order networks: livin’ on the edge… and beyond. Signal Process. 187, 108149 (2021).

    Google Scholar 

  59. Papamarkou, T. et al. Position paper: challenges and opportunities in topological deep learning. Preprint at https://arxiv.org/abs/2402.08871 (2024).

  60. Millán, A. P. et al. Repository for Topology Shapes Dynamics. GitHub https://github.com/Jamba15/TopologyShapesDynamics (2024).

  61. Katifori, E., Szöllősi, G. J. & Magnasco, M. O. Damage and fluctuations induce loops in optimal transport networks. Phys. Rev. Lett. 104, 048704 (2010).

    ADS  Google Scholar 

  62. Singh, M. et al. Fingerprint of volcanic forcing on the ENSO–Indian monsoon coupling. Sci. Adv. 6, eaba8164 (2020).

    ADS  Google Scholar 

  63. Kogut, J. B. An introduction to lattice gauge theory and spin systems. Rev. Mod. Phys. 51, 659 (1979).

    ADS  MathSciNet  Google Scholar 

  64. Banuls, M. C. et al. Simulating lattice gauge theories within quantum technologies. Eur. Phys. J. D 74, 1–42 (2020).

    Google Scholar 

  65. Bodnar, C. et al. Weisfeiler and Lehman go topological: message passing simplicial networks. In International Conference on Machine Learning 1026–1037 (PMLR, 2021).

  66. Grady, L. J. & Polimeni, J. R. Discrete Calculus: Applied Analysis on Graphs for Computational Science Vol. 3 (Springer, 2010).

  67. Ghorbanchian, R., Restrepo, J. G., Torres, J. J. & Bianconi, G. Higher-order simplicial synchronization of coupled topological signals. Comm. Phys. 4, 120 (2021).

    ADS  Google Scholar 

  68. Kuramoto, Y. Self-entrainment of a population of coupled non-linear oscillators. In International Symposium on Mathematical Problems in Theoretical Physics (ed. Araki, H.) 420–422 (Springer, 1975).

  69. Pikovsky, A., Rosenblum, M. & Kurths, J. Synchronization: a universal concept in nonlinear sciences. Self 2, 3 (2001).

    Google Scholar 

  70. Strogatz, S. From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. Phys. D 143, 1–20 (2000).

    MathSciNet  Google Scholar 

  71. Rodrigues, F. A., Peron, T. K. D., Ji, P. & Kurths, J. The Kuramoto model in complex networks. Phys. Rep. 610, 1–98 (2016).

    ADS  MathSciNet  Google Scholar 

  72. Fujisaka, H. & Yamada, T. Stability theory of synchronized motion in coupled-oscillator systems. Progr. Theor. Phys. 69, 32–47 (1983).

    ADS  MathSciNet  Google Scholar 

  73. Pecora, L. M. & Carroll, T. L. Master stability functions for synchronized coupled systems. Phys. Rev. Lett. 80, 2109 (1998).

    ADS  Google Scholar 

  74. Skardal, P. S. & Arenas, A. Memory selection and information switching in oscillator networks with higher-order interactions. J. Phys. Complex. 2, 015003 (2020).

    Google Scholar 

  75. Liu, Y.-Y. & Barabási, A.-L. Control principles of complex systems. Rev. Mod. Phys. 88, 035006 (2016).

    ADS  Google Scholar 

  76. Giusti, L., Battiloro, C., Di Lorenzo, P., Sardellitti, S. & Barbarossa, S. Simplicial attention neural networks. Preprint at https://arxiv.org/abs/2203.07485 (2022).

  77. Wang, R., Muolo, R., Carletti, T. & Bianconi, G. Global topological synchronization of weighted simplicial complexes. Phys. Rev. E 110, 014307 (2024).

    MathSciNet  Google Scholar 

  78. Eckmann, B. Harmonische funktionen und randwertaufgaben in einem komplex. Comment. Math. Helvetici 17, 240–255 (1944).

    MathSciNet  Google Scholar 

  79. Horak, D. & Jost, J. Spectra of combinatorial Laplace operators on simplicial complexes. Adv. Math. 244, 303–336 (2013).

    MathSciNet  Google Scholar 

  80. Reitz, M. & Bianconi, G. The higher-order spectrum of simplicial complexes: a renormalization group approach. J. Phys. A 53, 295001 (2020).

    MathSciNet  Google Scholar 

  81. Ziegler, C., Skardal, P. S., Dutta, H. & Taylor, D. Balanced Hodge Laplacians optimize consensus dynamics over simplicial complexes. Chaos 32, 023128 (2022).

    ADS  MathSciNet  Google Scholar 

  82. Krishnagopal, S. & Bianconi, G. Spectral detection of simplicial communities via Hodge Laplacians. Phys. Rev. E 104, 064303 (2021).

    ADS  MathSciNet  Google Scholar 

  83. Palla, G., Derényi, I., Farkas, I. & Vicsek, T. Uncovering the overlapping community structure of complex networks in nature and society. Nature 435, 814–818 (2005).

    ADS  Google Scholar 

  84. Becher, P. & Joos, H. The Dirac-Kähler equation and fermions on the lattice. Z. Phys. C 15, 343–365 (1982).

    ADS  MathSciNet  Google Scholar 

  85. Davies, E. Analysis on graphs and noncommutative geometry. J. Funct. Anal. 111, 398–430 (1993).

    MathSciNet  Google Scholar 

  86. Post, O. First order approach and index theorems for discrete and metric graphs. Ann. Henri Poincaré, 10, 823–866 (2009).

  87. Lloyd, S., Garnerone, S. & Zanardi, P. Quantum algorithms for topological and geometric analysis of data. Nat. Commun. 7, 10138 (2016).

    ADS  Google Scholar 

  88. Ameneyro, B., Siopsis, G. & Maroulas, V. Quantum persistent homology for time series. In 2022 IEEE/ACM 7th Symposium on Edge Computing 387–392 (IEEE, 2022).

  89. Bianconi, G. The topological Dirac equation of networks and simplicial complexes. J. Phys. Complex. 2, 035022 (2021).

    ADS  Google Scholar 

  90. Bianconi, G. The mass of simple and higher-order networks. J. Phys. A 57, 015001 (2023).

    ADS  MathSciNet  Google Scholar 

  91. Delporte, N., Sen, S. & Toriumi, R. Dirac walks on regular trees. J. Phys. A 57, 275002 (2023).

    MathSciNet  Google Scholar 

  92. Bianconi, G. Quantum entropy couples matter with geometry. J. Phys. A 57, 365002 (2024).

    MathSciNet  Google Scholar 

  93. Nurisso, M. et al. A unified framework for simplicial kuramoto models. Chaos 34, 053118 (2024).

    ADS  MathSciNet  Google Scholar 

  94. Eroglu, D. et al. See–saw relationship of the holocene east asian–australian summer monsoon. Nat. Commun. 7, 12929 (2016).

    ADS  Google Scholar 

  95. Turing, A. The chemical basis of morphogenesis. Phil. Trans. R. Soc. Lond. B 237, 37 (1952).

    ADS  MathSciNet  Google Scholar 

  96. Nakao, H. & Mikhailov, A. Turing patterns in network-organized activator-inhibitor systems. Nat. Phys. 6, 544 (2010).

    Google Scholar 

  97. Muolo, R., Giambagli, L., Nakao, H., Fanelli, D. & Carletti, T. Turing patterns on discrete topologies: from networks to higher-order structures. Proc. R. Soc. A 480, 20240235 (2024).

    MathSciNet  Google Scholar 

  98. Krishnagopal, S. & Bianconi, G. Topology and dynamics of higher-order multiplex networks. Chaos Soliton. Fract. 177, 114296 (2023).

    MathSciNet  Google Scholar 

  99. Wee, J., Bianconi, G. & Xia, K. Persistent Dirac for molecular representation. Sci. Rep. 13, 11183 (2023).

    ADS  Google Scholar 

  100. Suwayyid, F. & Wei, G.-W. Persistent Dirac of paths on digraphs and hypergraphs. Found. Data Sci. 6, 124–153 (2024).

    MathSciNet  Google Scholar 

  101. Hajij, M. et al. Combinatorial complexes: bridging the gap between cell complexes and hypergraphs. In 2023 57th Asilomar Conference on Signals, Systems, and Computers 799–803 (IEEE, 2023).

  102. Alain, M., Takao, S., Paige, B. & Deisenroth, M. P. Gaussian processes on cellular complexes. In International Conference on Machine Learning (2024).

  103. Battiloro, C. et al. Generalized simplicial attention neural networks. IEEE Trans. Signal Inf. Process. Netw. 10, 833–850 (2024).

    MathSciNet  Google Scholar 

  104. Nauck, C. et al. Deep graph predictions using Dirac-Bianconi graph neural networks. Open Rev. https://openreview.net/forum?id=AialDkY6y3 (2023).

  105. Nicoletti, G. & Busiello, D. M. Information propagation in multilayer systems with higher-order interactions across timescales. Phys. Rev. X 14, 021007 (2024).

    Google Scholar 

  106. Lee, S. H., Fricker, M. D. & Porter, M. A. Mesoscale analyses of fungal networks as an approach for quantifying phenotypic traits. J. Complex Netw. 5, 145–159 (2017).

    Google Scholar 

  107. Carletti, T., Battiston, F., Cencetti, G. & Fanelli, D. Random walks on hypergraphs. Phys. Rev. E 101, 022308 (2020).

    ADS  MathSciNet  Google Scholar 

  108. Neuhäuser, L., Lambiotte, R. & Schaub, M. T. Consensus dynamics on temporal hypergraphs. Phys. Rev. E 104, 064305 (2021).

    ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was partially supported by a grant from the Simons Foundation (to G.B.). A.P.M., H.S., T. C. and G.B. thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the programme Hypergraphs: Theory and Applications, where work on this paper was undertaken. This work was supported by EPSRC grant number EP/V521929/1. A.P.M. acknowledges financial support from the ‘Ramón y Cajal’ programme of the Spanish Ministry of Science and Innovation (grant number RYC2021-031241-I). A.P.M. and J.J.T. acknowledge financial support under grant number PID2023-149174NB-I00 financed by the Spanish Ministry and Agencia Estatal de Investigación MICIU/AEI/10.13039/501100011033 and EDRF funds (European Union). H.S. is supported by the Wallenberg Initiative on Networks and Quantum Information (WINQ). R.M. acknowledges JSPS, Japan KAKENHI JP22K11919, JP22H00516, and JST, Japan CREST JP-MJCR1913 for financial support. F.R. acknowledges support from the Army Research Office under contract number W911NF-21-1-0194 and the Air Force Office of Scientific Research under award numbers FA9550-21-1-0446 and FA9550-24-1-0039. G.B. acknowledges discussions with M. Niedostatek, R. Wang and A. A. A. Zaid.

Author information

Authors and Affiliations

  1. Institute ‘Carlos I’ for Theoretical and Computational Physics and Electromagnetism and Matter Physics Department, University of Granada, Granada, Spain

    Ana P. Millán & Joaquín J. Torres

  2. Nordita, KTH Royal Institute of Technology and Stockholm University, Stockholm, Sweden

    Hanlin Sun

  3. Department of Physics, Freie Universiät Berlin, Berlin, Germany

    Lorenzo Giambagli

  4. Department of Physics and Astronomy, University of Florence, INFN & CSDC, Sesto Fiorentino, Italy

    Lorenzo Giambagli

  5. Department of Systems and Control Engineering, Institute of Science Tokyo (former Tokyo Tech), Tokyo, Japan

    Riccardo Muolo

  6. Department of Mathematics and NaXys, Namur Institute for Complex Systems, University of Namur, Namur, Belgium

    Timoteo Carletti

  7. Center for Complex Networks and Systems Research, Luddy School of Informatics, Computing, and Engineering, Indiana University, Bloomington, IN, USA

    Filippo Radicchi

  8. Potsdam Institute for Climate Impact Research, Potsdam, Germany

    Jürgen Kurths

  9. Department of Physics, Humboldt University of Berlin, Berlin, Germany

    Jürgen Kurths

  10. School of Mathematical Sciences, Queen Mary University of London, London, UK

    Ginestra Bianconi

  11. The Alan Turing Institute, The British Library, London, UK

    Ginestra Bianconi

Authors
  1. Ana P. Millán
    View author publications

    Search author on:PubMed Google Scholar

  2. Hanlin Sun
    View author publications

    Search author on:PubMed Google Scholar

  3. Lorenzo Giambagli
    View author publications

    Search author on:PubMed Google Scholar

  4. Riccardo Muolo
    View author publications

    Search author on:PubMed Google Scholar

  5. Timoteo Carletti
    View author publications

    Search author on:PubMed Google Scholar

  6. Joaquín J. Torres
    View author publications

    Search author on:PubMed Google Scholar

  7. Filippo Radicchi
    View author publications

    Search author on:PubMed Google Scholar

  8. Jürgen Kurths
    View author publications

    Search author on:PubMed Google Scholar

  9. Ginestra Bianconi
    View author publications

    Search author on:PubMed Google Scholar

Contributions

G.B. designed the project. A.P.M., H.S., L.G., R.M., T.C., J.J.T. and G.B. prepared the figures and wrote the codes. All authors wrote the manuscript.

Corresponding author

Correspondence to Ginestra Bianconi.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Millán, A.P., Sun, H., Giambagli, L. et al. Topology shapes dynamics of higher-order networks. Nat. Phys. 21, 353–361 (2025). https://doi.org/10.1038/s41567-024-02757-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-024-02757-w

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics