Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Entanglement accelerates quantum simulation

Nature Physics volume 21, pages 1338–1345 (2025)Cite this article

Subjects

Abstract

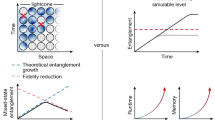
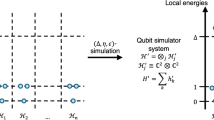
Quantum entanglement is an essential feature of many-body systems that impacts both quantum information processing and fundamental physics. Classical simulation methods can efficiently simulate many-body states with low entanglement, but struggle as the degree of entanglement grows. Here we investigate the relationship between quantum entanglement and quantum simulation, and show that product formula approximations for simulating many-body systems can perform better for entangled systems. We establish an upper bound for algorithmic error in terms of entanglement entropy that is tighter than previous results, and develop an adaptive simulation algorithm that incorporates measurement gadgets to estimate the algorithmic error. This shows that entanglement is not only an obstacle to classical simulation, but also a feature that can accelerate quantum algorithms.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Entanglement entropy and Trotter error in one segment.
Fig. 2: Comparison of theoretical bounds.
Fig. 3: Cost of different simulation methods and Trotter error terms in the light-cone structure.
Fig. 4: Number of Trotter steps determined with different error bounds for PF2.

Similar content being viewed by others

Code availability

The code used in this study is available via GitHub at https://github.com/zhaoqthu/Entanglement-accelerates-quantum-simulation.

References

  1. Amico, L., Fazio, R., Osterloh, A. & Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 80, 517–576 (2008).

    Article  MathSciNet  Google Scholar 

  2. Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009).

    Article  MathSciNet  Google Scholar 

  3. Walter, M., Gross, D. & Eisert, J. in Quantum Information: From Foundations to Quantum Technology Applications (eds Bruss, D. & Leuchs, G.) 293–330 (Wiley, 2016).

  4. Zeng, B., Chen, X., Zhou, D.-L. & Wen, X.-G. Quantum Information Meets Quantum Matter: From Quantum Entanglement to Topological Phases in Many-body Systems (Springer, 2019).

  5. Qi, X.-L. Does gravity come from quantum information? Nat. Phys. 14, 984–987 (2018).

    Article  Google Scholar 

  6. Vidal, G. Efficient classical simulation of slightly entangled quantum computations. Phys. Rev. Lett. 91, 147902 (2003).

    Article  Google Scholar 

  7. Datta, A., Shaji, A. & Caves, C. M. Quantum discord and the power of one qubit. Phys. Rev. Lett. 100, 050502 (2008).

    Article  Google Scholar 

  8. D’Alessio, L., Kafri, Y., Polkovnikov, A. & Rigol, M. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys. 65, 239–362 (2016).

    Article  Google Scholar 

  9. Gogolin, C. & Eisert, J. Equilibration, thermalisation, and the emergence of statistical mechanics in closed quantum systems. Rep. Progr. Phys. 79, 056001 (2016).

    Article  Google Scholar 

  10. Nandkishore, R. & Huse, D. A. Many-body localization and thermalization in quantum statistical mechanics. Annu. Rev. Condens. Matter Phys. 6, 15–38 (2015).

    Article  Google Scholar 

  11. Serbyn, M., Abanin, D. A. & Papić, Z. Quantum many-body scars and weak breaking of ergodicity. Nat. Phys. 17, 675–685 (2021).

    Article  Google Scholar 

  12. Cirac, J. I., Perez-Garcia, D., Schuch, N. & Verstraete, F. Matrix product states and projected entangled pair states: concepts, symmetries, theorems. Rev. Mod. Phys. 93, 045003 (2021).

    Article  MathSciNet  Google Scholar 

  13. Orús, R. Tensor networks for complex quantum systems. Nat. Rev. Phys. 1, 538–550 (2019).

    Article  Google Scholar 

  14. Altman, E. et al. Quantum simulators: architectures and opportunities. PRX Quantum 2, 017003 (2021).

    Article  Google Scholar 

  15. Lloyd, S. Universal quantum simulators. Science 273, 1073–1078 (1996).

    Article  MathSciNet  Google Scholar 

  16. Berry, D. W., Ahokas, G., Cleve, R. & Sanders, B. C. Efficient quantum algorithms for simulating sparse Hamiltonians. Commun. Math. Phys. 270, 359–371 (2007).

    Article  MathSciNet  Google Scholar 

  17. Berry, D. W. & Childs, A. M. Black-box Hamiltonian simulation and unitary implementation. Quantum Inf. Comput. 12, 29–62 (2012).

    MathSciNet  Google Scholar 

  18. Berry, D. W., Childs, A. M., Cleve, R., Kothari, R. & Somma, R. D. Simulating Hamiltonian dynamics with a truncated Taylor series. Phys. Rev. Lett. 114, 090502 (2015).

    Article  Google Scholar 

  19. Low, G. H. & Chuang, I. L. Optimal Hamiltonian simulation by quantum signal processing. Phys. Rev. Lett. 118, 010501 (2017).

    Article  MathSciNet  Google Scholar 

  20. Low, G. H. & Chuang, I. L. Hamiltonian simulation by qubitization. Quantum 3, 163 (2019).

    Article  Google Scholar 

  21. Childs, A. M. & Su, Y. Nearly optimal lattice simulation by product formulas. Phys. Rev. Lett. 123, 050503 (2019).

    Article  MathSciNet  Google Scholar 

  22. Childs, A. M., Maslov, D., Nam, Y., Ross, N. J. & Su, Y. Toward the first quantum simulation with quantum speedup. Proc. Natl Acad. Sci. USA 115, 9456–9461 (2018).

    Article  MathSciNet  Google Scholar 

  23. Childs, A. M., Su, Y., Tran, M. C., Wiebe, N. & Zhu, S. Theory of Trotter error with commutator scaling. Phys. Rev. X 11, 011020 (2021).

    Google Scholar 

  24. Şahinoğlu, B. & Somma, R. D. Hamiltonian simulation in the low-energy subspace. npj Quantum Inf. 7, 119 (2021).

    Article  Google Scholar 

  25. An, D., Fang, D. & Lin, L. Time-dependent unbounded Hamiltonian simulation with vector norm scaling. Quantum 5, 459 (2021).

    Article  Google Scholar 

  26. Zhao, Q., Zhou, Y., Shaw, A. F., Li, T. & Childs, A. M. Hamiltonian simulation with random inputs. Phys. Rev. Lett. 129, 270502 (2022).

    Article  MathSciNet  Google Scholar 

  27. Chen, C.-F. & Brandão, F. G. Average-case speedup for product formulas. Commun. Math. Phys. 405, 32 (2024).

    Article  MathSciNet  Google Scholar 

  28. Su, Y., Huang, H.-Y. & Campbell, E. T. Nearly tight Trotterization of interacting electrons. Quantum 5, 495 (2021).

    Article  Google Scholar 

  29. Scott, A. J. Multipartite entanglement, quantum-error-correcting codes, and entangling power of quantum evolutions. Phys. Rev. A 69, 052330 (2004).

    Article  Google Scholar 

  30. Hayden, P., Leung, D. W. & Winter, A. Aspects of generic entanglement. Commun. Math. Phys. 265, 95–117 (2006).

    Article  MathSciNet  Google Scholar 

  31. Suzuki, M. General theory of fractal path integrals with applications to many-body theories and statistical physics. J. Math. Phys. 32, 400–407 (1991).

    Article  MathSciNet  Google Scholar 

  32. Tran, M. C., Chu, S.-K., Su, Y., Childs, A. M. & Gorshkov, A. V. Destructive error interference in product-formula lattice simulation. Phys. Rev. Lett. 124, 220502 (2020).

    Article  MathSciNet  Google Scholar 

  33. Layden, D. First-order Trotter error from a second-order perspective. Phys. Rev. Lett. 128, 210501 (2022).

    Article  MathSciNet  Google Scholar 

  34. Kim, H., Ikeda, T. N. & Huse, D. A. Testing whether all eigenstates obey the eigenstate thermalization hypothesis. Phys. Rev. E 90, 052105 (2014).

    Article  Google Scholar 

  35. Shi, F., Li, M.-S., Chen, L. & Zhang, X. k-uniform quantum information masking. Phys. Rev. A 104, 032601 (2021).

    Article  MathSciNet  Google Scholar 

  36. Paeckel, S. et al. Time-evolution methods for matrix-product states. Ann. Phys. 411, 167998 (2019).

    Article  MathSciNet  Google Scholar 

  37. Bravyi, S., Hastings, M. B. & Verstraete, F. Lieb-Robinson bounds and the generation of correlations and topological quantum order. Phys. Rev. Lett. 97, 050401 (2006).

    Article  Google Scholar 

  38. Chen, B., Xu, J., Zhao, Q. & Yuan, X. Error interference in quantum simulation. Preprint at https://arxiv.org/abs/2411.03255 (2024).

  39. Aaronson, S. Shadow tomography of quantum states. SIAM J. Comput. 49, STOC18-368 (2019).

    Article  MathSciNet  Google Scholar 

  40. Huang, H.-Y., Kueng, R. & Preskill, J. Predicting many properties of a quantum system from very few measurements. Nat. Phys. 16, 1050–1057 (2020).

    Article  Google Scholar 

  41. Zhou, Y. & Liu, Q. Performance analysis of multi-shot shadow estimation. Quantum 7, 1044 (2023).

    Article  Google Scholar 

  42. Kovalsky, L. K. et al. Self-healing of Trotter error in digital adiabatic state preparation. Phys. Rev. Lett. 131, 060602 (2023).

    Article  Google Scholar 

  43. Yi, C. & Crosson, E. Spectral analysis of product formulas for quantum simulation. npj Quantum Inf 8, 37 (2022).

    Article  Google Scholar 

  44. Bravyi, S. Monte Carlo simulation of stoquastic Hamiltonians. Quantum Inf. Comput. 15, 1122–1140 (2015).

    MathSciNet  Google Scholar 

  45. Bravyi, S. & Gosset, D. Polynomial-time classical simulation of quantum ferromagnets. Phys. Rev. Lett. 119, 100503 (2017).

    Article  Google Scholar 

  46. Motta, M. et al. Determining eigenstates and thermal states on a quantum computer using quantum imaginary time evolution. Nat. Phys. 16, 205–210 (2020).

    Article  Google Scholar 

  47. Howard, M., Wallman, J., Veitch, V. & Emerson, J. Contextuality supplies the ‘magic’ for quantum computation. Nature 510, 351–355 (2014).

    Article  Google Scholar 

  48. Streltsov, A., Adesso, G. & Plenio, M. B. Colloquium: quantum coherence as a resource. Rev. Mod. Phys. 89, 041003 (2017).

    Article  MathSciNet  Google Scholar 

  49. Cotler, J. S. et al. Emergent quantum state designs from individual many-body wavefunctions. PRX Quantum 4, 010311 (2023).

    Article  Google Scholar 

  50. Huang, H.-Y., Kueng, R., Torlai, G., Albert, V. V. & Preskill, J. Provably efficient machine learning for quantum many-body problems. Science 377, eabk3333 (2022).

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

We thank W. Yu, F. Shi and J. Xu for helpful discussions. Q.Z. acknowledges funding from the Innovation Program for Quantum Science and Technology via Project No. 2024ZD0301900, the National Natural Science Foundation of China (NSFC) via Project Nos 12347104 and 12305030, the Guangdong Basic and Applied Basic Research Foundation via Project No. 2023A1515012185, the Hong Kong Research Grant Council (RGC) via Grant Nos 27300823, N_HKU718/23 and R6010-23, Guangdong Provincial Quantum Science Strategic Initiative No. GDZX2303007 and the HKU Seed Fund for Basic Research for New Staff via Project No. 2201100596. Y.Z. acknowledges the support of the Innovation Program for Quantum Science and Technology under Grant Nos 2024ZD0301900 and 2021ZD0302000, the NSFC under Grant No. 12205048, the Shanghai Science and Technology Innovation Action Plan under Grant No. 24LZ1400200, the Shanghai Municipal Science and Technology Grant No. 25TQ003 and start-up funding from Fudan University. A.M.C. acknowledges support from the United States Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Accelerated Research in Quantum Computing programme (Award No. DE-SC0020312) and from the National Science Foundation (QLCI Grant No. OMA-2120757).

Author information

Authors and Affiliations

  1. QICI Quantum Information and Computation Initiative, School of Computing and Data Science, The University of Hong Kong, Hong Kong, China

    Qi Zhao

  2. Key Laboratory for Information Science of Electromagnetic Waves (Ministry of Education), Fudan University, Shanghai, China

    You Zhou

  3. Hefei National Laboratory, Hefei, China

    You Zhou

  4. Department of Computer Science, Institute for Advanced Computer Studies, and Joint Center for Quantum Information and Computer Science, University of Maryland, College Park, MD, USA

    Andrew M. Childs

Authors
  1. Qi Zhao
    View author publications

    Search author on:PubMed Google Scholar

  2. You Zhou
    View author publications

    Search author on:PubMed Google Scholar

  3. Andrew M. Childs
    View author publications

    Search author on:PubMed Google Scholar

Contributions

Q.Z., Y.Z. and A.M.C. collaboratively initialized the research ideas, derived the mathematical proofs and wrote the manuscript. Q.Z. performed the numerical simulations.

Corresponding authors

Correspondence to Qi Zhao, You Zhou or Andrew M. Childs.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Burak Şahinoğlu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary information

Supplementary Sections I–VII and Figs. 1 and 2.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, Q., Zhou, Y. & Childs, A.M. Entanglement accelerates quantum simulation. Nat. Phys. 21, 1338–1345 (2025). https://doi.org/10.1038/s41567-025-02945-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-025-02945-2

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing