Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Frustrated electron hopping from the orbital configuration in a two-dimensional lattice

Nature Physics volume 21, pages 1260–1266 (2025)Cite this article

Subjects

Abstract

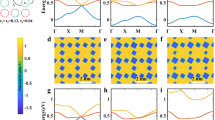
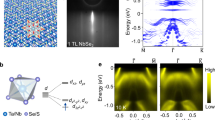
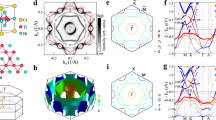
Electron hopping on spatially periodic lattices gives rise to intriguing electronic behaviour. For example, hopping on the geometrically frustrated two-dimensional kagome, dice and Lieb lattices yields electronic band structures with both massless Dirac-like and perfectly dispersion-less, flat bands. As materials featuring the dice and Lieb lattice structures are scarce, an alternative approach proposes to leverage atomic orbitals to realize the characteristic electron hopping of geometrically frustrated lattices. This strategy promises to expand the list of candidate materials with frustrated electron hopping, but is yet to be shown in experiments. Here we demonstrate frustrated hopping in the van der Waals intermetallic Pd5AlI2, emerging from the arrangement of atomic orbitals in a primitive square lattice. Using angle-resolved photoemission spectroscopy and quantum oscillation measurements, we reveal that the band structure of Pd5AlI2 includes linear Dirac-like bands intersected at their crossing point by a locally flat band—an essential characteristic of frustrated hopping in Lieb and dice lattices. Moreover, this compound shows exceptional chemical stability, with its unusual bulk band structure and metallicity persisting in ambient conditions down to the monolayer limit. Hence, our results showcase a way to realize electronic structures characteristic of geometrically frustrated lattices in non-frustrated systems.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Frustrated hopping from orbital decoration and the vdW metal Pd5AlI2.
Fig. 2: Bulk electronic structure and transport behaviour of Pd5AlI2.
Fig. 3: Electronic transport and fermiology towards the monolayer limit.
Fig. 4: Thickness-dependent Hall response and survey of vdW metals.

Similar content being viewed by others

Data availability

The data that support the findings of this study are presented in the published figures and tables and are available via the Harvard Dataverse repository at https://doi.org/10.7910/DVN/NAD0B9. Further data are available from the corresponding authors upon reasonable request.

References

  1. Stewart, G. R. Heavy-fermion systems. Rev. Mod. Phys. 56, 755–787 (1984).

    Article  ADS  Google Scholar 

  2. Bergman, D. L., Wu, C. & Balents, L. Band touching from real-space topology in frustrated hopping models. Phys. Rev. B 78, 125104 (2008).

    Article  ADS  Google Scholar 

  3. Mielke, A. Ferromagnetic ground states for the Hubbard model on line graphs. J. Phys. A: Math. Gen. 24, L73 (1991).

    Article  ADS  MathSciNet  Google Scholar 

  4. Horiguchi, T. & Chen, C. C. Lattice Green’s function for the diced lattice. J. Math. Phys. 15, 659–660 (1974).

    Article  ADS  Google Scholar 

  5. Lieb, E. H. Two theorems on the Hubbard model. Phys. Rev. Lett. 62, 1201–1204 (1989).

    Article  ADS  MathSciNet  Google Scholar 

  6. Yin, J.-X. et al. Quantum-limit Chern topological magnetism in TbMn6Sn6. Nature 583, 533–536 (2020).

    Article  ADS  Google Scholar 

  7. Kang, M. et al. Dirac fermions and flat bands in the ideal kagome metal FeSn. Nat. Mater. 19, 163–169 (2020).

    Article  ADS  Google Scholar 

  8. Ye, L. et al. Hopping frustration-induced flat band and strange metallicity in a kagome metal. Nat. Phys. 20, 610–614 (2024).

    Article  Google Scholar 

  9. Wakefield, J. P. et al. Three-dimensional flat bands in pyrochlore metal CaNi2. Nature 623, 301–306 (2023).

    Article  ADS  Google Scholar 

  10. Huang, J. et al. Non-Fermi liquid behaviour in a correlated flat-band pyrochlore lattice. Nat. Phys. 20, 603–609 (2024).

    Article  Google Scholar 

  11. Lee, C.-C., Fleurence, A., Yamada-Takamura, Y. & Ozaki, T. Hidden mechanism for embedding the flat bands of Lieb, kagome, and checkerboard lattices in other structures. Phys. Rev. B 100, 045150 (2019).

    Article  ADS  Google Scholar 

  12. Liu, H., Sethi, G., Meng, S. & Liu, F. Orbital design of flat bands in non-line-graph lattices via line-graph wave functions. Phys. Rev. B 105, 085128 (2022).

    Article  ADS  Google Scholar 

  13. Bercioux, D., Urban, D. F., Grabert, H. & Häusler, W. Massless Dirac-Weyl fermions in a 𝒯3 optical lattice. Phys. Rev. A 80, 063603 (2009).

    Article  ADS  Google Scholar 

  14. Xia, S. et al. Unconventional flatband line states in photonic Lieb lattices. Phys. Rev. Lett. 121, 263902 (2018).

    Article  ADS  Google Scholar 

  15. Shen, R., Shao, L. B., Wang, B. & Xing, D. Y. Single Dirac cone with a flat band touching on line-centered-square optical lattices. Phys. Rev. B 81, 041410 (2010).

    Article  ADS  Google Scholar 

  16. Santos, L. et al. Atomic quantum gases in kagomé lattices. Phys. Rev. Lett. 93, 030601 (2004).

    Article  ADS  Google Scholar 

  17. Jo, G.-B. et al. Ultracold atoms in a tunable optical kagome lattice. Phys. Rev. Lett. 108, 045305 (2012).

    Article  ADS  Google Scholar 

  18. Taie, S. et al. Coherent driving and freezing of bosonic matter wave in an optical Lieb lattice. Sci. Adv. 1, e1500854 (2015).

    Article  ADS  Google Scholar 

  19. Merker, H.-B., Schäfer, H. & Krebs, B. Neue PdxAly-phasen und die verbindung Pd5AII2. Z. Anorg. Allg. Chem. 462, 49–56 (1980).

    Article  Google Scholar 

  20. Le Blanc, M., Richter, K. & Schiebold, E. Eine früfung der tammannschen theorie der resistenzgrenzen am system gold–kupfer. Aufstellung neuer gesichtspunkte. Ann. Phys. 391, 929–1005 (1928).

    Article  Google Scholar 

  21. Lan, Z., Goldman, N., Bermudez, A., Lu, W. & Öhberg, P. Dirac-Weyl fermions with arbitrary spin in two-dimensional optical superlattices. Phys. Rev. B 84, 165115 (2011).

    Article  ADS  Google Scholar 

  22. Dóra, B., Kailasvuori, J. & Moessner, R. Lattice generalization of the Dirac equation to general spin and the role of the flat band. Phys. Rev. B 84, 195422 (2011).

    Article  ADS  Google Scholar 

  23. Semenoff, G. W. Condensed-matter simulation of a three-dimensional anomaly. Phys. Rev. Lett. 53, 2449–2452 (1984).

    Article  ADS  Google Scholar 

  24. Zhang, Y., Tan, Y.-W., Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 438, 201–204 (2005).

    Article  ADS  Google Scholar 

  25. Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005).

    Article  ADS  Google Scholar 

  26. Khestanova, E. et al. Unusual suppression of the superconducting energy gap and critical temperature in atomically thin NbSe2. Nano Lett. 18, 2623–2629 (2018).

    Article  ADS  Google Scholar 

  27. Park, C.-H., Yang, L., Son, Y.-W., Cohen, M. L. & Louie, S. G. Anisotropic behaviours of massless Dirac fermions in graphene under periodic potentials. Nat. Phys. 4, 213–217 (2008).

    Article  Google Scholar 

  28. Devarakonda, A. et al. Clean 2D superconductivity in a bulk van der Waals superlattice. Science 370, 231–236 (2020).

    Article  ADS  Google Scholar 

  29. Legros, A. et al. Universal T-linear resistivity and Planckian dissipation in overdoped cuprates. Nat. Phys. 15, 142–147 (2019).

    Article  Google Scholar 

  30. Cao, Y. et al. Strange metal in magic-angle graphene with near Planckian dissipation. Phys. Rev. Lett. 124, 076801 (2020).

    Article  ADS  Google Scholar 

  31. Ghiotto, A. et al. Quantum criticality in twisted transition metal dichalcogenides. Nature 597, 345–349 (2021).

    Article  ADS  Google Scholar 

  32. Hwang, E. H. & Das Sarma, S. Linear-in-T resistivity in dilute metals: a Fermi liquid perspective. Phys. Rev. B 99, 085105 (2019).

    Article  ADS  Google Scholar 

  33. Polshyn, H. et al. Large linear-in-temperature resistivity in twisted bilayer graphene. Nat. Phys. 15, 1011–1016 (2019).

    Article  Google Scholar 

  34. Cao, C. et al. Full control of solid-state electrolytes for electrostatic gating. Adv. Mater. 35, 2211993 (2023).

    Article  Google Scholar 

  35. Thinel, M. et al. Electronic bound states in the continuum in a 2D metal. Preprint at https://arxiv.org/abs/2410.19227 (2024).

  36. Urban, D. F., Bercioux, D., Wimmer, M. & Häusler, W. Barrier transmission of Dirac-like pseudospin-one particles. Phys. Rev. B 84, 115136 (2011).

    Article  ADS  Google Scholar 

  37. Weeks, C. & Franz, M. Topological insulators on the Lieb and perovskite lattices. Phys. Rev. B 82, 085310 (2010).

    Article  ADS  Google Scholar 

  38. Lai, H.-H., Grefe, S. E., Paschen, S. & Si, Q. Weyl–Kondo semimetal in heavy-fermion systems. Proc. Natl Acad. Sci. USA 115, 93–97 (2018).

    Article  ADS  Google Scholar 

  39. Ranninger, J. & Robaszkiewicz, S. Superconductivity of locally paired electrons. Phys. B+C 135, 468–472 (1985).

    Article  ADS  Google Scholar 

  40. Micnas, R., Ranninger, J. & Robaszkiewicz, S. Superconductivity in narrow-band systems with local nonretarded attractive interactions. Rev. Mod. Phys. 62, 113–171 (1990).

    Article  ADS  Google Scholar 

  41. Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).

    Article  ADS  Google Scholar 

  42. Treadwell, W. D. & Obrist, A. Über die bestimmung und bildung von oxydischen deckschichten auf aluminium. Helv. Chim. Acta 26, 1816–1828 (1943).

    Article  Google Scholar 

  43. Cabrera, N. & Mott, N. F. Theory of the oxidation of metals. Rep. Prog. Phys. 12, 163–184 (1949).

    Article  ADS  Google Scholar 

  44. Kepp, K. P. Chemical causes of metal nobleness. ChemPhysChem 21, 360–369 (2020).

    Article  Google Scholar 

  45. Bergman, G. Influence of spin-orbit coupling on weak localization. Phys. Rev. Lett. 48, 1046–1049 (1982).

    Article  ADS  Google Scholar 

  46. Das Sarma, S. & Stern, F. Single-particle relaxation time versus scattering time in an impure electron gas. Phys. Rev. B 32, 8442–8444 (1985).

    Article  ADS  Google Scholar 

  47. Rhodes, D., Chae, S. H., Ribeiro-Palau, R. & Hone, J. Disorder in van der Waals heterostructures of 2D materials. Nat. Mater. 18, 541–549 (2019).

    Article  ADS  Google Scholar 

  48. Zhu, J., Li, T., Young, A. F., Shan, J. & Mak, K. F. Quantum oscillations in two-dimensional insulators induced by graphite gates. Phys. Rev. Lett. 127, 247702 (2021).

    Article  ADS  Google Scholar 

  49. Briggs, N. et al. Atomically thin half-van der Waals metals enabled by confinement heteroepitaxy. Nat. Mater. 19, 637–643 (2020).

    Article  ADS  Google Scholar 

  50. Fang, N., Lee, H., Sun, C. & Zhang, X. Sub-diffraction-limited optical imaging with a silver superlens. Science 308, 534–537 (2005).

    Article  ADS  Google Scholar 

  51. da Jornada, F. H., Xian, L., Rubio, A. & Louie, S. G. Universal slow plasmons and giant field enhancement in atomically thin quasi-two-dimensional metals. Nat. Commun. 11, 1013 (2020).

    Article  ADS  Google Scholar 

  52. Rodrigo, D. et al. Mid-infrared plasmonic biosensing with graphene. Science 349, 165–168 (2015).

    Article  ADS  Google Scholar 

  53. Zagorac, D., Müller, H., Ruehl, S., Zagorac, J. & Rehme, S. Recent developments in the Inorganic Crystal Structure Database: theoretical crystal structure data and related features. J. Appl. Crystallogr. 52, 918–925 (2019).

    Article  ADS  Google Scholar 

  54. Sheldrick, G. M. SHELXT—integrated space-group and crystal-structure determination. Acta Cryst. A71, 3–8 (2015).

    Google Scholar 

  55. Sheldrick, G. M. Crystal structure refinement with SHELXL. Acta Cryst. C71, 3–8 (2015).

    Google Scholar 

  56. Dolomanov, O. V., Bourhis, L. J., Gildea, R. J., Howard, J. A. K. & Puschmann, H. OLEX2: a complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 42, 339–341 (2009).

    Article  ADS  Google Scholar 

  57. Giannozzi, P. et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 29, 465901 (2017).

    Article  Google Scholar 

  58. Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892–7895 (1990).

    Article  ADS  Google Scholar 

  59. Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).

    Article  ADS  Google Scholar 

  60. Georgescu, A. B., Millis, A. J. & Rondinelli, J. M. Trigonal symmetry breaking and its electronic effects in the two-dimensional dihalides MX2 and trihalides MX3. Phys. Rev. B 105, 245153 (2022).

    Article  ADS  Google Scholar 

  61. Georgescu, A. Wannier90 Hamiltonian tools. GitHub https://github.com/alexandrub53/Wannier90HamiltonianTools (2022).

  62. Kawamura, M. FermiSurfer: Fermi-surface viewer providing multiple representation schemes. Comput. Phys. Commun. 239, 197–203 (2019).

    Article  ADS  Google Scholar 

  63. Blaha, P. et al. WIEN2k: an APW+lo program for calculating the properties of solids. J. Chem. Phys. 152, 074101 (2020).

    Article  ADS  Google Scholar 

  64. Wasserman, S. R., Tao, Y. T. & Whitesides, G. M. Structure and reactivity of alkylsiloxane monolayers formed by reaction of alkyltrichlorosilanes on silicon substrates. Langmuir 5, 1074–1087 (1989).

    Article  Google Scholar 

  65. Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).

    Article  ADS  Google Scholar 

  66. Lee, H. N. S., McKinzie, H., Tannhauser, D. S. & Wold, A. The low‐temperature transport properties of NbSe2. J. Appl. Phys. 40, 602–604 (1969).

    Article  ADS  Google Scholar 

  67. Tsen, A. W. et al. Nature of the quantum metal in a two-dimensional crystalline superconductor. Nat. Phys. 12, 208–212 (2016).

    Article  Google Scholar 

  68. Zhao, S. Y. F. et al. Sign-reversing Hall effect in atomically thin high-temperature Bi2.1Sr1.9CaCu2.0O8+δ superconductors. Phys. Rev. Lett. 122, 247001 (2019).

    Article  ADS  Google Scholar 

  69. Zhu, C. S. et al. Evolution of transport properties in FeSe thin flakes with thickness approaching the two-dimensional limit. Phys. Rev. B 104, 024509 (2021).

    Article  ADS  Google Scholar 

  70. Lei, S. et al. High mobility in a van der Waals layered antiferromagnetic metal. Sci. Adv. 6, eaay6407 (2020).

  71. Lai, Z. et al. Metastable 1T′-phase group VIB transition metal dichalcogenide crystals. Nat. Mater. 20, 1113–1120 (2021).

    Article  ADS  Google Scholar 

  72. Lei, S. High mobility in a van der Waals layered antiferromagnetic metal. Sci. Adv. 6, eaay6407 (2020).

    Article  ADS  Google Scholar 

  73. Chen, L. et al. Exceptional electronic transport and quantum oscillations in thin bismuth crystals grown inside van der Waals materials. Nat. Mater. 23, 741–746 (2024).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank J. L. Pack, M. A. Kapfer, E. J. Telford, S. E. Turkel and J. G. Checkelsky for fruitful discussions. Research on novel hopping models was conducted as part of the Programmable Quantum Materials, an Energy Frontier Research Center, funded by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences, under award no. DE-SC0019443 (X.R., C.R.D., A.N.P., R.Q., X.Z. and M.D.). X.R. acknowledges support from a Brown Investigator Award, a program of the Brown Institute for Basic Sciences at the California Institute of Technology. The synthesis and structural characterization of the 2D metal were supported by the NSF MRSEC program through the Center for Precision-Assembled Quantum Materials at Columbia University, award no. DMR-2011738 (X.R., C.R.D., A.N.P. and X.Z.). X.Z. acknowledges support for STM/STS experiments by the Air Force Office of Scientific Research under award no. FA9550-22-1-0389. The Physical Property Measurement System used to perform vibrating-sample magnetometry and electrical transport measurements was purchased with financial support from the National Science Foundation through a supplement to award no. DMR-1751949 (X.R.). A.D. acknowledges support from the Simons Foundation Society of Fellows (grant no. 855186). High-magnetic-field measurements were performed at the National High Magnetic Field Laboratory, supported by the National Science Foundation Cooperative Agreement no. DMR-1644779 and the State of Florida. ARPES measurements used resources at the 21-ID (Electron Spectro-Microscopy) beamline of the National Synchrotron Light Source II, a US DOE, Office of Science User Facility, operated for the DOE, Office of Science, Brookhaven National Laboratory, under contract no. DE-SC0012704.

Author information

Author notes

  1. Aravind Devarakonda

    Present address: Department of Applied Physics and Applied Mathematics, Columbia University, New York, NY, USA

  2. Zhi Lin

    Present address: Department of Physics, Boston University, Boston, MA, USA

  3. These authors contributed equally: Aravind Devarakonda, Christie S. Koay, Daniel G. Chica.

Authors and Affiliations

  1. Department of Physics, Columbia University, New York, NY, USA

    Aravind Devarakonda, Sebastian Rossi, Madisen A. Holbrook, Abhay N. Pasupathy, Raquel Queiroz & Cory R. Dean

  2. Department of Chemistry, Columbia University, New York, NY, USA

    Christie S. Koay, Daniel G. Chica, Morgan Thinel, Sae Young Han, Michael E. Ziebel, Milan Delor, Xiaoyang Zhu & Xavier Roy

  3. Condensed Matter Physics and Materials Science Division, Brookhaven National Laboratory, Upton, NY, USA

    Asish K. Kundu & Abhay N. Pasupathy

  4. National Synchrotron Light Source II, Brookhaven National Laboratory, Upton, New York, NY, USA

    Asish K. Kundu, Anil Rajapitamahuni & Elio Vescovo

  5. Department of Applied Physics and Applied Mathematics, Columbia University, New York, NY, USA

    Zhi Lin

  6. Department of Chemistry, Indiana University, Bloomington, IN, USA

    Alexandru B. Georgescu

  7. Research Center for Electronic and Optical Materials, National Institute of Materials Science, Tsukuba, Japan

    Kenji Watanabe

  8. Research Center for Materials Nanoarchitectonics, National Institute of Materials Science, Tsukuba, Japan

    Takashi Taniguchi

Authors
  1. Aravind Devarakonda
    View author publications

    Search author on:PubMed Google Scholar

  2. Christie S. Koay
    View author publications

    Search author on:PubMed Google Scholar

  3. Daniel G. Chica
    View author publications

    Search author on:PubMed Google Scholar

  4. Morgan Thinel
    View author publications

    Search author on:PubMed Google Scholar

  5. Asish K. Kundu
    View author publications

    Search author on:PubMed Google Scholar

  6. Zhi Lin
    View author publications

    Search author on:PubMed Google Scholar

  7. Alexandru B. Georgescu
    View author publications

    Search author on:PubMed Google Scholar

  8. Sebastian Rossi
    View author publications

    Search author on:PubMed Google Scholar

  9. Sae Young Han
    View author publications

    Search author on:PubMed Google Scholar

  10. Michael E. Ziebel
    View author publications

    Search author on:PubMed Google Scholar

  11. Madisen A. Holbrook
    View author publications

    Search author on:PubMed Google Scholar

  12. Anil Rajapitamahuni
    View author publications

    Search author on:PubMed Google Scholar

  13. Elio Vescovo
    View author publications

    Search author on:PubMed Google Scholar

  14. Kenji Watanabe
    View author publications

    Search author on:PubMed Google Scholar

  15. Takashi Taniguchi
    View author publications

    Search author on:PubMed Google Scholar

  16. Milan Delor
    View author publications

    Search author on:PubMed Google Scholar

  17. Xiaoyang Zhu
    View author publications

    Search author on:PubMed Google Scholar

  18. Abhay N. Pasupathy
    View author publications

    Search author on:PubMed Google Scholar

  19. Raquel Queiroz
    View author publications

    Search author on:PubMed Google Scholar

  20. Cory R. Dean
    View author publications

    Search author on:PubMed Google Scholar

  21. Xavier Roy
    View author publications

    Search author on:PubMed Google Scholar

Contributions

C.S.K. and D.G.C. synthesized and characterized the bulk crystals. S.Y.H. supported with the energy-dispersive X-ray spectroscopy and scanning electron microscopy experiments, and M.E.Z. supported with the magnetization measurements. A.D. fabricated the nanodevices and performed the transport characterization. A.D., C.S.K. and D.G.C. conducted the high-field measurements. M.T. performed the STM characterization. A.K.K. performed the ARPES measurements with support from A.R. and E.V. K.W. and T.T. provided the hexagonal boron nitride crystals. Z.L., A.B.G., A.D. and R.Q. performed the theoretical calculations. A.N.P., R.Q., C.R.D. and X.R. supervised the project. A.D., C.R.D. and X.R. wrote the manuscript with input from all authors.

Corresponding authors

Correspondence to Aravind Devarakonda, Abhay N. Pasupathy, Raquel Queiroz, Cory R. Dean or Xavier Roy.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Zurab Guguchia, Hongyan Lu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 SEM imaging and EDS of Pd5AlI2.

a SEM image of Pd5AlI2 single crystal outlined in white. b EDS from a representative area scan on the crystal shown. Using statistics collected from ten area scans using the Al content as the reference, the Pd stoichiometry is 4.783 ± 0.174, Al stoichiometry is 1.0, and I stoichiometry is 1.843 ± 0.049.

Extended Data Fig. 2 ARPES electronic structure and photon energy dependence.

ARPES E(k) intensity map (LH polarization) along the \(\overline{\rm{M}}-\overline{{\Gamma}}-\overline{\rm{M}}\) line of the surface BZ at various incoming photon energies hν, a 127 eV b 136 eV and c 142 eV, probing distinct slices of kz, marked in e. The weak variation of these maps evidences the quasi-2D nature of the electronic structure. d ARPES Fermi surface cross-sections in the kx – ky plane (LV polarization) at various kz. The cross-sections are similarly invariant with kz. e An ARPES kz – k|| map along the \(\overline{\rm{M}}-\overline{{\Gamma}}-\overline{\rm{M}}\) line (LH polarization) exhibits cylindrical FSs for all three pockets. The dashed lines show the approximate kz sampled by the E(k) maps a – c. ARPES FS maps (hν = 125 eV) at f 100 meV g 150 meV h and 750 meV below EF. The experimental maps show good correspondence to DFT calculated FSs at i 100 meV j 150 meV and k 645 meV below EF.

Extended Data Fig. 3 Pd5AlI2 AFM topography and optical contrast.

a Topography of terraced Pd5AlI2 flake exfoliated onto SiO2/Si wafer measured by AFM with b linecut along magenta segment showing single Pd5AlI2 layer steps. c Optical microscope image of the same flake showing d contrast in the red, green, and blue color channels between regions of varying thickness. e Spinning a layer of PMMA over the flake f enhances optical contrast, making it easier to distinguish regions with different layer number.

Extended Data Table 1 Single crystal X-ray refinement
Full size table
Extended Data Table 2 Survey of exfoliated van der Waals metals
Full size table

Supplementary information

Supplementary Information

Supplementary Sections I–IV, Figs. 1–5 and Discussion.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Devarakonda, A., Koay, C.S., Chica, D.G. et al. Frustrated electron hopping from the orbital configuration in a two-dimensional lattice. Nat. Phys. 21, 1260–1266 (2025). https://doi.org/10.1038/s41567-025-02953-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-025-02953-2

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing