Constant-overhead magic state distillation

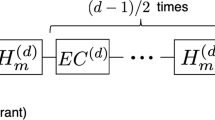
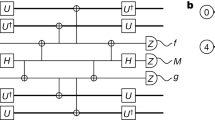
Abstract

Most schemes for realistic quantum computing require access to so-called magic states to allow universal quantum computing. Because the preparation process may be noisy, magic state distillation methods are needed to improve their accuracy and suppress any potential errors. Unfortunately, magic state distillation is resource-intensive and often considered a bottleneck to scalable quantum computation. Here, the cost is defined by the overhead: the ratio of noisy input magic states to cleaner outputs. This is known to scale as ${\mathcal{O}}({\log }^{\gamma }(1/\epsilon ))$ as ϵ → 0, where ϵ is the output error rate and γ is some constant. Reducing this overhead, corresponding to smaller γ, is highly desirable to remove the bottleneck. However, identifying the smallest achievable exponent γ for distilling magic states of qubits has proved challenging. Here, we resolve this problem by demonstrating protocols with the optimal exponent γ = 0, thus corresponding to magic state distillation with a constant overhead, and we show that this is achievable for the most important magic states such as $\left\vert {\mathsf{T}}\right\rangle$ and $\left\vert {\mathsf{CCZ}}\right\rangle$. This is achieved by using algebraic geometry constructions to build the first asymptotically good quantum codes with transversal non-Clifford gates, for which we also construct an efficient decoder with linear decoding radius.