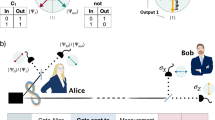
Abstract
The laws of quantum physics mean that prominent classical cryptographic protocols can be broken using quantum computers, but they also permit security guarantees that are classically impossible. For example, quantum states cannot be cloned, which restricts the capabilities of any adversary. Here we show that uncloneable encryption exists with no computational assumptions, with security approaching the ideal value as an inverse-polynomial function of the security parameter. With this scheme, two non-interacting adversaries cannot both learn an encrypted message, even if they are both given the encryption key. Our proof uses the properties of a monogamy-of-entanglement game associated with the Haar measure encryption. Using this connection, we show that any state that succeeds with high probability cannot be close to being maximally entangled between the referee and either of the adversaries. The decoupling principle then implies that either adversary becomes completely uncorrelated and, therefore, cannot win significantly better than random guessing.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to the full article PDF.
USD 39.95
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
Data availability
No datasets were generated during this study.
Code availability
No code was generated or used in the analysis and performance of this work.
References
Park, J. L. The concept of transition in quantum mechanics. Found. Phys. 1, 23–33 (1970).
Wootters, W. K. & Zurek, W. H. A single quantum cannot be cloned. Nature 299, 802–803 (1982).
Dieks, D. Communication by EPR devices. Phys. Lett. A 92, 271–272 (1982).
Bennett, C. H. & Brassard, G. Quantum cryptography: public key distribution and coin tossing. In Proc. International Conference on Computers, Systems and Signal Processing, 175–179 (1984).
Wiesner, S. Conjugate coding. ACM SIGACT News 15, 78–88 (1983).
Broadbent, A. & Lord, S. Uncloneable quantum encryption via oracles. In Proc. 15th Conference on the Theory of Quantum Computation, Communication and Cryptography—TQC 2020, 4–1422 (2020).
Ananth, P., Kaleoglu, F., Li, X., Liu, Q. & Zhandry, M. On the feasibility of unclonable encryption, and more. In Proc. Advances in Cryptology—CRYPTO 2022, 2, 212–241 (2022).
Ananth, P., Kaleoglu, F. & Liu, Q. Cloning games: a general framework for unclonable primitives. In Proc. Advances in Cryptology—CRYPTO 2023, 5, 66–98 (2023).
Chevalier, C., Hermouet, P. & Vu, Q.-H. Towards unclonable cryptography in the plain model. Preprint at http://arxiv.org/abs/2311.16663 (2024).
Ananth, P. & Behera, A. A modular approach to unclonable cryptography. In Proc. Advances in Cryptology—CRYPTO 2024, 7, 3–37 (2024).
Botteron, P. et al. Towards unconditional uncloneable encryption. Preprint at http://arxiv.org/abs/2410.23064 (2024).
Majenz, C., Schaffner, C. & Tahmasbi, M. Limitations on uncloneable encryption and simultaneous one-way-to-hiding. Preprint at https://arxiv.org/abs/2103.14510 (2021).
Tomamichel, M., Fehr, S., Kaniewski, J. & Wehner, S. A monogamy-of-entanglement game with applications to device-independent quantum cryptography. New J. Phys. 15, 103002 (2013).
Hiroka, T., Kitagawa, F., Nishimaki, R. & Yamakawa, T. Robust combiners and universal constructions for quantum cryptography. In Proc. Theory of Cryptography Conference, 126–158 (Springer, 2024).
Ananth, P. & Kaleoglu, F. Unclonable encryption, revisited. In Proc. 18th Theory of Cryptography Conference—TCC 2021, 1, 299–329 (2021).
Aaronson, S., Liu, J., Liu, Q., Zhandry, M. & Zhang, R. New approaches for quantum copy-protection. In Proc. Advances in Cryptology—CRYPTO 2021, 1, 526–555 (2021).
Coladangelo, A., Liu, J., Liu, Q. & Zhandry, M. Hidden cosets and applications to unclonable cryptography. In Proc. Advances in Cryptology—CRYPTO 2021, 1, 556–584 (2021).
Coladangelo, A., Majenz, C. & Poremba, A. Quantum copy-protection of compute-and-compare programs in the quantum random oracle model. Quantum 8, 1330 (2024).
Ananth, P. & La Placa, R. L. Secure software leasing. In Proc. Advances in Cryptology—EUROCRYPT 2021, 2, 501–530 (2021).
Broadbent, A., Jeffery, S., Lord, S., Podder, S. & Sundaram, A. Secure software leasing without assumptions. In Proc. 18th Theory of Cryptography Conference—TCC 2021, 1, 90–120 (2021).
Kitagawa, F., Nishimaki, R. & Yamakawa, T. Secure software leasing from standard assumptions. In Proc. 18th Theory of Cryptography Conference—TCC 2021, 31–61 (Springer, 2021).
Mehta, A. & Müller, A. Unclonable functional encryption. Preprint at http://arxiv.org/abs/2410.06029 (2024).
Georgiou, M. & Zhandry, M. Unclonable decryption keys. Preprint at Cryptology ePrint Archive http://eprint.iacr.org/2020/877 (2020).
Sattath, O. & Wyborski, S. Uncloneable decryptors from quantum copy-protection. Preprint at http://arxiv.org/abs/2203.05866 (2022).
Jawale, R. & Khurana, D. Unclonable non-interactive zero-knowledge. In Proc. International Conference on the Theory and Application of Cryptology and Information Security, 94–128 (Springer, 2025).
Bhattacharyya, A. & Culf, E. Uncloneable encryption from decoupling. Preprint at http://arxiv.org/pdf/2503.19125 (2025).
Poremba, A., Ragavan, S. & Vaikuntanathan, V. Cloning games, black holes and cryptography. Preprint at http://arxiv.org/abs/2411.04730 (2024).
Terhal, B. M. Is entanglement monogamous? IBM J. Res. Dev. 48, 71–78 (2004).
Culf, E. Quantum Uncloneability Games and Applications to Cryptography. Master’s thesis, Univ. Ottawa (2022).
Culf, E. & Vidick, T. A monogamy-of-entanglement game for subspace coset states. Quantum 6, 791 (2022).
Culf, E., Vidick, T. & Albert, V. V. Group coset monogamy games and an application to device-independent continuous-variable QKD. Preprint at http://arxiv.org/abs/2212.03935 (2022).
Johnston, N., Mittal, R., Russo, V. & Watrous, J. Extended non-local games and monogamy-of-entanglement games. Proc. R. Soc. Lond. Ser. A 472, 20160003 (2016).
Schumacher, B. & Westmoreland, M. D. Approximate quantum error correction. Quantum Inf. Process. 1, 5–12 (2002).
Dupuis, F. The Decoupling Approach to Quantum Information Theory. PhD thesis, Univ. Montréal (2010).
Hayden, P., Horodecki, M., Winter, A. & Yard, J. A decoupling approach to the quantum capacity. Open Syst. Inf. Dyn. 15, 7–19 (2008).
Majenz, C., Berta, M., Dupuis, F., Renner, R. & Christandl, M. Catalytic decoupling of quantum information. Phys. Rev. Lett. 118, 080503 (2017).
Alagic, G. & Majenz, C. Quantum non-malleability and authentication. In Proc. 14th Theory of Cryptography Conference—TCC 2017, 2, 310–341 (2017).
Lancien, C. & Majenz, C. Weak approximate unitary designs and applications to quantum encryption. Quantum 4, 313 (2020).
Dupuis, F., Berta, M., Wullschleger, J. & Renner, R. One-shot decoupling. Commun. Math. Phys. 328, 251–284 (2014).
Dankert, C., Cleve, R., Emerson, J. & Livine, E. Exact and approximate unitary 2-designs and their application to fidelity estimation. Phys. Rev. A 80, 012304 (2009).
Cleve, R., Leung, D., Liu, L. & Wang, C. Near-linear constructions of exact unitary 2-designs. Quantum Inf. Comput. 16, 721–756 (2016).
Acknowledgements
We are grateful to A. Broadbent for insightful discussions and helpful comments on a draft of the paper. A.B. thanks D. Leung for teaching her about decoupling. E.C. thanks everyone with whom he has discussed the uncloneable encryption problem in depth: P. Botteron, S. Kundu, S. Lord, A. Mehta, I. Nechita, M. Nevins, C. Pellegrini, D. Rochette, H. Salmasian and W. Slofstra. Research at the Perimeter Institute is supported in part by the Government of Canada through the Department of Innovation, Science, and Economic Development Canada and by the Province of Ontario through the Ministry of Colleges and Universities. E.C. is supported by a CGS D scholarship from NSERC.
Author information
Authors and Affiliations
Contributions
Both authors contributed equally to all aspects of this article and to the writing of the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Prabhanjan Ananth, Henry Yuen and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Technical preliminaries, technical lemmata and proofs of the main results.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Bhattacharyya, A., Culf, E. Uncloneable encryption from decoupling. Nat. Phys. 22, 315–318 (2026). https://doi.org/10.1038/s41567-025-03154-7
Received:
Accepted:
Published:
Version of record:
Issue date:
DOI: https://doi.org/10.1038/s41567-025-03154-7