Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Review
  • Published:

Training of physical neural networks

Nature volume 645, pages 53–61 (2025)Cite this article

Subjects

This article has been updated

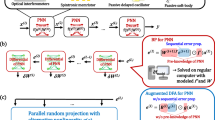
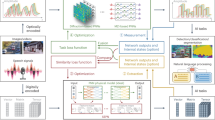
Abstract

Physical neural networks (PNNs) are a class of neural-like networks that make use of analogue physical systems to perform computations. Although at present confined to small-scale laboratory demonstrations, PNNs could one day transform how artificial intelligence (AI) calculations are performed. Could we train AI models many orders of magnitude larger than present ones? Could we perform model inference locally and privately on edge devices? Research over the past few years has shown that the answer to these questions is probably “yes, with enough research”. Because PNNs can make use of analogue physical computations more directly, flexibly and opportunistically than traditional computing hardware, they could change what is possible and practical for AI systems. To do this, however, will require notable progress, rethinking both how AI models work and how they are trained—primarily by considering the problems through the constraints of the underlying hardware physics. To train PNNs, backpropagation-based and backpropagation-free approaches are now being explored. These methods have various trade-offs and, so far, no method has been shown to scale to large models with the same performance as the backpropagation algorithm widely used in deep learning today. However, this challenge has been rapidly changing and a diverse ecosystem of training techniques provides clues for how PNNs may one day be used to create both more efficient and larger-scale realizations of present-scale AI models.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Physical neural networks.
Fig. 2: Training methods for PNNs.
Fig. 3: Analogue large models.

Similar content being viewed by others

Change history

  • 05 September 2025

    In the version of this article initially published, affiliation 8 listed outdated information and the affiliation is now updated in the HTML and PDF versions of the article.

References

  1. Samborska, V. Scaling up: how increasing inputs has made artificial intelligence more capable. Our World in Data https://ourworldindata.org/scaling-up-ai (2025).

  2. Sebastian, A., Le Gallo, M., Khaddam-Aljameh, R. & Eleftheriou, E. Memory devices and applications for in-memory computing. Nat. Nanotechnol. 15, 529–544 (2020).

    Article  ADS  CAS  PubMed  Google Scholar 

  3. Wetzstein, G. et al. Inference in artificial intelligence with deep optics and photonics. Nature 588, 39–47 (2020).

    Article  ADS  CAS  PubMed  Google Scholar 

  4. Wright, L. G. et al. Deep physical neural networks trained with backpropagation. Nature 601, 549–555 (2022).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  5. Tanaka, G. et al. Recent advances in physical reservoir computing: a review. Neural Netw. 115, 100–123 (2019).

    Article  PubMed  Google Scholar 

  6. Hughes, T. W., Williamson, I. A., Minkov, M. & Fan, S. Wave physics as an analog recurrent neural network. Sci. Adv. 5, eaay6946 (2019).

    Article  ADS  PubMed  PubMed Central  Google Scholar 

  7. Onodera, T. et al. Scaling on-chip photonic neural processors using arbitrarily programmable wave propagation. Preprint at https://arxiv.org/abs/2402.17750 (2024).

  8. Momeni, A., Rahmani, B., Malléjac, M., del Hougne, P. & Fleury, R. Backpropagation-free training of deep physical neural networks. Science 382, 1297–1303 (2023).

    Article  ADS  MathSciNet  CAS  PubMed  Google Scholar 

  9. Xu, Z. et al. Large-scale photonic chiplet Taichi empowers 160-TOPS/W artificial general intelligence. Science 384, 202–209 (2024).

    Article  ADS  CAS  PubMed  Google Scholar 

  10. Rumelhart, D. E., Hinton, G. E. & Williams, R. J. Learning representations by back-propagating errors. Nature 323, 533–536 (1986).

    Article  ADS  Google Scholar 

  11. Lin, X. et al. All-optical machine learning using diffractive deep neural networks. Science 361, 1004–1008 (2018).

    Article  ADS  MathSciNet  CAS  PubMed  Google Scholar 

  12. Le Gallo, M. et al. A 64-core mixed-signal in-memory compute chip based on phase-change memory for deep neural network inference. Nat. Electron. 6, 680–693 (2023).

    Article  Google Scholar 

  13. Chen, Z. et al. Deep learning with coherent VCSEL neural networks. Nat. Photon. 17, 723–730 (2023).

    Article  ADS  CAS  Google Scholar 

  14. Mengu, D. et al. Misalignment resilient diffractive optical networks. Nanophotonics 9, 4207–4219 (2020).

    Article  Google Scholar 

  15. Matsushima, K. & Shimobaba, T. Band-limited angular spectrum method for numerical simulation of free-space propagation in far and near fields. Opt. Express 17, 19662–19673 (2009).

    Article  ADS  CAS  PubMed  Google Scholar 

  16. Launay, J., Poli, I., Boniface, F. & Krzakala, F. Direct feedback alignment scales to modern deep learning tasks and architectures. Adv. Neural Inf. Process. Syst. 33, 9346–9360 (2020).

    Google Scholar 

  17. Cramer, B. et al. Surrogate gradients for analog neuromorphic computing. Proc. Natl Acad. Sci. 119, e2109194119 (2022).

    Article  MathSciNet  PubMed  PubMed Central  Google Scholar 

  18. Spall, J., Guo, X. & Lvovsky, A. I. Hybrid training of optical neural networks. Optica 9, 803–811 (2022).

    Article  ADS  Google Scholar 

  19. Lillicrap, T. P., Cownden, D., Tweed, D. B. & Akerman, C. J. Random synaptic feedback weights support error backpropagation for deep learning. Nat. Commun. 7, 13276 (2016).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  20. Brunton, S. L. & Kutz, J. N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control (Cambridge Univ. Press, 2022).

  21. Hinton, G. The forward-forward algorithm: some preliminary investigations. Preprint at https://arxiv.org/abs/2212.13345 (2022).

  22. Laydevant, J., Lott, A., Venturelli, D. & McMahon, P. L. The benefits of self-supervised learning for training physical neural networks. In Proc. 37th First Workshop on Machine Learning with New Compute Paradigms at NeurIPS 2023 (MLNPCP 2023) https://openreview.net/forum?id=Fik4cO7FXd (OpenReview, 2023).

  23. Refinetti, M., d’Ascoli, S., Ohana, R. & Goldt, S. Align, then memorise: the dynamics of learning with feedback alignment. In Proc. 38th International Conference on Machine Learning, 8925–8935 (MLR Press, 2021).

  24. Lillicrap, T. P., Cownden, D., Tweed, D. B. & Akerman, C. J. Random feedback weights support learning in deep neural networks. Preprint at https://arxiv.org/abs/1411.0247 (2014).

  25. Launay, J. et al. Hardware beyond backpropagation: a photonic co-processor for direct feedback alignment. Preprint at https://arxiv.org/abs/2012.06373 (2020).

  26. Nakajima, M. et al. Physical deep learning with biologically inspired training method: gradient-free approach for physical hardware. Nat. Commun. 13, 7847 (2022).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  27. Hinton, G. E., Dayan, P., Frey, B. J. & Neal, R. M. The “wake-sleep” algorithm for unsupervised neural networks. Science 268, 1158–1161 (1995).

    Article  ADS  CAS  PubMed  Google Scholar 

  28. Löwe, S., O’Connor, P. & Veeling, B. Putting an end to end-to-end: gradient-isolated learning of representations. In Proc. Advances in Neural Information Processing Systems 32 (NeuroIPS 2019), 3039–3051 (ACM, 2019).

  29. Nøkland, A. & Eidnes, L. H. Training neural networks with local error signals. In Proc. 36th International Conference on Machine Learning, 4839–4850 (MLR Press, 2019).

  30. Siddiqui, S. A., Krueger, D., LeCun, Y. & Deny, S. Blockwise self-supervised learning at scale. Preprint at https://arxiv.org/abs/2302.01647v1 (2023).

  31. Oguz, I. et al. Forward–forward training of an optical neural network. Opt. Lett. 48, 5249–5252 (2023).

    Article  ADS  PubMed  Google Scholar 

  32. Xue, Z. et al. Fully forward mode training for optical neural networks. Nature 632, 280–286 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  33. Spall, J. C. Multivariate stochastic approximation using a simultaneous perturbation gradient approximation. IEEE Trans. Autom. Control 37, 332–341 (1992).

    Article  MathSciNet  Google Scholar 

  34. McCaughan, A. N. et al. Multiplexed gradient descent: fast online training of modern datasets on hardware neural networks without backpropagation. APL Mach. Learn. 1, 026118 (2023).

    Article  Google Scholar 

  35. Bandyopadhyay, S. et al. Single-chip photonic deep neural network with forward-only training. Nat. Photon. 18, 1335–1343 (2024).

    Article  CAS  Google Scholar 

  36. Oguz, I. et al. Programming nonlinear propagation for efficient optical learning machines. Adv. Photonics 6, 016002 (2024).

    Article  ADS  CAS  Google Scholar 

  37. Skalli, A. et al. Annealing-inspired training of an optical neural network with ternary weights. Commun. Phys. 8, 68 (2025).

    Article  Google Scholar 

  38. Bueno, J. et al. Reinforcement learning in a large-scale photonic recurrent neural network. Optica 5, 756–760 (2018).

    Article  ADS  Google Scholar 

  39. Kanno, K., Naruse, M. & Uchida, A. Adaptive model selection in photonic reservoir computing by reinforcement learning. Sci. Rep. 10, 10062 (2020).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  40. Hermans, M., Burm, M., Van Vaerenbergh, T., Dambre, J. & Bienstman, P. Trainable hardware for dynamical computing using error backpropagation through physical media. Nat. Commun. 6, 6729 (2015).

    Article  ADS  CAS  PubMed  Google Scholar 

  41. Burr, G. W. et al. Neuromorphic computing using non-volatile memory. Adv. Phys. X 2, 034092 (2017).

    Google Scholar 

  42. Pai, S. et al. Experimentally realized in situ backpropagation for deep learning in photonic neural networks. Science 380, 398–404 (2023).

    Article  ADS  CAS  PubMed  Google Scholar 

  43. Morichetti, F. et al. Non-invasive on-chip light observation by contactless waveguide conductivity monitoring. IEEE J. Sel. Top. Quantum Electron. 20, 292–301 (2014).

    Article  ADS  Google Scholar 

  44. Zhou, T. et al. In situ optical backpropagation training of diffractive optical neural networks. Photonics Res. 8, 940–953 (2020).

    Article  CAS  Google Scholar 

  45. Guo, X., Barrett, T. D., Wang, Z. M. & Lvovsky, A. Backpropagation through nonlinear units for the all-optical training of neural networks. Photonics Res. 9, B71–B80 (2021).

    Article  Google Scholar 

  46. Wanjura, C. C. & Marquardt, F. Fully nonlinear neuromorphic computing with linear wave scattering. Nat. Phys. 20, 1434–1440 (2024).

    Article  CAS  Google Scholar 

  47. Yildirim, M., Dinc, N. U., Oguz, I., Psaltis, D. & Moser, C. Nonlinear processing with linear optics. Nat. Photon. 18, 1076–1082 (2024).

    Article  CAS  Google Scholar 

  48. Xia, F. et al. Nonlinear optical encoding enabled by recurrent linear scattering. Nat. Photon. 18, 1067–1075 (2024).

  49. Scellier, B. & Bengio, Y. Equilibrium propagation: bridging the gap between energy-based models and backpropagation. Front. Comput. Neurosci. 11, 24 (2017).

    Article  PubMed  PubMed Central  Google Scholar 

  50. Ackley, D. H., Hinton, G. E. & Sejnowski, T. J. A learning algorithm for Boltzmann machines. Cogn. Sci. 9, 147–169 (1985).

    Google Scholar 

  51. Stern, M., Hexner, D., Rocks, J. W. & Liu, A. J. Supervised learning in physical networks: from machine learning to learning machines. Phys. Rev. X 11, 021045 (2021).

    CAS  Google Scholar 

  52. Scellier, B., Ernoult, M., Kendall, J. & Kumar, S. Energy-based learning algorithms for analog computing: a comparative study. In Proc. 37th International Conference on Neural Information Processing Systems (NIPS ’23), 52705–52731 (ACM, 2023).

  53. Kendall, J., Pantone, R., Manickavasagam, K., Bengio, Y. & Scellier, B. Training end-to-end analog neural networks with equilibrium propagation. Preprint at https://arxiv.org/abs/2006.01981 (2020).

  54. Wang, Q., Wanjura, C. C. & Marquardt, F. Training coupled phase oscillators as a neuromorphic platform using equilibrium propagation. Neuromorph. Comput. Eng. 4, 034014 (2024).

    Article  Google Scholar 

  55. Yi, S.-i, Kendall, J. D., Williams, R. S. & Kumar, S. Activity-difference training of deep neural networks using memristor crossbars. Nat. Electron. 6, 45–51 (2023).

    Google Scholar 

  56. Laydevant, J., Marković, D. & Grollier, J. Training an Ising machine with equilibrium propagation. Nat. Commun. 15, 3671 (2024).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  57. Altman, L. E., Stern, M., Liu, A. J. & Durian, D. J. Experimental demonstration of coupled learning in elastic networks. Phys. Rev. Appl. 22, 024053 (2024).

    Article  CAS  Google Scholar 

  58. Dillavou, S., Stern, M., Liu, A. J. & Durian, D. J. Demonstration of decentralized physics-driven learning. Phys. Rev. Appl. 18, 014040 (2022).

    Article  ADS  CAS  Google Scholar 

  59. Dillavou, S. et al. Machine learning without a processor: emergent learning in a nonlinear analog network. Proc. Natl Acad. Sci. 121, e2319718121 (2024).

  60. Stern, M., Dillavou, S., Jayaraman, D., Duria, D. J. & Liu, A. J. Training self-learning circuits for power-efficient solutions. APL Mach. Learn. 2, 016114 (2024).

    Article  Google Scholar 

  61. Anisetti, V. R., Kandala, A., Scellier, B. & Schwarz, J. Frequency propagation: multimechanism learning in nonlinear physical networks. Neural Comput. 36, 596–620 (2024).

    Article  MathSciNet  PubMed  Google Scholar 

  62. Murugan, A., Strupp, A., Scellier, B. & Falk, M. Contrastive learning through non-equilibrium memory. In APS March Meeting Abstracts 2023, F02.005 (APS, 2023).

  63. Laborieux, A. & Zenke, F. Holomorphic equilibrium propagation computes exact gradients through finite size oscillations. In Proc. 36th International Conference on Neural Information Processing Systems (NIPS ’22), 12950–12963 (ACM, 2022).

  64. Scellier, B., Mishra, S., Bengio, Y. & Ollivier, Y. Agnostic physics-driven deep learning. Preprint at https://arxiv.org/abs/2205.15021 (2022).

  65. Lopez-Pastor, V. & Marquardt, F. Self-learning machines based on Hamiltonian echo backpropagation. Phys. Rev. X 13, 031020 (2023).

    CAS  Google Scholar 

  66. Touvron, H. et al. LLaMA: open and efficient foundation language models. Preprint at https://arxiv.org/abs/2302.13971 (2023).

  67. Chowdhery, A. et al. PaLM: scaling language modeling with pathways. J. Mach. Learn. Res. 24, 1–113 (2023).

    Google Scholar 

  68. Achiam, J. et al. GPT-4 technical report. Preprint at https://arxiv.org/abs/2303.08774v1 (2023).

  69. Team, G. Gemini: a family of highly capable multimodal models. Preprint at https://arxiv.org/abs/2312.11805v1 (2024).

  70. Radford, A. et al. Learning transferable visual models from natural language supervision. In Proc. 38th International Conference on Machine Learning, 8748–8763 (MLR Press, 2021).

  71. Liu, H., Li, C., Wu, Q. & Lee, Y. J. Visual instruction tuning. In Proc. 37th Conference on Neural Information Processing Systems (NeurIPS 2023) https://openreview.net/forum?id=w0H2xGHlkw (OpenReview, 2023).

  72. Radford, A. et al. Language models are unsupervised multitask learners. OpenAI Blog 1, 9 (2019).

    Google Scholar 

  73. Katharopoulos, A., Vyas, A., Pappas, N. & Fleuret, F. Transformers are RNNs: fast autoregressive transformers with linear attention. In Proc. 37th International Conference on Machine Learning, 5156–5165 (MLR Press, 2020).

  74. Gu, A. & Dao, T. Mamba: linear-time sequence modeling with selective state spaces. Preprint at https://arxiv.org/abs/2312.00752v1 (2023).

  75. Wang, H. et al. BitNet: scaling 1-bit transformers for large language models. Preprint at https://arxiv.org/abs/2310.11453 (2023).

  76. Hu, E. J. et al. LoRA: low-rank adaptation of large language models. Preprint at https://arxiv.org/abs/2106.09685 (2021).

  77. Dao, T., Fu, D., Ermon, S., Rudra, A. & Ré, C. FLASHATTENTION: fast and memory-efficient exact attention with IO-awareness. In Proc. 36th Conference on Neural Information Processing Systems (NeurIPS 2022) 35, 16344–16359 (ACM, 2022).

  78. Juravsky, J. et al. Hydragen: high-throughput LLM inference with shared prefixes. Preprint at https://arxiv.org/abs/2402.05099 (2024).

  79. Anderson, M. G., Ma, S.-Y., Wang, T., Wright, L. G. & McMahon, P. L. Optical transformers. Preprint at https://arxiv.org/abs/2302.10360 (2023).

  80. Shen, Y. et al. Deep learning with coherent nanophotonic circuits. Nat. Photon. 11, 441–446 (2017).

    Article  ADS  CAS  Google Scholar 

  81. Hamerly, R., Bernstein, L., Sludds, A., Soljačić, M. & Englund, D. Large-scale optical neural networks based on photoelectric multiplication. Phys. Rev. X 9, 021032 (2019).

    CAS  Google Scholar 

  82. Tait, A. N. Quantifying power in silicon photonic neural networks. Phys. Rev. Appl. 17, 054029 (2022).

    Article  ADS  Google Scholar 

  83. Laydevant, J., Wright, L. G., Wang, T. & McMahon, P. L. The hardware is the software. Neuron 112, 180–183 (2024).

    Article  CAS  PubMed  Google Scholar 

  84. Hooker, S. The hardware lottery. Commun. ACM 64, 58–65 (2021).

    Article  Google Scholar 

  85. Stroev, N. & Berloff, N. G. Analog photonics computing for information processing, inference, and optimization. Adv. Quantum Technol. 6, 2300055 (2023).

    Article  Google Scholar 

  86. Cerezo, M., Verdon, G., Huang, H.-Y., Cincio, L. & Coles, P. J. Challenges and opportunities in quantum machine learning. Nat. Comput. Sci. 2, 567–576 (2022).

    Article  CAS  PubMed  Google Scholar 

  87. Kashif, M. & Shafique, M. Hqnet: harnessing quantum noise for effective training of quantum neural networks in NISQ era. Preprint at https://arxiv.org/abs/2402.08475v1 (2024).

  88. Zhou, M.-G. et al. Quantum neural network for quantum neural computing. Research 6, 0134 (2023).

    Article  ADS  PubMed  PubMed Central  Google Scholar 

  89. Tian, J. et al. Recent advances for quantum neural networks in generative learning. IEEE Trans. Pattern. Anal. Mach. Intell. 45, 12321–12340 (2023).

    Article  PubMed  Google Scholar 

  90. Cerezo, M. et al. Variational quantum algorithms. Nat. Rev. Phys. 3, 625–644 (2021).

    Article  Google Scholar 

  91. Niazi, S. et al. Training deep Boltzmann networks with sparse Ising machines. Nat. Electron. 7, 610–619 (2024).

    Article  Google Scholar 

  92. Ma, S. Y., Wang, T., Laydevant, J., Wright, L. G. & McMahon, P. L. Quantum-limited stochastic optical neural networks operating at a few quanta per activation. Nat. Commun. 16, 359 (2025).

  93. Pierangeli, D., Marcucci, G., Brunner, D. & Conti, C. Noise-enhanced spatial-photonic Ising machine. Nanophotonics 9, 4109–4116 (2020).

    Article  Google Scholar 

  94. McMahon, P. L. The physics of optical computing. Nat. Rev. Phys. 5, 717–734 (2023).

    Article  Google Scholar 

  95. Keeling, J. & Berloff, N. G. Exciton–polariton condensation. Contemp. Phys. 52, 131–151 (2011).

    Article  ADS  CAS  Google Scholar 

  96. Berloff, N. G. et al. Realizing the classical XY Hamiltonian in polariton simulators. Nat. Mater. 16, 1120–1126 (2017).

    Article  ADS  CAS  PubMed  Google Scholar 

  97. Johnston, A. & Berloff, N. G. Macroscopic noise amplification by asymmetric dyads in non-Hermitian optical systems for generative diffusion models. Phys. Rev. Lett. 132, 096901 (2024).

    Article  ADS  MathSciNet  CAS  PubMed  Google Scholar 

  98. Wang, T. et al. Image sensing with multilayer nonlinear optical neural networks. Nat. Photon. 17, 408–415 (2023).

    Article  ADS  CAS  Google Scholar 

  99. Zhou, F. & Chai, Y. Near-sensor and in-sensor computing. Nat. Electron. 3, 664–671 (2020).

    Article  Google Scholar 

  100. del Hougne, P., F. Imani, M., Diebold, A. V., Horstmeyer, R. & Smith, D. R. Learned integrated sensing pipeline: reconfigurable metasurface transceivers as trainable physical layer in an artificial neural network. Adv. Sci. 7, 1901913 (2020).

    Article  Google Scholar 

  101. Vaswani, A. et al. Attention is all you need. In Proc. 31st International Conference on Neural Information Processing Systems (NIPS ’17), 6000–6010 (ACM, 2017).

  102. Wu, C. et al. Harnessing optoelectronic noises in a photonic generative network. Sci. Adv. 8, eabm2956 (2022).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  103. Bonnet, D. et al. Bringing uncertainty quantification to the extreme-edge with memristor-based Bayesian neural networks. Nat. Commun. 14, 7530 (2023).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  104. Olin-Ammentorp, W., Beckmann, K., Schuman, C. D., Plank, J. S. & Cady, N. C. Stochasticity and robustness in spiking neural networks. Neurocomputing 419, 23–36 (2021).

    Article  Google Scholar 

Download references

Acknowledgements

We thank J. Laydevant, M. Stein and M. Sohoni for helpful feedback on a draft of this manuscript. R.F. and A. Momeni acknowledge support from the Swiss National Science Foundation (SNSF) under the Eccellenza award 181232. R.F. and P.d.H. acknowledge support from the ANR-SNSF MINT project 212577 entitled ‘Ultra-compact non-linear metamaterial wave processors for analog deep learning’. P.L.M. acknowledges support from the National Science Foundation (award CCF-1918549) and a David and Lucile Packard Foundation Fellowship. N.G.B. acknowledges the support from the HORIZON EIC-2022-PATHFINDERCHALLENGES-01 HEISINGBERG project 101114978 and Weizmann-UK Make Connection grant 142568. S.G. is a member of the Institut Universitaire de France. T.O., L.G.W. and P.L.M. thank NTT Research for their financial and technical support. A.A. acknowledges support from the Department of Defense and the Simons Foundation. A. Skalli and D.B. acknowledge support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Consolidator Grant, grant agreement no. 101044777 (INSPIRE)).

Author information

Authors and Affiliations

  1. Laboratory of Wave Engineering, School of Electrical Engineering, Ècole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland

    Ali Momeni & Romain Fleury

  2. Microsoft Research, Cambridge, UK

    Babak Rahmani & Cheng Zhang

  3. Rain AI, San Francisco, CA, USA

    Benjamin Scellier

  4. Department of Applied Physics, Yale University, New Haven, CT, USA

    Logan G. Wright

  5. School of Applied and Engineering Physics, Cornell University, Ithaca, NY, USA

    Peter L. McMahon & Tatsuhiro Onodera

  6. Max Planck Institute for the Science of Light, Erlangen, Germany

    Clara C. Wanjura & Florian Marquardt

  7. Department of Electrical and Computer Engineering, University of California, Los Angeles, Los Angeles, CA, USA

    Yuhang Li & Aydogan Ozcan

  8. Université Marie et Louis Pasteur, CNRS UMR 6174, Institut FEMTO-ST, 25000, Besançon, France

    Anas Skalli & Daniel Brunner

  9. Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge, UK

    Natalia G. Berloff

  10. NTT Physics and Informatics Laboratories, NTT Research, Inc., Sunnyvale, CA, USA

    Tatsuhiro Onodera

  11. Laboratory of Applied Photonics Devices (LAPD), Ècole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland

    Ilker Oguz & Christophe Moser

  12. Dipartimento di Elettronica, Informazione e Bioingegneria, Politecnico di Milano, Milan, Italy

    Francesco Morichetti

  13. Université de Rennes, CNRS, IETR – UMR 6164, Rennes, France

    Philipp del Hougne

  14. IBM Research Europe – Zurich, Rüschlikon, Switzerland

    Manuel Le Gallo & Abu Sebastian

  15. Department of Computer Science, Stanford University, Stanford, CA, USA

    Azalia Mirhoseini

  16. Google DeepMind, Mountain View, CA, USA

    Azalia Mirhoseini

  17. Unité Mixte de Physique CNRS/Thales, CNRS, Thales, Université Paris-Saclay, Palaiseau, France

    Danijela Marković

  18. Laboratoire Kastler Brossel, Sorbonne Université, École Normale Supérieure, Collège de France, CNRS, Paris, France

    Sylvain Gigan

  19. Laboratoire Albert Fert, Laboratoire Albert Fert, CNRS, Thales, Université Paris-Saclay, Palaiseau, France

    Julie Grollier

  20. Department of Physics and Astronomy, University of Pennsylvania, Philadelphia, PA, USA

    Andrea J. Liu

  21. Optics Laboratory (LO), Ècole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland

    Demetri Psaltis

  22. Photonics Initiative, Advanced Science Research Center, City University of New York, New York, NY, USA

    Andrea Alù

  23. Physics Program, Graduate Center, City University of New York, New York, NY, USA

    Andrea Alù

Authors
  1. Ali Momeni
    View author publications

    Search author on:PubMed Google Scholar

  2. Babak Rahmani
    View author publications

    Search author on:PubMed Google Scholar

  3. Benjamin Scellier
    View author publications

    Search author on:PubMed Google Scholar

  4. Logan G. Wright
    View author publications

    Search author on:PubMed Google Scholar

  5. Peter L. McMahon
    View author publications

    Search author on:PubMed Google Scholar

  6. Clara C. Wanjura
    View author publications

    Search author on:PubMed Google Scholar

  7. Yuhang Li
    View author publications

    Search author on:PubMed Google Scholar

  8. Anas Skalli
    View author publications

    Search author on:PubMed Google Scholar

  9. Natalia G. Berloff
    View author publications

    Search author on:PubMed Google Scholar

  10. Tatsuhiro Onodera
    View author publications

    Search author on:PubMed Google Scholar

  11. Ilker Oguz
    View author publications

    Search author on:PubMed Google Scholar

  12. Francesco Morichetti
    View author publications

    Search author on:PubMed Google Scholar

  13. Philipp del Hougne
    View author publications

    Search author on:PubMed Google Scholar

  14. Manuel Le Gallo
    View author publications

    Search author on:PubMed Google Scholar

  15. Abu Sebastian
    View author publications

    Search author on:PubMed Google Scholar

  16. Azalia Mirhoseini
    View author publications

    Search author on:PubMed Google Scholar

  17. Cheng Zhang
    View author publications

    Search author on:PubMed Google Scholar

  18. Danijela Marković
    View author publications

    Search author on:PubMed Google Scholar

  19. Daniel Brunner
    View author publications

    Search author on:PubMed Google Scholar

  20. Christophe Moser
    View author publications

    Search author on:PubMed Google Scholar

  21. Sylvain Gigan
    View author publications

    Search author on:PubMed Google Scholar

  22. Florian Marquardt
    View author publications

    Search author on:PubMed Google Scholar

  23. Aydogan Ozcan
    View author publications

    Search author on:PubMed Google Scholar

  24. Julie Grollier
    View author publications

    Search author on:PubMed Google Scholar

  25. Andrea J. Liu
    View author publications

    Search author on:PubMed Google Scholar

  26. Demetri Psaltis
    View author publications

    Search author on:PubMed Google Scholar

  27. Andrea Alù
    View author publications

    Search author on:PubMed Google Scholar

  28. Romain Fleury
    View author publications

    Search author on:PubMed Google Scholar

Contributions

A. Momeni and R.F. conceived the overall idea and coordinated the project. The manuscript was structured into thematic sections, each contributed by different author groups: L.G.W., P.L.M., A. Momeni and R.F. contributed to the section on PNNs. L.G.W., P.L.M. and T.O. contributed to the section on physics-aware backpropagation training. A. Momeni, I.O., B.R., R.F., C.M. and D.P. contributed to the section on physical local learning. A. Skalli, D.B., S.G., A. Momeni and D.M. contributed to the sections on extreme learning machines, reservoir computing, feedback alignment and zeroth-order/gradient-free training. P.d.H. and N.G.B. contributed to the section on emerging technologies in PNNs. L.G.W., B.R., C.Z. and A. Mirhoseini contributed to the section on analogue-efficient large models. Y.L., A.O., M.L.G. and A. Sebastian contributed to the section on in silico training. B.S., C.C.W., F. Marquardt, A.J.L., F. Morichetti and J.G. contributed to the section gradient-descent training through physical dynamics. B.R., A. Momeni, P.L.M., A.A. and R.F. contributed to the introduction and outlook sections. All authors reviewed the manuscript and provided feedback and revisions to their respective sections. P.L.M. and L.G.W. provided further text, comments and feedback.

Corresponding author

Correspondence to Romain Fleury.

Ethics declarations

Competing interests

T.O., L.G.W. and P.L.M. are listed as inventors on a US provisional patent application (number 63/178,318) on physical neural networks and physics-aware training.

Peer review

Peer review information

Nature thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Information.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Momeni, A., Rahmani, B., Scellier, B. et al. Training of physical neural networks. Nature 645, 53–61 (2025). https://doi.org/10.1038/s41586-025-09384-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41586-025-09384-2

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics