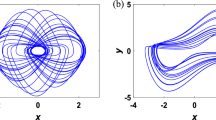
Abstract
This paper presents an adaptive control strategy for achieving anti-synchronization in transcendental alternated(odd and even functions) Julia sets. The system employs cosine-based transcendental mappings that works alternatively through iteration, generating complex Julia dynamics. Adaptive controllers are developed for both known and unknown set of parameters, with update laws incurred to estimate unknown coefficients of transcendental operators for the iterative schemes. Stability analysis of this article guarantees the convergence of the anti-synchronization error, while numerical results demonstrate rapid convergence and accurate parameter estimation of the control system. The article depicts the computational behavior of the system through the Average Number of Iterations (ANI) and time analysis, providing deeper insight into the convergence dynamics and efficiency of the iterative process. The proposed method enhances the stability and performance of transcendental alternated systems.
Similar content being viewed by others
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
References
Falconer, K.: Fractal geometry: mathematical foundations and applications, (John Wiley & Sons, 2013).
Julia, G. Mémoire sur l’itération des fonctions rationnelles. Journal de mathématiques pures et appliquées 1, 47–245 (1918).
de France, S. M. Bulletin de la Société mathématique de France, Vol. 1, La Société, (1875).
Sujitha, P., Konar, P. & Nathiya, N. A new iterative scheme for optimal convergence in equilibrium problems, Mathematical methods in the applied sciences (2025).
Pecora, L. M. & Carroll, T. L. Synchronization in chaotic systems. Physical review letters 64(8), 821 (1990).
Liao, T.-L. & Tsai, S.-H. Adaptive synchronization of chaotic systems and its application to secure communications. Chaos, Solitons & Fractals 11(9), 1387–1396 (2000).
Wang, P. & Liu, S. The gradient control of spatial-alternated julia sets. Nonlinear Dynamics 80(3), 1291–1302 (2015).
Wang, P. & Liu, S. Control of julia sets in generalized alternated system. Asian Journal of Control 18(6), 2234–2243 (2016).
Wang, P. & Zhang, H. Adaptive anti-synchronization of julia sets in generalized alternated system. IEEE Access 8, 175596–175601 (2020).
Wang, Y., Liu, S. & Li, H. Adaptive synchronization of julia sets generated by mittag-leffler function. Communications in Nonlinear Science and Numerical Simulation 83, 105115 (2020).
Zhang, Y.-P. Feedback control and synchronization of mandelbrot sets. Chinese Physics B 22(1), 010502 (2013).
Sun, W. & Zhang, Y. Control and synchronization of julia sets in the forced brusselator model. International Journal of Bifurcation and Chaos 25(09), 1550113 (2015).
Sun, W., Zhang, Y. & Zhang, X. Fractal analysis and control in the predator-prey model. International Journal of Computer Mathematics 94(4), 737–746 (2017).
Liu, X. & Hong, L. Chaos and adaptive synchronizations in fractional-order systems. International Journal of Bifurcation and Chaos 23(11), 1350175 (2013).
Chen, H., Liu, Y. & Lu, J. Synchronization criteria for two boolean networks based on logical control. International Journal of Bifurcation and Chaos 23(11), 1350178 (2013).
Zhang, Y. & Sun, W. Synchronization and coupling of mandelbrot sets. Nonlinear Dynamics 64(1), 59–63 (2011).
Prajapati, D. J., Rawat, S., Tomar, A., Sajid, M. & Dimri, R. A brief study on julia sets in the dynamics of entire transcendental function using mann iterative scheme. Fractal and Fractional 6(7), 397 (2022).
Alam, K. H. et al. An effective iterative process utilizing transcendental sine functions for the generation of julia and mandelbrot sets. Fractal and Fractional 9(1), 40 (2025).
Tassaddiq, A., Tanveer, M., Arshad, M., Alharbi, R. & Kasmani, R. M. Fractal generation and analysis using modified fixed-point iteration. AIMS Mathematics 10(4), 9462–9492 (2025).
Nandi, S., Al-Rawashdeh, A. & Konar, P. Non-linearity of the dynamics of transcendental function using fibonacci-mann iteration and some critical remarks. Alexandria Engineering Journal 117, 1–12 (2025).
Ravikumar, V. & Konar, P. Complex dynamics and fractals through viscosity approximation method with s-convexity, The European Physical Journal Special Topics 1–26 (2025).
Khan, A., Xie, W., Zhang, B. & Liu, L.-W. A survey of interval observers design methods and implementation for uncertain systems. Journal of the Franklin institute 358(6), 3077–3126 (2021).
Khan, A., Bai, X., Zhang, B. & Yan, P. Interval state estimator design for linear parameter varying (lpv) systems. IEEE Transactions on Circuits and Systems II: Express Briefs 68(8), 2865–2869 (2021).
Khan, A., Xie, W. & Liu, L.-W. Set-membership interval state estimator design using observability matrix for discrete-time switched linear systems. IEEE Sensors Journal 20(11), 6121–6129 (2020).
Masood, F., Ahmad, J., Shah, S. A., Jamal, S. S. & Hussain, I. A novel hybrid secure image encryption based on julia set of fractals and 3d lorenz chaotic map. Entropy 22(3), 274 (2020).
Gao, W., Sun, J., Qiao, W. & Zhang, X. Digital image encryption scheme based on generalized mandelbrot-julia set. Optik 185, 917–929 (2019).
Kaur, M. & Kumar, V. A comprehensive review on image encryption techniques. Archives of Computational Methods in Engineering, 27(1), (2020).
Funding
Open access funding provided by Vellore Institute of Technology. This research does not received any external funding.
Author information
Authors and Affiliations
Contributions
All authors made equal and substantial contributions to the conception, development, and completion of this work. V. R performed the methodology and computations. P.K conceptualized and supervised the findings of this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Ravikumar, V., Konar, P. Adaptive anti-synchronization of transcendental alternated system of Julia sets. Sci Rep (2026). https://doi.org/10.1038/s41598-026-36108-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-026-36108-x