Abstract
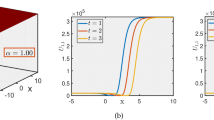
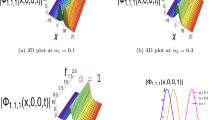
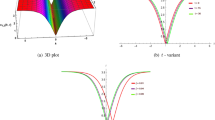
This research addresses the modified F-expansion, the newly established extended modified F-expansion, and the unified method for computing the exact solution of the time-fractional regularized long-wave (Tf-RLW) model with Conformable fractional derivative. The Tf-RLW model is widely applicable to solitary wave propagation in shallow water waves, plasma waves, and ion-acoustic waves. The three analytical techniques are employed to simplify this nonlinear model and justify the obtained waves in relation to the existing waves of this model. Fractional derivatives are non-integer-order operators widely used to model complex phenomena in science and engineering, with notable applications in ocean and coastal engineering for tsunami-wave mitigation. This research presented the bright-dark bell waves, periodic rogue waves, periodic waves, singular kink waves, and kinky-periodic bell waves as solutions to the governing model. 3-D, density, and 2-D sketches are given to analyze the intense behavior of the attained waves. Stability investigation of the obtained solutions is also included. All the solutions obtained in this research are substantiated using Maple 18.
Similar content being viewed by others
Data availability
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Ullah, M. S., Roshid, H. O., Ali, M. Z. & Rahman, Z. Novel exact solitary wave solutions for the time fractional generalized Hirota-Satsuma coupled KdV model through the generalized Kudryshov method. Contemp. Math. 1(1), 1–53 (2019).
Alshammari, F. S. et al. Dynamical structures of multi-solitons and interaction of solitons to the higher-order KdV-5 equation. Symmetry 15(3), 626 (2023).
Ananna, S. N., Mamun, A. A., Meia, M. A. A. & Lu, C. Chaotic behaviour, bifurcation, and stability analysis of the time-fractional phi-four model using the Hirota bilinear form. Int. J. Comput. Math. 102(12), 2146–2166 (2025).
Rahman, Z., Ali, M. Z., Roshid, H. O., Ullah, M. S. & Wen, X. Y. Dynamical structures of interaction wave solutions for the two extended higher-order KdV equations. Pramana. J. Phys. 95, 134 (2021).
Al-Amin, M., Islam, M. N. & Akbar, M. A. An improved modified simplest equation method for exact solitary wave solutions of the three-dimensional nonlinear fractional Wazwaz-Benjamin-Bona-Mahony model. Partial Differ. Equ. Appl. Math. 17, 101331 (2026).
Al-Amin, M., Islam, M. N. & Akbar, M. A. Computational analysis and wave propagation behavior of hyper-geometric soliton waves in plasma physics via the auxiliary equation method. Partial Differ. Equ. Appl. Math. 14, 101231 (2025).
Sheikh, M. A. N., Taher, M. A., Hossain, M. M., Akter, S. & Roshid, H. O. Variable coefficient exact solution of Sharma–Tasso–Olver model by enhanced modified simple equation method. PDEAM 7, 100527 (2023).
Jahan, M. I., Ullah, M. S., Roshid, H. O., Rahman, Z. & Akter, R. Novel dynamics of the Fokas-Lenells model in Birefringent fibers applying different integration algorithms. Int. J. Math. Comput. Eng. 3(1), 1–12 (2025).
Shahen, N. H. M. et al. On simulations of 3D fractional WBBM model through mathematical and graphical analysis with the assists of fractionality and unrestricted parameters. Sci. Rep. 14, 16420 (2024).
Patel, P. M. & Pradhan, V. H. A modified F-expansion method for solving nonlinear pseudo-parabolic BBMB equations. IOSR-JM 10(2), 18–25 (2014).
Aasaraai, A., Mehrlatifan, A. B. & Khaleghizadeh, S. Modified F-expansion method applied to coupled system of equation. J. Sci. I. R. 24(4), 347–354 (2013).
Hossain, M. M., Sheikh, M. A. N., Roshid, M. M., Roshid, H. O. & Taher, M. A. New soliton solutions and modulation instability analysis of the regularized long-wave equation in the conformable sense. PDEAM 9, 100615 (2024).
Hossain, M. M., Abdeljabbar, A., Roshid, H. O., Roshid, M. M. & Sheikh, M. A. N. Abundant bounded and unbounded solitary, periodic, rogue-type wave solutions and analysis of parametric effect on the solutions to nonlinear Klein-Gordon model. Complexity 2022, 8771583 (2022).
Mamun, A. A., Ananna, S. N. & Lu, C. Numerical investigation of bifurcation soliton, lump, and interaction solutions for the 3D fractional WBBM model using the Hirota bilinear form. Nonlinear Dyn. 113, 13631–13648 (2025).
Mamun, A. A., Ananna, S. N., Gharami, P. P., An, T. & Asaduzzaman, M. The improved modified extended tanh-function method to develop the exact travelling wave solutions of a family of 3D fractional WBBM equations. Result Phys. 41, 105969 (2022).
Alam, N. et al. Novel dynamics of the fractional KFG equation through the unified and unified solver schemes with stability and multistability analysis. Nonlin. Eng. 13(1), 20240034 (2024).
Mamun, A. A., Lu, C., Ananna, S. N. & Uddin, M. M. Dynamical behavior of water wave phenomena for the 3D fractional WBBM equations using rational sine-Gordon expansion method. Sci. Rep. 14, 6455 (2024).
Cao, N., Li, X. & Yin, X. The control model of Rossby waves and dynamic characteristics in stratified fluids. Chaos Soliton Fract. 201, 117208 (2025).
Alquran, M. Investigating the revisited generalized stochastic potential-Kdv equation: fractional time-derivative against proportional time-delay. Rom. J. Phys. 68, 106 (2023).
Alquran, M. The amazing fractional Maclaurin series for solving different types of fractional mathematical problems that arise in physics and engineering. PDEAM. 7, 100506 (2023).
Majid, S. Z., Asjad, M. I., Riaz, M. B. & Muhammad, T. Analyzing chaos and superposition of lump waves with other waves in the time-fractional coupled nonlinear schördinger equation. PLoS ONE 19(10), e0313333 (2024).
Majid, S. Z., Asjad, M. I., Kumar, S. & Muhammad, T. Dynamical study with exact travelling waves with high amplitude solitons to Clannish Random Walker’s parabolic equation. Qual. Theory Dyn. Syst. 24, 14 (2025).
Wang, K. J., Yan, K., Shi, F., Li, G. & Liu, X. Qualitative study of the (2+1)-dimensional BLMPE equation: Variational principle, Hamiltonian and diverse wave solutions. AIMS Math 10(11), 26168–26186 (2025).
Ullah, M. S., Hasan, M. & Mahbub, M. Analytical technique and diverse chaos-identifying tools for the time fractional symmetric regularized long wave equation. Sci Rep 16, 363 (2026).
Alam, N. et al. Bifurcation analysis, chaotic behaviors, and explicit solutions for a fractional two-mode Nizhnik-Novikov-Veselov equation in mathematical physics. AIMS Math. 10(3), 4558–4578 (2025).
Islam, M. N., Al-Amin, M. & Akbar, M. A. Abundant closed-form solitary solutions of a nonlinear neurobiological model for analyzing numerous signal transmission behaviors through the neuron using recent scheme. Partial Differ. Equ. Appl. Math. 13, 101051 (2025).
Al-Amin, M., Islam, M. N. & Akbar, M. A. Abundant distinct types of solitary wave solutions of the neurobiological model to analyze signal transmission behaviors through the neuron using recent scheme. Mod. Phys. Lett. B 39(13), 2450482 (2025).
Ullah, I. Dynamics behaviours of N-kink solitons in conformable Fisher–Kolmogorov–Petrovskii–Piskunov equation. Eng Comp 41(10), 2404–2426 (2024).
Shahen, N. H. M., Amin, M. A. & Foyjonnesa Rahman, M. M. Dynamics of computational waveform: A study of bifurcation, chaos, and sensitivity analysis. PLoS ONE 20(7), e0326230 (2025).
Hossain, M. M., Roshid, M. M., Sheikh, M. A. N., Taher, M. A. & Roshid, H. O. Novel exact soliton solutions of Cahn-Allen models with truncated m-fractional derivative. Int. J. Theor. Appl. Math. 8(6), 112–120 (2022).
Islam, B., Ali, M., Yeasmin, S., Akber, M. A. & Kumar, D. Exploring wave dynamics and disease progression in a fractional-order β-derivative multiple sclerosis model. AIP Adv. 15, 105217 (2025).
Ullah, I. et al. A novel approach is proposed for obtaining exact travelling wave solutions to the space-time fractional Phi-4 equation[J]. AIMS Math. 9(11), 32674–32695 (2024).
Ullah, I., Shah, K. & Abdeljawad, T. Study of traveling soliton and fronts phenomena in fractional Kolmogorov-Petrovskii-Piskunov equation. Phys. Scr. 99, 055259 (2024).
Eroğlu, B. B. I. Two-dimensional Cattaneo-Hristov heat diffusion in the half-plane. MMNSA. 3(3), 281–296 (2023).
Wang, K. J. & Xu, P. Generalized variational structure of the fractal modified Kdv–Zakharov–Kuznetsov equation. Fractals 31(7), 2350084 (2023).
Wang, K. J., Wang, G. D. & Shi, F. The pulse narrowing nonlinear transmission lines model within the local fractional calculus on the Cantor sets. COMPEL - Int. J. Comput. 42(6), 1576–1593 (2023).
Wang, K. J. The fractal active low-pass filter within the local fractional derivative on the Cantor set. COMPEL 42(6), 1396–1407 (2023).
Liang, Y. H. & Wang, K. J. Dynamics of the new exact wave solutions to the local fractional Vakhnenko-Parkes equation. Fractals 34(1), 2550102 (2026).
Wang, K. J. & Liu, J. H. On the zero state-response of the ℑ-order R-C circuit within the local fractional calculus. COMPEL 42(6), 1641–1653 (2022).
Alquran, M. Variation of the Influence of Atangana-conformable time-derivative on various physical structures in the fractional KP-BBM model. Int J Theor Phys. 63(9), 225 (2024).
Wang, K. J. Variational approach for the fractional exothermic reactions model with constant heat source in porous medium. Therm. Sci. 27(4A), 2879–2885 (2023).
Al-deiakeh, R. et al. Lie symmetry, convergence analysis, explicit solutions, and conservation laws for the time-fractional modified Benjamin-Bona-Mahony equation. J. Appl. Math. Comput. Mech. 23(1), 19–31 (2024).
Shahen, N. H. M., Foyjonnesa, B. & TahseenHossain, M. H. T. S. Solitary and rogue wave solutions to the conformable time fractional modified Kawahara equation in mathematical physics. Adv. Math. Phys. 2021, 6668092 (2021).
Majid, S. Z., Asjad, M. I. & Faridi, W. A. Formation of solitary waves solutions and dynamic visualization of the nonlinear schrödinger equation with efficient techniques. Phys. Scr. 99, 065255 (2024).
Shahen, N. H. M., Foyjonnesa, A. & Rahman, M. A. M. M. Soliton structures of fractional coupled Drinfel’d–Sokolov–Wilson equation arising in water wave mechanics. Sci Rep. 14, 18894 (2024).
Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 279, 57–66 (2015).
Khalil, R., Horani, M. A., Yousef, A. & Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 264, 65–70 (2014).
Noshad, M., Pishkoo, A. & Darus, M. Solving conformable fractional differential equations with “EJS” software and visualization of sub-diffusion process. Eur. J. Pure Appl. 15(4), 1738–1749 (2022).
Michal, P. & S˘kripkov´, P. L. Sturm’s theorems for conformable fractional differential equations. Math. Commun. 21, 273–281 (2016).
Jhangeer, A., Muddassar, M., Kousar, M. & Infal, B. Multistability and dynamics of fractional regularized long wave equation with conformable fractional derivatives. Ain Shams Eng. J. 12(2), 2153–2169 (2021).
Alam, N., Ma, W. X., Ullah, M. S., Seadawy, A. R. & Akter, M. Exploration of soliton structures in the Hirota-Maccari system with stability analysis. Mod. Phys. Lett. B. 39(11), 2450481 (2025).
Ullah, M. S. & Akter, R. Soliton dynamics and stability analysis of a double-chain DNA model with various chaos detection tools. Sci Rep 16, 1164 (2026).
Ejaz, S. T., Qamar, S. A., Akgül, A. & Hassani, M. K. Subdivision collocation method for numerical treatment of regularized long wave (RLW) equation. AIP Adv. 14, 015221 (2024).
Hossain, S., Roshid, M. M., Uddin, M., Ripa, A. A. & Roshid, H. O. Abundant time-wavering solutions of a modified regularized long wave model using the EMSE technique. PDEAM. 8, 100551 (2023).
Dag, I., Hepson, O.E. & Saka, B. A higher-order efficient approach to numerical simulations of the RLW equation. Pramana – J. Phys. 96, 30 (2022).
Shah, N. A., El-Zahar, E. R., Akgül, A., Khan, A. & Kafle, J. Analysis of fractional-order regularized long-wave models via a novel transform. J. Funct. Spaces. 2022, 2754507 (2022).
Yavuz, M., Sulaiman, T. A., Usta, F. & Bulut, H. Analysis and numerical computations of the fractional regularized long-wave equation with damping term. Math. Meth. Appl. Sci. 2020, 1–18 (2020).
Hassan, A.F., Ismail, H. N. A. & Elnaggara, K.M. A Restrictive Padé approximation for the solution of RLW equation. Int. J. Adv. Appl. Math. And Mech. 5(1), 7 – 14 (2017).
Aminikhaha, H., Sheikhani, A. H. R. & Rezazadeh, H. Sub-equation method for the fractional regularized long-wave equations with conformable fractional derivatives. Sci. Iran. B. 23(3), 1048–1054 (2016).
Hosseini, M.M., Ghaneai, H., Mohyud-Din, S.T. & Usman, M. Tri-prong scheme for regularized long wave equation. J. Assoc. Arab. Univ. Basic Appl. Sci. 20, 68–77 (2016).
Funding
No funding was received for this work.
Author information
Authors and Affiliations
Contributions
Mohammad Mobarak Hossain: conceptualization, visualization, software, methodology, data-curation, writing – original draft. Harun-Or-Roshid: formal analysis, validation, methodology, writing – review and editing. Mohammad Safi Ullah: formal analysis, review – original draft. Md. Abu Naim Sheikh: resources, investigation, validation.
Corresponding authors
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Hossain, M.M., Roshid, HO., Ullah, M.S. et al. Formation of advanced soliton dynamics through the M-fractional regularized long-wave equation. Sci Rep (2026). https://doi.org/10.1038/s41598-026-37284-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-026-37284-6