Abstract
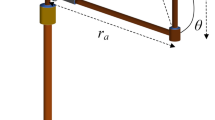
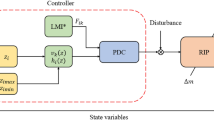
This study handles the robust sampled-data \(H_\infty\) fuzzy control analysis for a category of nonlinear partial differential systems (NPDSs) holding disturbances. As for now, the Takagi-Sugeno (T–S) fuzzy model serves superior by describing a broad category of nonlinear systems, and therefore, originally, a T–S fuzzy model is employed to illustrate the nonlinear parabolic partial differential systems. Here, the primary focus of this research is on designing a resilient sampled-data \(H_\infty\) fuzzy estimator-based controller which is competent in stabilizing the T–S fuzzy closed-loop partial differential systems (PDSs) and to tolerate the disruption under a specified level. By the virtue of Lyapunov stability theory, Green’s formula and several inequality techniques, the robust stabilization design problem based on a sampled-data fuzzy \(H_\infty\) estimator is effectively addressed using a set of linear matrix inequalities (LMIs). Moreover, the impacts of the diffusion phenomenon and the designed controller are clearly reflected in the derived criteria. Further, the acquired criteria can be checked for their practicability by the virtue of MATLAB LMI control toolbox. Finally, simulation results are presented to demonstrate the effectiveness of the proposed criteria.
Similar content being viewed by others
Data availability
No datasets were generated or analysed during the current study.
References
Ali, T. A., & Cacace, F. Finite dimensional observer design for a class of ODE-PDE systems involving delay. In 2025 American Control Conference (ACC), 1107-1112 (IEEE, 2025).
Qiu, Z. C. & Liu, Y. H. Visual feedback vibration control of flexible hinged plate system based on reinforcement learning algorithm. Mech. Syst. Signal Process.224, 112005 (2025).
Sassano, M. & Mylvaganam, T. Finite-dimensional characterization of optimal control laws over an infinite horizon for nonlinear systems. IEEE Trans. Autom. Control68(10), 5954–5965 (2022).
Chen, W.-H., Chen, B.-S. & Zhang, W. Robust control design for nonlinear stochastic partial differential systems with Poisson noise: Fuzzy implementation. Fuzzy Sets Syst.254, 83–105 (2014).
Christofides, P. D. Nonlinear and Robust Control of PDE Systems: Methods and Applications to Transport-Reaction Processes (Birkhauser, 2001).
Curtain, R. F. Finite-dimensional compensator design for parabolic distributed systems with point sensors and boundary input. IEEE Trans. Autom. Control27, 98–104 (1982).
Nasiri, N., Fakharian, A. & Menhaj, M. B. Observer-based robust control for flexible-joint robot manipulators: A state-dependent Riccati equation-based approach. Trans. Inst. Meas. Control42(16), 3135–3155 (2020).
Chen, Y. Y., Chang, Y.-T. & Chen, B.-S. Fuzzy solutions to partial differential equations: Adaptive approach. IEEE Trans. Fuzzy Syst.17, 116–127 (2009).
Wu, H.-N. & Li, H.-X. \(H_\infty\) fuzzy observer-based control for a class of nonlinear distributed parameter systems with control constraints. IEEE Trans. Fuzzy Syst.16, 502–516 (2008).
Yuan, K., Li, H.-X. & Cao, J. Robust stabilization of the distributed parameter system with time delay via fuzzy control. IEEE Trans. Fuzzy Syst.16, 567–584 (2008).
Chen, B.-S. & Chang, Y.-T. Fuzzy state-space modeling and robust observer-based control design for nonlinear partial differential systems. IEEE Trans. Fuzzy Syst.17, 1025–1043 (2009).
Wang, J. W., Wu, H. N. & Li, H.-X. Distributed proportional-spatial derivative control of nonlinear parabolic PDE systems via fuzzy PDE modeling approach. IEEE Trans. Syst., Man, Cybern. B, Cybern.42, 927–938 (2012).
Aslam, M. S. & Li, Q. Quantized dissipative filter design for Markovian switch T–S fuzzy systems with time-varying delays. Soft Comput. Fusion of Found. Methodol. Appl.23, 9876–9887 (2019).
Aslam, M. S. & Ma, Z. Output regulation for time-delayed Takagi-Sugeno fuzzy model with networked control system. Hacettepe J. Math. Stat.52, 1282–1302 (2023).
Li, Y., Zhang, H., Zhang, T. & Geng, H. Interval stability/stabilization and \(H_\infty\) feedback control for linear impulsive stochastic systems. Appl. Math. Comput.437, 127552 (2023).
Zheng, Y. & Zhang, G. \(H_ {\infty }\) state feedback control for nonlinear systems with input saturation based on policy iteration. In 2021 33rd Chinese Control and Decision Conference, 5894–5899 (IEEE, 2021).
Chen, H., Long, X., Tang, Y. & Xu, R. wPassive and \(H_{\infty }\) control based on non-fragile observer for a class of uncertain nonlinear systems with input time-delay. J. Vib. Control30(15–16), 3388–3401 (2024).
Wang, X. Y., Chang, X. H. & Liu, X. M. \(H_{\infty }\) control of nonlinear networked cascade control system under multi-channel quantization and event-triggered mechanism. Circuits, Syst. Signal Process.44(4), 2384–2405 (2025).
Zhuang, G., Xia, J., Feng, J. E., Wang, Y. & Chen, G. Dynamic compensator design and \(H_\infty\) admissibilization for delayed singular jump systems via Moore-Penrose generalized inversion technique. Nonlinear Anal. Hybrid Syst.49, 101361 (2023).
Vadivel, R., Njitacke, Z. T., Shanmugam, L., Hammachukiattikul, P. & Gunasekaran, N. Dynamical analysis and reachable set estimation of T–S fuzzy system with permanent magnet synchronous motor. Commun. Nonlinear Sci. Numer. Simul.125, 107407 (2023).
Wu, H.-N., Wang, J.-W. & Li, H.-X. Design of distributed \(H_\infty\) fuzzy controllers with constraint for nonlinear hyperbolic PDE systems. Automatica48, 2535–2543 (2012).
Sun, X., Zhang, C., Zhang, H. & Wang, F. Observer-based \(H_{\infty }\) fuzzy control for nonlinear parabolic PDE systems with matched and mismatched disturbances. Asian J. Control7, 1. https://doi.org/10.1002/asjc.3729 (2025).
Fridman, E. & Orlov, Y. An LMI approach to \(H_\infty\) boundary control of semilinear parabolic and hyperbolic systems. Automatica45, 2060–2066 (2009).
Chang, Y.-T., Ho, S.-J. & Chen, B.-S. Robust stabilization design of nonlinear stochastic partial differential systems: Fuzzy approach. Fuzzy Sets Syst.248, 61–85 (2014).
Zhang, X. M. & Wu, H. N. Estimator-based \(H_{\infty }\) boundary control for semilinear Itô-type stochastic parabolic partial differential systems. IFAC-PapersOnLine59(8), 214–219 (2025).
Ganeshan, P. & Dharani, S. Synchronization analysis of semi-Markovian jumping dual inertial fractional-order neural networks with time varying and proportional delay via quantized aperiodic intermittent control. Circuits Syst. Signal Process.4, 1–30. https://doi.org/10.1007/s00034-025-03367-4 (2025).
Aslam, M. S., Qaisar, I., Majid, A. & Ramaraj, P. Design of sliding mode controller for sensor/actuator fault with unknown input observer for satellite control system. Soft Comput.25, 14993–15003 (2021).
Aslam, M. S. et al. Formation control of heterogeneous multi-agent systems under fixed and switching hierarchies. IEEE Access12, 97868–97882 (2024).
Narenshakthi, T. & Dharani, S. Truncated predictive control for delayed networked control systems under dual attacks. Int. J. Dyn. Control13, 1–10 (2025).
Dharani, S., Rakkiyappan, R. & Cao, J. Robust stochastic sampled-data \(H_{\infty }\) control for a class of mechanical systems with uncertainties. J. Dyn. Syst. Meas. Control137(10), 90 (2015).
Sivaranjani, K., Sivakumar, M., Dharani, S., Loganathan, K. & Ngmgyel, N. Nonfragile synchronization of semi-Markovian jumping neural networks with time delays via sampled-data control and application to chaotic systems. J. Math.1, 2562227 (2021).
Ge, C., Chang, C., Liu, Y. & Liu, C. Sampled-data-based exponential synchronization of switched coupled neural networks with unbounded delay. Commun. Nonlinear Sci. Numer. Simul.117, 106931 (2023).
Wu, H. N. & Wang, Z. P. Observer-Based \(H_ {\infty }\) sampled-data fuzzy control for a class of nonlinear parabolic PDE systems. IEEE Trans. Fuzzy Syst.26(2), 454–473 (2017).
Kashkynbayev, A. & Rakkiyappan, R. Sampled-data output tracking control based on T–S fuzzy model for cancer-tumor-immune systems. Commun. Nonlinear Sci. Numer. Simul.128, 107642 (2024).
Liu, W., Lim, C.-C., Shi, P. & Xu, S. Sampled-data fuzzy control for a class of nonlinear systems with missing data and disturbances. Fuzzy Sets Syst.306, 63–86 (2017).
Dong, S., Zhu, H., Zhong, S., Shi, K. & Zhang, Z. Sampled-data stabilization analysis of neural-network-based control systems: A discontinuous bilateral looped-functional approach. Commun. Nonlinear Sci. Numer. Simul.111, 106446 (2022).
Dong, G. Nonlinear Partial Differential Equations of Second Order (American Mathematical Society, 1991).
Takagi, T. & Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst., Man, Cybern., Part-B15, 116–132 (1985).
Gu, K., Kharitonov, V. L. & Chen, J. Stability of Time-Delay Systems (Birkhauser, 2003).
Lu, L., Xing, Z. & He, B. Non-uniform sampled-data control for stochastic passivity and passification of Markov jump genetic regulatory networks with time-varying delays. Neurocomputing171, 434–443 (2016).
Boyd, S., Ghaoui, L. E., Feron, E. & Balakrishnan, V. Linear matrix inequalities in system and control theory (SIAM, 1994).
Murray, J. D. Mathematical Biology I: An Introduction (Springer, 2002).
Murray, J. D. Mathematical Biology II: Spatial Models and Biomedical Applications (Springer, 2003).
Shanks, N. Modeling biological systems: the Belousov-Zhabotinsky reaction. Found. Chem.3, 33–53 (2001).
Aslam, M. S., Chen, Z. & Zhang, B. Event-triggered fuzzy filtering in networked control system for a class of non-linear system with time delays. Int. J. Syst. Sci.49, 1587–1602 (2018).
Narenshakthi, T. & Dharani, S. Hybrid-triggered control for uncertain networked control system with time-varying delay and DoS attacks via two-sided looped functional. Complex Anal. Oper. Theory19, 206 (2025).
Narenshakthi, T. & Dharani, S. Extended dissipative truncated predictive control strategy for conic-type delayed networked control systems affected by cyber attacks and sensor distortion. Sci. Rep.16, 1238 (2025).
Acknowledgements
The authors are immensely grateful to the anonymous referees for the careful reading of this manuscript and helpful comments, which have been very useful for improving the quality of this manuscript.
Funding
Open access funding provided by Vellore Institute of Technology. The authors declare that no specific funding was received for this research.
Author information
Authors and Affiliations
Contributions
M. Sivakumar: Conceptualization, Methodology, Validation, Visualization, Writing - original draft. S. Dharani: Conceptualization, Formal analysis, Resources, Supervision, Writing - original draft, Writing - Review & Editing. Jinde Cao : Supervision, Review.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Sivakumar, M., Dharani, S. & Cao, J. Sampled-data fuzzy \(H_\infty\) estimators for control of nonlinear parabolic partial differential equations. Sci Rep (2026). https://doi.org/10.1038/s41598-026-37959-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-026-37959-0