Abstract
Accurate parameter identification in chaotic dynamical systems constitutes a challenging inverse problem due to extreme sensitivity to initial conditions, pronounced nonlinearity, and highly multimodal error landscapes. To address these challenges, this study proposes a global-best-guided electric eel foraging optimization algorithm (g-EEFO), which enhances the original EEFO framework by embedding a behavior-aware and phase-dependent global learning mechanism. Unlike existing EEFO variants that rely solely on stochastic foraging dynamics, g-EEFO integrates global-best information as a soft cooperative signal that modulates the interacting, resting, hunting, and migrating behaviors without overriding them. In this way, global guidance acts as a directional bias rather than a dominant attractor, preserving ecological diversity while strengthening convergence coherence. For the first time, EEFO and its improved variant are applied to chaotic system parameter estimation. The proposed method is evaluated on two representative models: the classical Lorenz system and a structurally richer memristive chaotic system. Extensive numerical experiments, including statistical analysis, convergence profiling, boxplot distributions, and parameter-evolution trajectories, demonstrate the clear superiority of g-EEFO over several state-of-the-art metaheuristics. For the Lorenz system, g-EEFO achieves a best mean squared error of \(\:7.02\times\:{10}^{-26}\), which is six to twenty orders of magnitude lower than competing methods, while maintaining an exceptionally small standard deviation (\(\:4.58\times\:{10}^{-20}\)). For the memristive system, g-EEFO attains a best error of \(\:8.19\times\:{10}^{-19}\), again outperforming all benchmarks by several orders of magnitude and exhibiting the highest run-to-run stability. In both cases, the estimated parameters match the true system values with near-perfect precision. These results confirm that the proposed behavior-aware global guidance fundamentally reshapes the search dynamics of EEFO, yielding substantial gains in convergence stability, numerical accuracy, and robustness. The g-EEFO therefore provides a powerful and reliable alternative for chaotic parameter identification and nonlinear system reconstruction across diverse dynamical regimes.
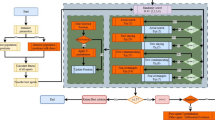
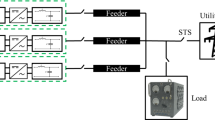
Similar content being viewed by others
Data availability
All related data are presented within the manuscript.
References
Modares, H., Alfi, A. & Fateh, M. M. Parameter identification of chaotic dynamic systems through an improved particle swarm optimization. Expert Syst. Appl. 37, 3714 (2010).
Wang, L., Xu, Y. & Li, L. Parameter identification of chaotic systems by hybrid Nelder-Mead simplex search and differential evolution algorithm. Expert Syst. Appl. 38, 3238–3245 (2011).
Deng, L. & Liu, S. A sine cosine algorithm guided by elite pool strategy for global optimization. Appl. Soft Comput. 164, 111946 (2024).
Deng, L. & Liu, S. Snow ablation optimizer: A novel metaheuristic technique for numerical optimization and engineering design. Expert Syst. Appl. 225, 120069 (2023).
Deng, L. & Liu, S. A multi-strategy improved slime mould algorithm for global optimization and engineering design problems. Comput. Methods Appl. Mech. Eng. 404, 115764 (2023).
Deng, L. & Liu, S. An enhanced slime mould algorithm based on adaptive grouping technique for global optimization. Expert Syst. Appl. 222, 119877 (2023).
Deng, L. & Liu, S. Incorporating Q-learning and gradient search scheme into JAYA algorithm for global optimization. Artif. Intell. Rev. 56, 3705–3748 (2023).
Deng, L., Liu, S. A. & Novel Hybrid Grasshopper optimization algorithm for numerical and engineering optimization problems. Neural Process. Lett. 55, 9851–9905 (2023).
Deng, L. & Liu, S. Advancing photovoltaic system design: an enhanced social learning swarm optimizer with guaranteed stability. Comput. Ind. 164, 104209 (2025).
Ahmadi, M. & Mojallali, H. Chaotic invasive weed optimization algorithm with application to parameter Estimation of chaotic systems. Chaos Solitons Fractals. 45, 1108–1120 (2012).
Li, C., Zhou, J., Xiao, J. & Xiao, H. Parameters identification of chaotic system by chaotic gravitational search algorithm. Chaos Solitons Fractals. 45, 539–547 (2012).
Lin, J. & Chen, C. Parameter Estimation of chaotic systems by an oppositional seeker optimization algorithm. Nonlinear Dyn. 76, 509–517 (2014).
Lazzús, J. A., Rivera, M. & López-Caraballo, C. H. Parameter Estimation of Lorenz chaotic system using a hybrid swarm intelligence algorithm. Phys. Lett. Sect. A: Gen. At. Solid State Phys. 380, 1164–1171 (2016).
Zhang, H. et al. Parameter Estimation of nonlinear chaotic system by improved TLBO strategy. Soft comput. 20, 4965–4980 (2016).
Mousavi, Y. & Alfi, A. Fractional calculus-based firefly algorithm applied to parameter Estimation of chaotic systems. Chaos Solitons Fractals. 114, 202–215 (2018).
Anh, H. P. H., Son, N. N. & Van Kien, C. Ho-Huu, V. Parameter identification using adaptive differential evolution algorithm applied to robust control of uncertain nonlinear systems. Appl. Soft Comput. J. 71, 672–684 (2018).
Ding, Z. H., Lu, Z. R. & Liu, J. K. Parameters identification of chaotic systems based on artificial bee colony algorithm combined with cuckoo search strategy. Sci. China Technol. Sci. 61, 417–426 (2017).
Turgut, M. S., Sağban, H. M., Turgut, O. E. & Özmen, Ö. T. Whale optimization and sine–cosine optimization algorithms with cellular topology for parameter identification of chaotic systems and Schottky barrier diode models. Soft comput. 25, 1365–1409 (2021).
Nuñez-Perez, J. C. et al. Maximizing the chaotic behavior of fractional order Chen system by evolutionary algorithms. Math. 2021. 9, 1194 (2021).
Zainel, Q. M., Darwish, S. M. & Khorsheed, M. B. Employing quantum fruit fly optimization algorithm for solving Three-Dimensional chaotic equations. Math. 2022. 10, Page 4147 (10), 4147 (2022).
Rizk-Allah, R. M., Farag, M. A., Barghout, M. H. & Hassanien, A. E. A Memory-Based particle swarm optimization for parameter identification of Lorenz chaotic system. Lecture Notes Networks Syst. 394, 571–587 (2022).
Sattar, D. & Shehadeh Braik, M. Metaheuristic methods to identify parameters and orders of fractional-order chaotic systems. Expert Syst. Appl 228 (2023).
Kumar, K. Data-driven modeling and parameter estimation of nonlinear systems. Eur. Phys. J. B 96, 1–13 (2023).
Nathasarma, R. & Roy, B. K. Physics-Informed Long-Short-Term memory neural network for parameters Estimation of nonlinear systems. IEEE Trans. Ind. Appl. 59, 5376–5384 (2023).
Cavlak, Y., Ateş, A., Abualigah, L. & Elaziz, M. A. Fractional-order chaotic oscillator-based Aquila optimization algorithm for maximization of the chaotic with Lorentz oscillator. Neural Comput. Appl. 35, 21645–21662 (2023).
Farjami, A. A. & Yaghoobi, M. Kardehi Moghaddam, R. Extended cascade chaotic systems and Estimation parameters with new chaotic grey Wolf algorithm. J. Experimental Theoretical Artif. Intell. 36, 1187–1211 (2024).
Ahmadi, A. et al. A novel megastable chaotic system with hidden attractors and its parameter Estimation using the sparrow search algorithm. Comput. 2024. 12, 245 (2024).
Wu, G. C., Wu, Z. Q. & Zhu, W. Data-driven discrete fractional chaotic systems, new numerical schemes and deep learning. Chaos 34 (2024).
Lin, K., Han, X., Xu, X., Zong, T. & Zhou, X. Parameter estimation of fractional-order chaotic system based on adaptive artificial evolutionary fish swarm algorithm. Proceedings of IEEE 14th Data Driven Control and Learning Systems Conference, DDCLS 2025 739–744 (2025). https://doi.org/10.1109/DDCLS66240.2025.11066043
Kumar, K. & Kostina, E. Machine learning in parameter Estimation of nonlinear systems. Eur. Phys. J. B 2025. 98:4 98, 1–18 (2025).
Zhao, W. et al. Electric eel foraging optimization: A new bio-inspired optimizer for engineering applications. Expert Syst. Appl 238 (2024).
Mehta, P., Yildiz, B. S., Sait, S. M. & Ylldlz, A. R. Optimization of electric vehicle design problems using improved electric eel foraging optimization algorithm. Materialpruefung/Materials Test. 66, 1230–1240 (2024).
Abdelwahab, S. A. M. et al. Optimal control and optimization of Grid-Connected PV and wind turbine hybrid systems using electric eel foraging optimization algorithms. Sens. 2024. 24, 2354 (2024).
Al-qaness, M. A. A. et al. Optimized quantum LSTM using modified electric eel foraging optimization for real-world intelligence engineering systems. Ain Shams Eng. J. 15, 102982 (2024).
Ebrahim, M. A., Ragab, A. S., Aziz, B. A. & AbdelHadi, H. A. Electric Eel foraging optimization based control design of islanded microgrid. Sci. Rep. 15, 1–22 (2025).
Rezk, H., Ghasemi, M., Al Saadi, A. & Sayed, E. T. Experimental validation of single and multi-objective optimization of microbial fuel cell based on recent electric eel foraging algorithm. Energy 339, 138989 (2025).
Ekinci, S. Nonlinear controller design for automotive engine speed regulation utilizing electric eel foraging optimization. Int J. Dyn. Control 13 (2025).
Abdel-salam, M., Houssein, E. H., Emam, M. M., Abdel Samee, N. & Azam, M. T. A novel dynamic Nelder-based electric eel foraging algorithm for global optimization and pathological colorectal cancer image segmentation. Comput. Biol. Med. 197 (2025).
Mehmood, K. et al. Design of chaos induced Aquila optimizer for parameter estimation of electro-hydraulic control system. Comput. Model. Eng. Sci. 143, 1809–1841 (2025).
Mehmood, K. et al. Design of chaotic young’s double Slit experiment optimization heuristics for identification of nonlinear muscle model with key term separation. Chaos Solitons Fractals. 189, 115636 (2024).
Wang, X. Gyro fireworks algorithm: A new metaheuristic algorithm. AIP Adv. 14 (2024).
Wang, X. Bighorn sheep optimization algorithm: a novel and efficient approach for wireless sensor network coverage optimization. Phys. Scr. 100, 075230 (2025).
Wang, X. & Yao, L. Cape Lynx optimizer: A novel metaheuristic algorithm for enhancing wireless sensor network coverage. Measurement 256, 118361 (2025).
Wang, R. et al. The animated oat optimization algorithm: A nature-inspired metaheuristic for engineering optimization and a case study on wireless sensor networks. Knowl. Based Syst. 318 (2025).
Lang, Y. & Gao, Y. Dream optimization algorithm (DOA): A novel metaheuristic optimization algorithm inspired by human Dreams and its applications to real-world engineering problems. Comput Methods Appl. Mech. Eng 436 (2025).
Yuan, Y. et al. Musk ox optimizer (MO): A novel optimization algorithm and its application. Clust. Comput. 28 (2025).
Han, M. et al. Walrus optimizer: A novel nature-inspired metaheuristic algorithm. Expert Syst. Appl. 239 (2024).
Xiong, Q., Shen, J., Tong, B. & Xiong, Y. Parameter identification for memristive chaotic system using modified sparrow search algorithm. Front. Phys. 10, 912606 (2022).
Abualigah, L. et al. Optimized image segmentation using an improved reptile search algorithm with Gbest operator for multi-level thresholding. Sci. Rep. 15, 1–45 (2025).
Lorenz, E. N. Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–141 (1963).
McKnight, P. E., Najab, J., Mann-Whitney, U. & Test Corsini Encycl. Psychol. 1–1 https://doi.org/10.1002/9780470479216.CORPSY0524. (2010).
Chang, J. F., Yang, Y. S., Liao, T. L. & Yan, J. J. Parameter identification of chaotic systems using evolutionary programming approach. Expert Syst. Appl. 35, 2074–2079 (2008).
Li, X. T. & Yin, M. H. Parameter Estimation for chaotic systems using the cuckoo search algorithm with an orthogonal learning method. Chin. Phys. B 21 (2012).
Ekinci, S., Turkeri, C., Izci, D., Kiselychnyk, O. & Gunes, B. B. Opposition-based starfish optimization algorithm for function optimization. 9th International Artificial Intelligence and Data Processing Symposium (IDAP) 1–4 (2025).https://doi.org/10.1109/IDAP68205.2025.11222186
Xiong, Q., She, J. & Xiong, J. A. New pelican optimization algorithm for the parameter identification of memristive chaotic system. Symmetry 2023. 15, 1279 (2023).
Funding
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Author information
Authors and Affiliations
Contributions
Davut Izci, Serdar Ekinci: Conceptualization, Methodology, Software, Visualization, Investigation, Writing- Original draft preparation, İrfan Ökten, Vedat Tümen, Burcu Bektaş Güneş, Mostafa Rashdan, Mohammad Salman: Data curation, Validation, Supervision, Resources, Writing - Review & Editing, Writing - Review & Editing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Izci, D., Ekinci, S., Ökten, İ. et al. Global-best-guided electric eel foraging optimizer for robust parameter identification of Lorenz and memristive chaotic systems. Sci Rep (2026). https://doi.org/10.1038/s41598-026-39729-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-026-39729-4