Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Primer
  • Published:

Quantum imaging with correlated photon pairs

Nature Reviews Methods Primers volume 6, Article number: 17 (2026) Cite this article

Subjects

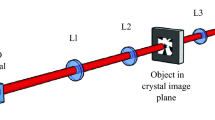
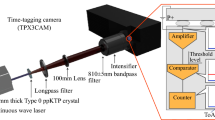
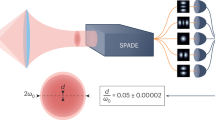
Abstract

Quantum imaging encompasses many techniques, from the use of cameras that detect single photons with picosecond temporal resolution, to the use of nonlinear materials to create pairs of photons correlated over many different degrees of freedom, or even utilizing the interference between two of these photon-pair sources. This article focuses on the various imaging techniques using correlations between photon pairs, reviews the basic theory required to understand the method, discusses the practicalities of implementing these approaches, presents ways in which such systems might surpass classical limits and considers the applications that these advances might enable. Finally, we discuss future directions of the field of quantum imaging and the challenges that remain, both in terms of required new technologies and areas of physics in which our understanding may be incomplete.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: The various forms of quantum imaging.
Fig. 2: Image plane and far-field correlations.
Fig. 3: Quantum ghost imaging configurations and their classical analogues.
Fig. 4: Alignment and image planes.
Fig. 5: Projective masks.
Fig. 6: Machine intelligence-enhanced quantum imaging.
Fig. 7: Applications of quantum imaging.

Similar content being viewed by others

References

  1. Strekalov, D., Sergienko, A., Klyshko, D. & Shih, Y. Observation of two-photon “ghost” interference and diffraction. Phys. Rev. Lett. 74, 3600 (1995).

    Article  ADS  Google Scholar 

  2. Pittman, T. B., Shih, Y., Strekalov, D. & Sergienko, A. V. Optical imaging by means of two-photon quantum entanglement. Phys. Rev. A 52, R3429 (1995). This work is one of the earliest demonstrations that spatial correlations in entangled photon pairs can be used to form an image, establishing the experimental foundation for what later became known as quantum ghost imaging.

    Article  ADS  Google Scholar 

  3. Pittman, T. et al. Two-photon geometric optics. Phys. Rev. A 53, 2804 (1996).

    Article  ADS  Google Scholar 

  4. Bennink, R. S., Bentley, S. J., Boyd, R. W. & Howell, J. C. Quantum and classical coincidence imaging. Phys. Rev. Lett. 92, 033601 (2004).

    Article  ADS  Google Scholar 

  5. Gatti, A., Brambilla, E., Bache, M. & Lugiato, L. A. Correlated imaging, quantum and classical. Phys. Rev. A 70, 013802 (2004). This paper establishes a theoretical framework for correlated light imaging, clarifying the connections and distinctions between quantum and classical schemes.

    Article  ADS  Google Scholar 

  6. Jedrkiewicz, O. et al. Detection of sub-shot-noise spatial correlation in high-gain parametric down conversion. Phys. Rev. Lett. 93, 243601 (2004).

    Article  ADS  Google Scholar 

  7. Morris, P. A., Aspden, R. S., Bell, J. E., Boyd, R. W. & Padgett, M. J. Imaging with a small number of photons. Nat. Commun. 6, 5913 (2015).

    Article  ADS  Google Scholar 

  8. Gatti, A., Brambilla, E., Bache, M. & Lugiato, L. A. Ghost imaging with thermal light: comparing entanglement and classical correlation. Phys. Rev. Lett. 93, 093602 (2004).

    Article  ADS  Google Scholar 

  9. Ferri, F. et al. High-resolution ghost image and ghost diffraction experiments with thermal light. Phys. Rev. Lett. 94, 183602 (2005).

    Article  ADS  Google Scholar 

  10. Valencia, A., Scarcelli, G., D’Angelo, M. & Shih, Y. Two-photon imaging with thermal light. Phys. Rev. Lett. 94, 063601 (2005).

    Article  ADS  Google Scholar 

  11. Aspden, R. S., Tasca, D. S., Boyd, R. W. & Padgett, M. J. EPR-based ghost imaging using a single-photon-sensitive camera. New J. Phys. 15, 073032 (2013). This work demonstrates Einstein–Podolsky–Rosen-based ghost imaging, showing that imaging with position correlations yields an upright image, whereas momentum correlations produce an inverted image, in direct analogy with classical lens systems.

    Article  ADS  Google Scholar 

  12. Meyers, R., Deacon, K. S. & Shih, Y. Ghost-imaging experiment by measuring reflected photons. Phys. Rev. A 77, 041801 (2008).

    Article  ADS  Google Scholar 

  13. Malik, M., Magaña-Loaiza, O. S. & Boyd, R. W. Quantum-secured imaging. Appl. Phys. Lett. 101, 241103 (2012).

    Article  ADS  Google Scholar 

  14. Aspden, R. S. et al. Photon-sparse microscopy: visible light imaging using infrared illumination. Optica 2, 1049–1052 (2015).

    Article  ADS  Google Scholar 

  15. Lloyd, S. Enhanced sensitivity of photodetection via quantum illumination. Science 321, 1463–1465 (2008).

    Article  ADS  Google Scholar 

  16. Brida, G., Genovese, M. & Ruo Berchera, I. Experimental realization of sub-shot-noise quantum imaging. Nat. Photonics 4, 227–230 (2010). This work presents an experimental realization of sub-shot-noise imaging, providing a clear demonstration of the potential for quantum advantage in signal-to-noise ratio.

    Article  ADS  Google Scholar 

  17. Defienne, H., Reichert, M., Fleischer, J. W. & Faccio, D. Quantum image distillation. Sci. Adv. 5, eaax0307 (2019).

    Article  ADS  Google Scholar 

  18. Gregory, T., Moreau, P.-A., Toninelli, E. & Padgett, M. J. Imaging through noise with quantum illumination. Sci. Adv. 6, eaay2652 (2020).

    Article  ADS  Google Scholar 

  19. Johnson, S., Rarity, J. & Padgett, M. Transmission of quantum-secured images. Sci. Rep. 14, 11579 (2024).

    Article  ADS  Google Scholar 

  20. D’Angelo, M., Chekhova, M. V. & Shih, Y. Two-photon diffraction and quantum lithography. Phys. Rev. Lett. 87, 013602 (2001).

    Article  ADS  Google Scholar 

  21. Tsang, M. Quantum imaging beyond the diffraction limit by optical centroid measurements. Phys. Rev. Lett. 102, 253601 (2009).

    Article  ADS  Google Scholar 

  22. Toninelli, E. et al. Resolution-enhanced quantum imaging by centroid estimation of biphotons. Optica 6, 347–353 (2019).

    Article  ADS  Google Scholar 

  23. Cameron, P. et al. Adaptive optical imaging with entangled photons. Science 383, 1142–1148 (2024). This study demonstrates adaptive optical imaging using entangled photons, showing how spatial correlations between photon pairs can be utilized to correct aberrations.

    Article  ADS  MathSciNet  Google Scholar 

  24. Lemos, G. B. et al. Quantum imaging with undetected photons. Nature 512, 409–412 (2014). This study introduces quantum imaging with undetected photons, showing that objects can be imaged at one wavelength while only detecting photons at a different wavelength, using interference between nonlinear crystals.

    Article  ADS  Google Scholar 

  25. Chekhova, M. & Ou, Z. Nonlinear interferometers in quantum optics. Adv. Opt. Photonics 8, 104–155 (2016).

    Article  ADS  Google Scholar 

  26. Caves, C. M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 23, 1693 (1981).

    Article  ADS  Google Scholar 

  27. Zou, X. Y., Wang, L. J. & Mandel, L. Induced coherence and indistinguishability in optical interference. Phys. Rev. Lett. 67, 318–321 (1991).

    Article  ADS  Google Scholar 

  28. Wang, L. J., Zou, X. Y. & Mandel, L. Induced coherence without induced emission. Phys. Rev. A 44, 4614–4622 (1991).

    Article  ADS  Google Scholar 

  29. Kviatkovsky, I., Chrzanowski, H. M., Avery, E. G., Bartolomaeus, H. & Ramelow, S. Microscopy with undetected photons in the mid-infrared. Sci. Adv. 6, eabd0264 (2020). This study extends undetected photon imaging to the mid-IR, demonstrating its applicability to microscopy with label-free molecular contrast, while relying solely on visible-wavelength detection.

    Article  ADS  Google Scholar 

  30. Brambilla, E., Gatti, A., Bache, M. & Lugiato, L. A. Simultaneous near-field and far-field spatial quantum correlations in the high-gain regime of parametric down-conversion. Phys. Rev. A 69, 023802 (2004).

    Article  ADS  Google Scholar 

  31. Moreau, P.-A. et al. Resolution limits of quantum ghost imaging. Opt. Express 26, 7528–7536 (2018).

    Article  ADS  Google Scholar 

  32. Boyd, R. W. Nonlinear Optics 4th edn (Academic, 2020).

  33. Schneeloch, J. & Howell, J. C. Introduction to the transverse spatial correlations in spontaneous parametric down-conversion through the biphoton birth zone. J. Opt. 18, 053501 (2016).

    Article  ADS  Google Scholar 

  34. Kviatkovsky, I., Chrzanowski, H. M. & Ramelow, S. Mid-infrared microscopy via position correlations of undetected photons. Opt. Express 30, 5916–5925 (2022).

    Article  ADS  Google Scholar 

  35. Howell, J. C., Bennink, R. S., Bentley, S. J. & Boyd, R. W. Realization of the Einstein-Podolsky-Rosen paradox using momentum- and position-entangled photons from spontaneous parametric down conversion. Phys. Rev. Lett. 92, 210403 (2004). This study provides one of the clearest experimental demonstrations of the Einstein–Podolsky–Rosen paradox using position-entangled and momentum-entangled photon pairs generated by SPDC.

    Article  ADS  Google Scholar 

  36. Jost, B. M., Sergienko, A. V., Abouraddy, A. F., Saleh, B. E. & Teich, M. C. Spatial correlations of spontaneously down-converted photon pairs detected with a single-photon-sensitive CCD camera. Opt. Express 3, 81–88 (1998).

    Article  ADS  Google Scholar 

  37. Fickler, R., Krenn, M., Lapkiewicz, R., Ramelow, S. & Zeilinger, A. Real-time imaging of quantum entanglement. Sci. Rep. 3, 1914 (2013).

    Article  ADS  Google Scholar 

  38. Aspden, R. S., Padgett, M. J. & Spalding, G. C. Video recording true single-photon double-slit interference. Am. J. Phys. 84, 671–677 (2016).

    Article  ADS  Google Scholar 

  39. Zhang, L., Neves, L., Lundeen, J. S. & Walmsley, I. A. A characterization of the single-photon sensitivity of an electron multiplying charge-coupled device. J. Phys. B At. Mol. Opt. Phys. 42, 114011 (2009).

    Article  ADS  Google Scholar 

  40. Moreau, P.-A., Devaux, F. & Lantz, E. Einstein-Podolsky-Rosen paradox in twin images. Phys. Rev. Lett. 113, 160401 (2014).

    Article  ADS  Google Scholar 

  41. Edgar, M. P. et al. Imaging high-dimensional spatial entanglement with a camera. Nat. Commun. 3, 984 (2012).

    Article  ADS  Google Scholar 

  42. Gregory, T., Moreau, P.-A., Mekhail, S., Wolley, O. & Padgett, M. Noise rejection through an improved quantum illumination protocol. Sci. Rep. 11, 21841 (2021).

    Article  ADS  Google Scholar 

  43. Lantz, E., Blanchet, J.-L., Furfaro, L. & Devaux, F. Multi-imaging and Bayesian estimation for photon counting with EMCCDs. Mon. Not. R. Astron. Soc. 386, 2262–2270 (2008).

    Article  ADS  Google Scholar 

  44. Roberts, K., Wolley, O., Gregory, T. & Padgett, M. A comparison between the measurement of quantum spatial correlations using qCMOS photon-resolving and electron multiplying CCD camera technologies. Sci. Rep. 14, 14687 (2024).

    Article  ADS  Google Scholar 

  45. Wolley, O., Gregory, T., Beer, S., Higuchi, T. & Padgett, M. Quantum imaging with a photon counting camera. Sci. Rep. 12, 8286 (2022).

    Article  ADS  Google Scholar 

  46. Portaluppi, D., Conca, E. & Villa, F. 32 × 32 CMOS SPAD imager for gated imaging, photon timing, and photon coincidence. IEEE J. Sel. Top. Quantum Electron. 24, 1–6 (2018).

    Article  Google Scholar 

  47. Ulku, A. C. et al. A 512 × 512 SPAD image sensor with integrated gating for widefield FLIM. IEEE J. Sel. Top. Quantum Electron. 25, 1–12 (2019).

    Article  Google Scholar 

  48. Henderson, R. K. et al. A 192 × 128 time correlated SPAD image sensor in 40-nm CMOS technology. IEEE J. Solid-State Circuits 54, 1907–1916 (2019).

    Article  ADS  Google Scholar 

  49. Ndagano, B. et al. Imaging and certifying high-dimensional entanglement with a single-photon avalanche diode camera. npj Quantum Inf. 6, 94 (2020).

    Article  ADS  Google Scholar 

  50. Hadfield, R. H. et al. Single-photon detection for long-range imaging and sensing. Optica 10, 1124–1141 (2023).

    Article  ADS  Google Scholar 

  51. Morozov, D. V., Casaburi, A. & Hadfield, R. H. Superconducting photon detectors. Contemp. Phys. 62, 69–91 (2021).

    Article  ADS  Google Scholar 

  52. Couteau, C. Spontaneous parametric down-conversion. Contemp. Phys. 59, 291–304 (2018).

    Article  ADS  Google Scholar 

  53. Boeuf, N. et al. Calculating characteristics of noncollinear phase matching in uniaxial and biaxial crystals. Opt. Eng. 39, 1016–1024 (2000).

    Article  ADS  Google Scholar 

  54. Morgan, R. A. & Hopf, F. A. Measurement of the temperature tuning coefficient of lithium niobate using nonlinear optical interferometry. Appl. Opt. 25, 3011_1–3013 (1986).

    Article  Google Scholar 

  55. Shen, Y. R. The Principles of Nonlinear Optics (Wiley, 1984).

  56. Klyshko, D. A simple method of preparing pure states of an optical field, of implementing the Einstein–Podolsky–Rosen experiment, and of demonstrating the complementarity principle. Sov. Phys. Usp. 31, 74 (1988).

    Article  ADS  Google Scholar 

  57. Shapiro, J. H. & Boyd, R. W. The physics of ghost imaging. Quantum Inf. Process. 11, 949–993 (2012).

    Article  ADS  Google Scholar 

  58. D’Angelo, M., Valencia, A., Rubin, M. H. & Shih, Y. Resolution of quantum and classical ghost imaging. Phys. Rev. A 72, 013810 (2005).

    Article  ADS  Google Scholar 

  59. Goodman, J. W. Introduction to Fourier Optics 3rd edn (Roberts and Company, 2005).

  60. Tasca, D. et al. The influence of non-imaging detector design on heralded ghost-imaging and ghost-diffraction examined using a triggered ICCD camera. Opt. Express 21, 30460–30473 (2013).

    Article  ADS  Google Scholar 

  61. Sheppard, C. J., Mehta, S. B. & Heintzmann, R. Superresolution by image scanning microscopy using pixel reassignment. Opt. Lett. 38, 2889–2892 (2013).

    Article  ADS  Google Scholar 

  62. Zhang, Y. et al. Interaction-free ghost-imaging of structured objects. Opt. Express 27, 2212–2224 (2019).

    Article  ADS  Google Scholar 

  63. Moodley, C. & Forbes, A. All-digital quantum ghost imaging: tutorial. J. Opt. Soc. Am. B 40, 3073–3095 (2023).

    Article  ADS  Google Scholar 

  64. Nape, I., Sephton, B., Ornelas, P., Moodley, C. & Forbes, A. Quantum structured light in high dimensions. APL Photonics 8, 051101 (2023).

    Article  ADS  Google Scholar 

  65. Boudoux, C. Fundamentals of Biomedical Optics (Blurb, 2023).

  66. Rubin, M. H. & Shih, Y. Resolution of ghost imaging for nondegenerate spontaneous parametric down-conversion. Phys. Rev. A 78, 033836 (2008).

    Article  ADS  Google Scholar 

  67. Moreau, P.-A. et al. Demonstrating an absolute quantum advantage in direct absorption measurement. Sci. Rep. 7, 6256 (2017).

    Article  ADS  Google Scholar 

  68. Hong, C.-K., Ou, Z.-Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044 (1987).

    Article  ADS  Google Scholar 

  69. Ndagano, B. et al. Quantum microscopy based on Hong–Ou–Mandel interference. Nat. Photonics 16, 384–389 (2022).

    Article  ADS  Google Scholar 

  70. Pepe, F. V., Di Lena, F., Garuccio, A., Scarcelli, G. & D’Angelo, M. Correlation plenoptic imaging with entangled photons. Technologies 4, 17 (2016).

    Article  Google Scholar 

  71. Zhang, Y., England, D., Orth, A., Karimi, E. & Sussman, B. Quantum light-field microscopy for volumetric imaging with extreme depth of field. Phys. Rev. Appl. 21, 024029 (2024). This work demonstrates an emerging use of photon-pair correlations for light-field microscopy, taking advantage of advances in time-resolved detection to access both position and momentum information, and achieve volumetric imaging.

    Article  ADS  Google Scholar 

  72. Yan, F. & Venegas-Andraca, S. E. Lessons from twenty years of quantum image processing. ACM Trans. Quantum Comput. 6, 1–29 (2025).

    Article  MathSciNet  Google Scholar 

  73. Marks, R. J. II Handbook of Fourier Analysis & Its Applications (Oxford Univ. Press, 2009).

  74. Zerom, P., Chan, K. W. C., Howell, J. C. & Boyd, R. W. Entangled-photon compressive ghost imaging. Phys. Rev. A 84, 061804 (2011).

    Article  ADS  Google Scholar 

  75. Duarte, M. F. et al. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 25, 83–91 (2008).

    Article  ADS  Google Scholar 

  76. Rodríguez-Fajardo, V., Pinnell, J. & Forbes, A. Towards time-efficient ghost imaging. J. Mod. Opt. 67, 1176–1183 (2020).

    Article  ADS  Google Scholar 

  77. Nothlawala, F., Moodley, C., Gounden, N., Nape, I. & Forbes, A. Quantum ghost imaging by sparse spatial mode reconstruction. Adv. Quantum Technol. 8, 2400577 (2025). This work demonstrates that imaging time can be reduced by orders of magnitude by shifting from the pixel basis to a spatial mode basis, matching object symmetry with basis symmetry.

    Article  Google Scholar 

  78. Ferri, F., Magatti, D., Lugiato, L. & Gatti, A. Differential ghost imaging. Phys. Rev. Lett. 104, 253603 (2010).

    Article  ADS  Google Scholar 

  79. Losero, E. et al. Quantum differential ghost microscopy. Phys. Rev. A 100, 063818 (2019).

    Article  ADS  Google Scholar 

  80. Luo, K.-H., Huang, B.-Q., Zheng, W.-M. & Wu, L.-A. Nonlocal imaging by conditional averaging of random reference measurements. Chin. Phys. Lett. 29, 074216 (2012).

    Article  ADS  Google Scholar 

  81. Liu, H.-C., Yang, H., Xiong, J. & Zhang, S. Positive and negative ghost imaging. Phys. Rev. Appl. 12, 034019 (2019).

    Article  ADS  Google Scholar 

  82. Sun, B., Welsh, S. S., Edgar, M. P., Shapiro, J. H. & Padgett, M. J. Normalized ghost imaging. Opt. Express 20, 16892–16901 (2012).

    Article  ADS  Google Scholar 

  83. Moodley, C. & Forbes, A. Advances in quantum imaging with machine intelligence. Laser Photonics Rev. 18, 2300939 (2024).

    Article  ADS  Google Scholar 

  84. Hinton, G. E. & Salakhutdinov, R. R. Reducing the dimensionality of data with neural networks. Science 313, 504–507 (2006).

    Article  ADS  MathSciNet  Google Scholar 

  85. Lyu, M. et al. Deep-learning-based ghost imaging. Sci. Rep. 7, 17865 (2017).

    Article  ADS  Google Scholar 

  86. Moodley, C., Sephton, B., Rodríguez-Fajardo, V. & Forbes, A. Deep learning early stopping for non-degenerate ghost imaging. Sci. Rep. 11, 8561 (2021).

    Article  ADS  Google Scholar 

  87. Moodley, C. & Forbes, A. Super-resolved quantum ghost imaging. Sci. Rep. 12, 10346 (2022).

    Article  ADS  Google Scholar 

  88. Li, L., Kumar, S., Sua, Y. M. & Huang, Y.-P. Noise-resilient single-pixel compressive sensing with single photon counting. Commun. Phys. 7, 110 (2024).

    Article  Google Scholar 

  89. Wang, Y., Xia, H., Zhou, M., Xie, L. & He, W. A deep learning-based target recognition method for entangled optical quantum imaging system. IEEE Trans. Instrum. Meas. 72, 1–12 (2023).

    Google Scholar 

  90. Defienne, H. et al. Advances in quantum imaging. Nat. Photonics 18, 1024–1036 (2024).

    Article  ADS  Google Scholar 

  91. Gilaberte Basset, M. et al. Perspectives for applications of quantum imaging. Laser Photonics Rev. 13, 1900097 (2019).

    Article  ADS  Google Scholar 

  92. Moreau, P.-A., Toninelli, E., Gregory, T. & Padgett, M. J. Imaging with quantum states of light. Nat. Rev. Phys. 1, 367–380 (2019).

    Article  Google Scholar 

  93. Ryan, D. P. et al. Infrared quantum ghost imaging of living and undisturbed plants. Optica 11, 1261–1267 (2024). This study demonstrates IR quantum ghost imaging of living plants under extremely low illumination, highlighting the potential of quantum imaging for studying light-sensitive biological samples.

    Article  ADS  Google Scholar 

  94. Zhang, Y. et al. Quantum imaging of biological organisms through spatial and polarization entanglement. Sci. Adv. 10, eadk1495 (2024). This work shows quantum imaging of biological organisms using spatial and polarization entanglement, illustrating how multiple degrees of freedom can enhance contrast.

    Article  Google Scholar 

  95. Brida, G. et al. Measurement of sub-shot-noise spatial correlations without background subtraction. Phys. Rev. Lett. 102, 213602 (2009).

    Article  ADS  Google Scholar 

  96. Blanchet, J.-L., Devaux, F., Furfaro, L. & Lantz, E. Measurement of sub-shot-noise correlations of spatial fluctuations in the photon-counting regime. Phys. Rev. Lett. 101, 233604 (2008).

    Article  ADS  Google Scholar 

  97. Nape, I. et al. Measuring dimensionality and purity of high-dimensional entangled states. Nat. Commun. 12, 5159 (2021).

    Article  ADS  Google Scholar 

  98. Mukai, Y., Okamoto, R. & Takeuchi, S. Quantum Fourier-transform infrared spectroscopy in the fingerprint region. Opt. Express 30, 22624–22636 (2022).

    Article  ADS  Google Scholar 

  99. Paterova, A. V., Toa, Z. S., Yang, H. & Krivitsky, L. A. Broadband quantum spectroscopy at the fingerprint mid-infrared region. ACS Photonics 9, 2151–2159 (2022).

    Article  Google Scholar 

  100. Schunemann, P. G., Zawilski, K. T., Pomeranz, L. A., Creeden, D. J. & Budni, P. A. Advances in nonlinear optical crystals for mid-infrared coherent sources. J. Opt. Soc. Am. B 33, D36–D43 (2016).

    Article  Google Scholar 

  101. Schunemann, P. G. New nonlinear crystals for ultrafast frequency conversion in the mid-infrared. In Proc. Ultrafast Optics 2023 — UFOXIII paper Th3.2 (Optica Publishing Group, 2023).

  102. Xiao, Y. & Chen, W. Ghost diffraction in complex scattering media: principles and applications. Appl. Phys. Rev. 12, 021329 (2025).

    Article  ADS  Google Scholar 

  103. Bina, M. et al. Backscattering differential ghost imaging in turbid media. Phys. Rev. Lett. 110, 083901 (2013).

    Article  ADS  Google Scholar 

  104. Dixon, P. B. et al. Quantum ghost imaging through turbulence. Phys. Rev. A 83, 051803 (2011).

    Article  ADS  Google Scholar 

  105. Defienne, H. et al. Pixel super-resolution with spatially entangled photons. Nat. Commun. 13, 3566 (2022).

    Article  ADS  Google Scholar 

  106. Pearce, E. et al. Practical quantum imaging with undetected photons. Opt. Contin. 2, 2386–2397 (2023).

    Article  Google Scholar 

  107. Rizvi, S., Cao, J., Zhang, K. & Hao, Q. Deepghost: real-time computational ghost imaging via deep learning. Sci. Rep. 10, 11400 (2020).

    Article  Google Scholar 

  108. Li, F., Sun, Y. & Zhang, X. Deep-learning-based quantum imaging using NOON states. J. Phys. Commun. 6, 035005 (2022).

    Article  Google Scholar 

  109. Moodley, C., Ruget, A., Leach, J. & Forbes, A. Time-efficient object recognition in quantum ghost imaging. Adv. Quantum Technol. 6, 2200109 (2023).

    Article  Google Scholar 

Download references

Acknowledgements

E.P. acknowledges financial support from the Research Councils UK Engineering and Physical Sciences Research Council-funded Quantum Technology Hub in Sensing, Imaging and Timing (QuSIT) (EP/Z633166/1). F.N. acknowledges funding from the African Laser Centre, Council for Scientific and Industrial Research under the HCD-IBS scholarship scheme. F.N. and A.F. acknowledge funding from the South African Quantum Technology Initiative. M.J.P. acknowledges financial support from the Royal Society (RSRP/R1/211013P).

Author information

Authors and Affiliations

  1. School of Physics and Astronomy, University of Glasgow, Glasgow, UK

    Emma Pearce & Miles J. Padgett

  2. School of Physics, University of the Witwatersrand, Johannesburg, South Africa

    Fazilah Nothlawala & Andrew Forbes

Authors
  1. Emma Pearce
    View author publications

    Search author on:PubMed Google Scholar

  2. Fazilah Nothlawala
    View author publications

    Search author on:PubMed Google Scholar

  3. Andrew Forbes
    View author publications

    Search author on:PubMed Google Scholar

  4. Miles J. Padgett
    View author publications

    Search author on:PubMed Google Scholar

Contributions

All authors contributed to the writing and editing of the manuscript.

Corresponding author

Correspondence to Miles J. Padgett.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Reviews Methods Primers thanks Wen Chen and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Related links

266 nm (quadrupled Nd:YAG): https://www.toptica.com/products/single-frequency-lasers/topwave-duv/topwave-266

355 nm (tripled Nd:YAG): https://www.spectra-physics.com/mam/celum/celum_assets/sp/resources/Vanguard-Datasheet.pdf

405 nm (GaN diodes): https://coherentinc.my.site.com/Coherent/lasers/lasers-laser-systems/obis-lx-ls/1284371?cclcl=en_US

532 nm (doubled Nd:YAG): https://www.oxxius.com/products/lbx-405-3/

β-barium borate (BBO): https://www.thorlabs.com/thorproduct.cfm?partnumber=NLCQ1

Avalanche photodiodes: https://www.excelitas.com/product/spcm-nir

EMCCD cameras: https://andor.oxinst.com/products/emccd-cameras-for-physical-science?_gl=1*jfmife*_up*MQ..*_gs*MQ..&gclid=Cj0KCQjw3OjGBhDYARIsADd-uX5gMn3ug4WcywhlSXjFOTmS-bONUSjocdK8WKKVI0zn406GjK1OZDgaApdWEALw_wcB&gbraid=0AAAAAD_Q0YuL9kNrR6QdpVVWkwz8EkOhT

Intensified CCD: https://andor.oxinst.com/products/intensified-camera-series/

IR avalanche photodiodes: https://marketing.idquantique.com/acton/attachment/11868/f-9ced924d-0c5d-4d2f-ac13-afadb7868ab2/1/-/-/-/-/ID220%20Product%20Brochure.pdf

IR crystals: https://eksmaoptics.com/nonlinear-and-laser-crystals/nonlinear-crystals/infrared-nonlinear-aggas2-aggase2-gase-zngep2-crystals/

Keras: https://keras.io/getting_started/

Modified National Institute of Standards and Technology (MNIST): https://huggingface.co/datasets/ylecun/mnist

PPKTP: https://raicol.com/product/quantum-components/ppktp

PPLN: https://covesion.com/solutions/mgoppln-bulk-crystals/

Scientific CMOS cameras: https://www.hamamatsu.com/jp/en/product/cameras/cmos-cameras.html

Single-photon avalanche diodes (SPADs): https://www.photon-force.com/products/pf32-camera-range/

TensorFlow: https://www.tensorflow.org

Glossary

4f imaging system

A typical imaging telescope consisting of two lenses separated by the sum of their focal lengths.

Bucket detector

A light-collecting detector that counts how much light arrived, thereby integrating out any spatial information.

Einstein–Podolsky–Rosen paradox

Describes how two separated particles can show strong correlations in both position and momentum, without violation of the Heisenberg uncertainty relationship.

Electron-multiplying CCD cameras

(EMCCD cameras). Similar to intensified charge-coupled devices (CCDs), except without the image intensifier; suitable for measuring low photon fluxes.

Far-field plane

The position along the light path where the Fourier transform of an initial complex field is produced, mimicking propagation over long distances (far field), albeit with a scaling difference.

Field of view

The viewing angle or area of the optical system.

Hong–Ou–Mandel dip

Phenomenon in which indistinguishable photons interfere on a beam splitter and so always leave by the same port, causing a dip in coincidence measurements at the outputs.

Idler

The lower-energy (frequency) photon emitted from a nonlinear process.

Image intensifier

A device to amplify the incoming light signal, often by electro-optical means, and used in intensified charge-coupled device cameras.

Image plane

The position along the light path where an initial complex field is reproduced with some magnification.

Non-local

Effects or information shared between spatially separated locations. For example, non-local correlations between measurements in complementary bases are a hallmark of quantum entanglement.

Phase matching

Maintaining a constant or near-constant phase relation between the pump light and the light generated from the nonlinear process (such as between the spontaneous parametric down-conversion pump light and the spontaneous parametric down-conversion photons).

Photon correlations

The joint outcome of both photons when measured in coincidence rather than each being measured independently.

Point detector

A detector that returns the photon counts in a spatially resolved manner.

Relay imaging

The use of lenses to form an intermediate image, allowing image or far-field planes to be re-imaged onto a detector or another part of the system.

Signal

The higher-energy (frequency) photon emitted from a nonlinear process.

Spatial coherence

The correlations in phase across space, such as the separation in the transverse plane, where waves can still interfere with each other.

Spoof-resistant signalling

Signalling that is able to avoid fake data or parties passing for the real thing.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pearce, E., Nothlawala, F., Forbes, A. et al. Quantum imaging with correlated photon pairs. Nat Rev Methods Primers 6, 17 (2026). https://doi.org/10.1038/s43586-025-00468-x

Download citation

  • Accepted:

  • Published:

  • Version of record:

  • DOI: https://doi.org/10.1038/s43586-025-00468-x

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing