Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Perspective
  • Published:

Computational design of mechanical metamaterials

Nature Computational Science volume 4, pages 574–583 (2024)Cite this article

Subjects

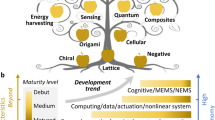
Abstract

In the past few years, design of mechanical metamaterials has been empowered by computational tools that have allowed the community to overcome limitations of human intuition. By leveraging efficient optimization algorithms and computational physics models, it is now possible to explore vast design spaces, achieving new material functionalities with unprecedented performance. Here, we present our viewpoint on the state of the art of computational metamaterials design, discussing recent advances in topology optimization and machine learning design with respect to challenges in additive manufacturing.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Metamaterials generated by continuous optimization.
Fig. 2: Flexible metamaterials obtained through discrete optimization.
Fig. 3: Example of using ML for the design of MM for different purposes.

Similar content being viewed by others

References

  1. Bertoldi, K., Vitelli, V., Christensen, J. & Van Hecke, M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2, 17066 (2017).

    Article  Google Scholar 

  2. Xia, X., Spadaccini, C. M. & Greer, J. R. Responsive materials architected in space and time. Nat. Rev. Mater. 7, 683–701 (2022).

    Article  Google Scholar 

  3. Lakes, R. Foam structures with a negative poisson’s ratio. Science 235, 1038–1040 (1987).

    Article  Google Scholar 

  4. Lakes, R. Deformation mechanisms in negative poisson’s ratio materials: structural aspects. J. Mater. Sci. 26, 2287–2292 (1991).

    Article  Google Scholar 

  5. Milton, G. W. Composite materials with poisson’s ratios close to – 1. J. Mech. Phys. Solids 40, 1105–1137 (1992).

    Article  MathSciNet  Google Scholar 

  6. Sigmund, O. Materials with prescribed constitutive parameters: an inverse homogenization problem. Int. J. Solids Struct. 31, 2313–2329 (1994).

    Article  MathSciNet  Google Scholar 

  7. Sigmund, O. Tailoring materials with prescribed elastic properties. Mech. Mater. 20, 351–368 (1995).

    Article  Google Scholar 

  8. Evans, K. E. & Alderson, A. Auxetic materials: functional materials and structures from lateral thinking! Adv. Mater. 12, 617–628 (2000).

    Article  Google Scholar 

  9. Coulais, C., Kettenis, C. & van Hecke, M. A characteristic length scale causes anomalous size effects and boundary programmability in mechanical metamaterials. Nat. Phys. 14, 40–44 (2017).

    Article  Google Scholar 

  10. Florijn, B., Coulais, C. & van Hecke, M. Programmable mechanical metamaterials. Phys. Rev. Lett. 113, 175503 (2014).

    Article  Google Scholar 

  11. Florijn, B., Coulais, C. & van Hecke, M. Programmable mechanical metamaterials: the role of geometry. Soft Matter 12, 8736–8743 (2016).

    Article  Google Scholar 

  12. Rayneau-Kirkhope, D. J. & Dias, M. A. Recipes for selecting failure modes in 2-d lattices. Extreme Mech. Lett. 9, 11–20 (2016).

    Article  Google Scholar 

  13. Gibson, L. J., Ashby, M. F. & Harley, B. A. Cellular Materials in Nature and Medicine (Cambridge Univ. Press, 2010).

  14. Ashby, M. F. The properties of foams and lattices. Philos. Trans. R. Soc. A 364, 15–30 (2006).

    Article  MathSciNet  Google Scholar 

  15. Rayneau-Kirkhope, D., Bonfanti, S. & Zapperi, S. Density scaling in the mechanics of a disordered mechanical meta-material. Appl. Phys. Lett. 114, 111902 (2019).

  16. Lin, X. et al. Mechanical fourier transform for programmable metamaterials. Proc. Natl Acad. Sci. USA 120, e2305380120 (2023).

    Article  Google Scholar 

  17. Frenzel, T., Kadic, M. & Wegener, M. Three-dimensional mechanical metamaterials with a twist. Science 358, 1072–1074 (2017).

    Article  Google Scholar 

  18. Fernandez-Corbaton, I. et al. New twists of 3D chiral metamaterials. Adv. Mater. 31, 1807742 (2019).

    Article  Google Scholar 

  19. Wu, W. et al. Mechanical design and multifunctional applications of chiral mechanical metamaterials: a review. Mater. Des. 180, 107950 (2019).

    Article  Google Scholar 

  20. Bertoldi, K., Reis, P. M., Willshaw, S. & Mullin, T. Negative Poisson’s ratio behavior induced by an elastic instability. Adv. Mater. 22, 361–366 (2010).

    Article  Google Scholar 

  21. Zhang, H., Wu, J., Fang, D. & Zhang, Y. Hierarchical mechanical metamaterials built with scalable tristable elements for ternary logic operation and amplitude modulation. Sci. Adv. 7, eabf1966 (2021).

    Article  Google Scholar 

  22. Zhang, X. et al. Kirigami-based metastructures with programmable multistability. Proc. Natl Acad. Sci. USA 119, e2117649119 (2022).

    Article  MathSciNet  Google Scholar 

  23. Bendsoe, M. P. & Sigmund, O.Topology Optimization: Theory, Methods, and Applications (Springer Science and Business Media, 2003).

  24. Sigmund, O. & Maute, K. Topology optimization approaches: a comparative review. Struct. Multidiscip. Optim. 48, 1031–1055 (2013).

    Article  MathSciNet  Google Scholar 

  25. Bendsøe, M. P. Optimal shape design as a material distribution problem. Struct. Optim. 1, 193–202 (1989).

    Article  Google Scholar 

  26. Zhou, M. & Rozvany, G. The COC algorithm, Part II: topological, geometrical and generalized shape optimization. Comput. Methods Appl. Mech. Eng. 89, 309–336 (1991).

    Article  Google Scholar 

  27. Mlejnek, H.-P. & Schirrmacher, R. An engineer’s approach to optimal material distribution and shape finding. Comput. Methods Appl. Mech. Eng. 106, 1–26 (1993).

    Article  Google Scholar 

  28. Diaz, A. & Sigmund, O. Checkerboard patterns in layout optimization. Struct. Optim. 10, 40–45 (1995).

    Article  Google Scholar 

  29. Jog, C. S. & Haber, R. B. Stability of finite element models for distributed-parameter optimization and topology design. Comput. Methods Appl. Mech. Eng. 130, 203–226 (1996).

    Article  MathSciNet  Google Scholar 

  30. Sigmund, O. & Petersson, J. Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct. Optim. 16, 68–75 (1998).

    Article  Google Scholar 

  31. Sigmund, O. On the design of compliant mechanisms using topology optimization. J. Struct. Mech. 25, 493–524 (1997).

    Google Scholar 

  32. Bourdin, B. Filters in topology optimization. Int. J. Numer. Methods Eng. 50, 2143–2158 (2001).

    Article  MathSciNet  Google Scholar 

  33. Bruns, T. E. & Tortorelli, D. A. Topology optimization of non-linear elastic structures and compliant mechanisms. Comput. Methods Appl. Mech. Eng. 190, 3443–3459 (2001).

    Article  Google Scholar 

  34. Lazarov, B. S. & Sigmund, O. Filters in topology optimization based on Helmholtz-type differential equations. Int. J. Numer. Methods Eng. 86, 765–781 (2011).

    Article  MathSciNet  Google Scholar 

  35. Prager, W. & Taylor, J. E. Problems of optimal structural design. J. Appl. Mech. 35, 102–106 (1968).

  36. Svanberg, K. The method of moving asymptotes-a new method for structural optimization. Int. J. Numer. Methods Eng. 24, 359–373 (1987).

    Article  MathSciNet  Google Scholar 

  37. Bourdin, B. & Chambolle, A. Design-dependent loads in topology optimization. ESAIM Control. Optim. Calc. Var. 9, 19–48 (2003).

    Article  MathSciNet  Google Scholar 

  38. Wang, M. Y. & Zhou, S. Phase field: a variational method for structural topology optimization. Comput. Model. Eng. Sci. 6, 547–566 (2004).

    MathSciNet  Google Scholar 

  39. Garcke, H., Lam, K. F., Nürnberg, R. & Signori, A. Overhang penalization in additive manufacturing via phase field structural topology optimization with anisotropic energies. Appl. Math. Optim. 87, 44 (2023).

    Article  MathSciNet  Google Scholar 

  40. Osher, S. & Sethian, J. A. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 79, 12–49 (1988).

    Article  MathSciNet  Google Scholar 

  41. Sethian, J. A. & Wiegmann, A. Structural boundary design via level set and immersed interface methods. J. Comput. Phys. 163, 489–528 (2000).

    Article  MathSciNet  Google Scholar 

  42. Allaire, G., Gournay, F. D., Jouve, F. & Toader, A.-M. Structural optimization using topological and shape sensitivity via a level set method. Control Cybern. 34, 59–80 (2005).

    MathSciNet  Google Scholar 

  43. Van Dijk, N. P., Maute, K., Langelaar, M. & Van Keulen, F. Level-set methods for structural topology optimization: a review. Struct. Multidiscip. Optim. 48, 437–472 (2013).

    Article  MathSciNet  Google Scholar 

  44. Shim, P. Y. & Manoochehri, S. Generating optimal configurations in structural design using simulated annealing. Int. J. Numer. Methods Eng. 40, 1053–1069 (1997).

    Article  Google Scholar 

  45. Bonfanti, S., Guerra, R., Font-Clos, F., Rayneau-Kirkhope, D. & Zapperi, S. Automatic design of mechanical metamaterial actuators. Nat. Commun. 11, 4162 (2020).

    Article  Google Scholar 

  46. Beretta, L. et al. Automatic design of chiral mechanical metamaterials. APL Mater. 9, 101112 (2021).

    Article  Google Scholar 

  47. Wu, C.-Y. & Tseng, K.-Y. Topology optimization of structures using modified binary differential evolution. Struct. Multidiscip. Optim. 42, 939–953 (2010).

    Article  Google Scholar 

  48. Kitayama, S., Arakawa, M. & Yamazaki, K. Differential evolution as the global optimization technique and its application to structural optimization. Appl. Soft Comput. 11, 3792–3803 (2011).

    Article  Google Scholar 

  49. Madeira, J. A., Pina, H. & Rodrigues, H. GA topology optimization using random keys for tree encoding of structures. Struct. Multidiscip. Optim. 40, 227–240 (2010).

    Article  Google Scholar 

  50. Zhang, J. & Yanagimoto, J. Density-based topology optimization integrated with genetic algorithm for optimizing formability and bending stiffness of 3d printed cfrp core sandwich sheets. Compos. Part B 225, 109248 (2021).

    Article  Google Scholar 

  51. Mattheck, C. & Burkhardt, S. A new method of structural shape optimization based on biological growth. Int. J. Fatigue 12, 185–190 (1990).

    Article  Google Scholar 

  52. Xie, Y. M. & Steven, G. P. A simple evolutionary procedure for structural optimization. Comput. Struct. 49, 885–896 (1993).

    Article  Google Scholar 

  53. Querin, O. M., Steven, G. P. & Xie, Y. M. Evolutionary structural optimisation (ESO) using a bidirectional algorithm. Eng. Comput. 15, 1031–1048 (1998).

    Article  Google Scholar 

  54. Young, V., Querin, O. M., Steven, G. & Xie, Y. 3D and multiple load case bi-directional evolutionary structural optimization (BESO). Struct. Optim. 18, 183–192 (1999).

    Article  Google Scholar 

  55. Sigmund, O. On the usefulness of non-gradient approaches in topology optimization. Struct. Multidiscip. Optim. 43, 589–596 (2011).

    Article  MathSciNet  Google Scholar 

  56. Zhang, S. & Norato, J. A. Finding better local optima in topology optimization via tunneling. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference Vol. 51760, V02BT03A014 (American Society of Mechanical Engineers, 2018).

  57. Martinez, P., Marti, P. & Querin, O. Growth method for size, topology, and geometry optimization of truss structures. Struct. Multidiscip. Optim. 33, 13–26 (2007).

    Article  Google Scholar 

  58. Zhu, B. et al. Design of compliant mechanisms using continuum topology optimization: a review. Mech. Mach. Theory 143, 103622 (2020).

    Article  Google Scholar 

  59. Yoon, G., Kim, Y., Bendsøe, M. P. & Sigmund, O. Hinge-free topology optimization with embedded translation-invariant differentiable wavelet shrinkage. Struct. Multidiscip. Optim. 27, 139–150 (2004).

    Article  Google Scholar 

  60. Luo, Z., Chen, L., Yang, J., Zhang, Y. & Abdel-Malek, K. Compliant mechanism design using multi-objective topology optimization scheme of continuum structures. Struct. Multidiscip. Optim. 30, 142–154 (2005).

    Article  Google Scholar 

  61. Poulsen, T. A. A simple scheme to prevent checkerboard patterns and one-node connected hinges in topology optimization. Struct. Multidiscip. Optim. 24, 396–399 (2002).

    Article  Google Scholar 

  62. Zhang, W., Zhong, W. & Guo, X. An explicit length scale control approach in simp-based topology optimization. Comput. Methods Appl. Mech. Eng. 282, 71–86 (2014).

    Article  MathSciNet  Google Scholar 

  63. Poulsen, T. A. A new scheme for imposing a minimum length scale in topology optimization. Int. J. Numer. Methods Eng. 57, 741–760 (2003).

    Article  MathSciNet  Google Scholar 

  64. Seltmann, S. & Hasse, A. Topology optimization of compliant mechanisms with distributed compliance (hinge-free compliant mechanisms) by using stiffness and adaptive volume constraints instead of stress constraints. Mech. Mach. Theory 180, 105133 (2023).

    Article  Google Scholar 

  65. de Assis Pereira, A. & Cardoso, E. L. On the influence of local and global stress constraint and filtering radius on the design of hinge-free compliant mechanisms. Struct. Multidiscip. Optim. 58, 641–655 (2018).

    Article  Google Scholar 

  66. Jonsmann, J., Sigmund, O. & Bouwstra, S. Compliant thermal microactuators. Sens. Actuators A 76, 463–469 (1999).

    Article  Google Scholar 

  67. Jonsmann, J., Sigmund, O. & Bouwstra, S. Compliant electro-thermal microactuators. In Technical Digest. IEEE International MEMS 99 Conference. Twelfth IEEE International Conference on Micro Electro Mechanical Systems 588–593 (IEEE, 1999).

  68. Sigmund, O. Design of multiphysics actuators using topology optimization – Part I: one-material structures. Comput. Methods Appl. Mech. Eng. 190, 6577–6604 (2001).

    Article  Google Scholar 

  69. Sigmund, O. Design of multiphysics actuators using topology optimization – Part II: two-material structures. Comput. Methods Appl. Mech. Eng. 190, 6605–6627 (2001).

    Article  Google Scholar 

  70. Bruns, T. & Sigmund, O. Toward the topology design of mechanisms that exhibit snap-through behavior. Comput. Methods Appl. Mech. Eng. 193, 3973–4000 (2004).

    Article  MathSciNet  Google Scholar 

  71. Prasad, J. & Diaz, A. Synthesis of bistable periodic structures using topology optimization and a genetic algorithm. J. Mech. Des. 128, 1298–1306 (2006).

  72. Ohsaki, M. et al. Enumeration of optimal pin-jointed bistable compliant mechanisms with non-crossing members. Struct. Multidiscip. Optim. 37, 645–651 (2009).

    Article  Google Scholar 

  73. Zhang, D., Zhai, X., Liu, L. & Fu, X.-M. An optimized, easy-to-use, open-source gpu solver for large-scale inverse homogenization problems. Struct. Multidiscip. Optim. 66, 207 (2023).

    Article  MathSciNet  Google Scholar 

  74. Laman, G. On graphs and rigidity of plane skeletal structures. J. Eng. Math. 4, 331–340 (1970).

    Article  MathSciNet  Google Scholar 

  75. Roth, B. Rigid and flexible frameworks. Am. Math. Monthly 88, 6–21 (1981).

    Article  MathSciNet  Google Scholar 

  76. Borcea, C. S. & Streinu, I. Periodic frameworks and flexibility. Proc. R. Soc. A 466, 2633–2649 (2010).

    Article  MathSciNet  Google Scholar 

  77. Mitschke, H. et al. Finding auxetic frameworks in periodic tessellations. Adv. Mater. 23, 2669–2674 (2011).

    Article  Google Scholar 

  78. Wang, F. & Sigmund, O. 3D architected isotropic materials with tunable stiffness and buckling strength. J. Mech. Phys. Solids 152, 104415 (2021).

    Article  MathSciNet  Google Scholar 

  79. Wang, F., Brøns, M. & Sigmund, O. Non-hierarchical architected materials with extreme stiffness and strength. Adv. Funct. Mater. 33, 2211561 (2023).

    Article  Google Scholar 

  80. Clausen, A., Wang, F., Jensen, J. S., Sigmund, O. & Lewis, J. A. Topology optimized architectures with programmable poisson’s ratio over large deformations. Adv. Mater. 27, 5523–5527 (2015).

    Article  Google Scholar 

  81. Rodrigues, H., Guedes, J. M. & Bendsoe, M. P. Hierarchical optimization of material and structure. Struct. Multidiscip. Optim. 24, 1–10 (2002).

    Article  Google Scholar 

  82. Coelho, P. G., Fernandes, P. R., Guedes, J. M. & Rodrigues, H. C. A hierarchical model for concurrent material and topology optimisation of three-dimensional structures. Struct. Multidiscip. Optim. 35, 107–115 (2008).

    Article  Google Scholar 

  83. Bendsøe, M. P. & Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 71, 197–224 (1988).

    Article  MathSciNet  Google Scholar 

  84. Avellaneda, M. Optimal bounds and microgeometries for elastic two-phase composites. SIAM J. Appl. Math. 47, 1216–1228 (1987).

    Article  MathSciNet  Google Scholar 

  85. Francfort, G. A. & Murat, F. Homogenization and optimal bounds in linear elasticity. Arch. Ration. Mech. Anal. 94, 307–334 (1986).

    Article  MathSciNet  Google Scholar 

  86. Pantz, O. & Trabelsi, K. A post-treatment of the homogenization method for shape optimization. SIAM J. Control Optim. 47, 1380–1398 (2008).

    Article  MathSciNet  Google Scholar 

  87. Pantz, O. & Trabelsi, K. Construction of minimization sequences for shape optimization. In 2010 15th International Conference on Methods and Models in Automation and Robotics 278–283 (IEEE, 2010).

  88. Allaire, G., Geoffroy-Donders, P. & Pantz, O. Topology optimization of modulated and oriented periodic microstructures by the homogenization method. Comput. Math. Appl. 78, 2197–2229 (2019).

    Article  MathSciNet  Google Scholar 

  89. Geoffroy-Donders, P., Allaire, G. & Pantz, O. 3-d topology optimization of modulated and oriented periodic microstructures by the homogenization method. J. Comput. Phys. 401, 108994 (2020).

    Article  MathSciNet  Google Scholar 

  90. Groen, J. P. & Sigmund, O. Homogenization-based topology optimization for high-resolution manufacturable microstructures. Int. J. Numer. Methods Eng. 113, 1148–1163 (2018).

    Article  MathSciNet  Google Scholar 

  91. Groen, J. P., Stutz, F. C., Aage, N., Bærentzen, J. A. & Sigmund, O. De-homogenization of optimal multi-scale 3D topologies. Comput. Methods Appl. Mech. Eng. 364, 112979 (2020).

    Article  MathSciNet  Google Scholar 

  92. Woldseth, R. V., Bærentzen, J. A. & Sigmund, O. Phasor noise for dehomogenisation in 2D multiscale topology optimisation. Comput. Methods Appl. Mech. Eng. 418, 116551 (2024).

    Article  MathSciNet  Google Scholar 

  93. Jensen, P. D. L., Sigmund, O. & Groen, J. P. De-homogenization of optimal 2D topologies for multiple loading cases. Comput. Methods Appl. Mech. Eng. 399, 115426 (2022).

    Article  MathSciNet  Google Scholar 

  94. Träff, E., Sigmund, O. & Groen, J. Simple single-scale microstructures based on optimal rank-3 laminates. Struct. Multidiscip. Optim. 59, 1021–1031 (2019).

    Article  Google Scholar 

  95. Lazarov, B. S., Wang, F. & Sigmund, O. Length scale and manufacturability in density-based topology optimization. Arch. Appl. Mech. 86, 189–218 (2016).

    Article  Google Scholar 

  96. Qian, X. Undercut and overhang angle control in topology optimization: a density gradient based integral approach. Int. J. Numer. Methods Eng. 111, 247–272 (2017).

    Article  MathSciNet  Google Scholar 

  97. Zhang, K., Cheng, G. & Xu, L. Topology optimization considering overhang constraint in additive manufacturing. Comput. Struct. 212, 86–100 (2019).

    Article  Google Scholar 

  98. Gaynor, A. T. & Guest, J. K. Topology optimization considering overhang constraints: eliminating sacrificial support material in additive manufacturing through design. Struct. Multidiscip. Optim. 54, 1157–1172 (2016).

    Article  MathSciNet  Google Scholar 

  99. Langelaar, M. Topology optimization for additive manufacturing with controllable support structure costs. In 7th European Congress on Computational Methods in Applied Sciences and Engineering 3689–3699 (National Technical University of Athens, 2016).

  100. Langelaar, M. An additive manufacturing filter for topology optimization of print-ready designs. Struct. Multidiscip. Optim. 55, 871–883 (2017).

    Article  Google Scholar 

  101. Luo, Y., Sigmund, O., Li, Q. & Liu, S. Additive manufacturing oriented topology optimization of structures with self-supported enclosed voids. Comput. Methods Appl. Mech. Eng. 372, 113385 (2020).

    Article  MathSciNet  Google Scholar 

  102. Sabiston, G. & Kim, I. Y. Void region restriction for additive manufacturing via a diffusion physics approach. Int. J. Numer. Methods Eng. 121, 4347–4373 (2020).

    Article  MathSciNet  Google Scholar 

  103. Donoso, A., Aranda, E. & Ruiz, D. A new approach based on spectral graph theory to avoiding enclosed holes in topology optimization. Comput. Methods Appl. Mech. Eng. 393, 114769 (2022).

    Article  MathSciNet  Google Scholar 

  104. Gaynor, A. T. & Johnson, T. E. Eliminating occluded voids in additive manufacturing design via a projection-based topology optimization scheme. Addit. Manuf. 33, 101149 (2020).

    Google Scholar 

  105. Xiong, Y., Yao, S., Zhao, Z.-L. & Xie, Y. M. A new approach to eliminating enclosed voids in topology optimization for additive manufacturing. Addit. Manuf. 32, 101006 (2020).

    Google Scholar 

  106. Wang, C. Simultaneous optimization of build orientation and topology for self-supported enclosed voids in additive manufacturing. Comput. Methods Appl. Mech. Eng. 388, 114227 (2022).

    Article  MathSciNet  Google Scholar 

  107. Bruggi, M., Laghi, V. & Trombetti, T. Simultaneous design of the topology and the build orientation of wire-and-arc additively manufactured structural elements. Comput. Struct. 242, 106370 (2021).

    Article  Google Scholar 

  108. Mishra, V., Ayas, C., Langelaar, M. & Van Keulen, F. Simultaneous topology and deposition direction optimization for wire and arc additive manufacturing. Manuf. Lett. 31, 45–51 (2022).

    Article  Google Scholar 

  109. Michaleris, P. Modeling metal deposition in heat transfer analyses of additive manufacturing processes. Finite Elem. Anal. Des. 86, 51–60 (2014).

    Article  Google Scholar 

  110. Ranjan, R., Ayas, C., Langelaar, M. & van Keulen, F. Fast detection of heat accumulation in powder bed fusion using computationally efficient thermal models. Materials 13, 4576 (2020).

    Article  Google Scholar 

  111. Ranjan, R., Ayas, C., Langelaar, M. & Keulen, F. V. Controlling local overheating in topology optimization for additive manufacturing. Struct. Multidiscip. Optim. 65, 162 (2022).

    Article  Google Scholar 

  112. Ueda, Y., Fukuda, K., Nakacho, K. & Endo, S. A new measuring method of residual stresses with the aid of finite element method and reliability of estimated values. J. Soc. Nav. Archit. Jpn 1975, 499–507 (1975).

    Article  Google Scholar 

  113. Liang, X., Cheng, L., Chen, Q., Yang, Q. & To, A. C. A modified method for estimating inherent strains from detailed process simulation for fast residual distortion prediction of single-walled structures fabricated by directed energy deposition. Addit. Manuf. 23, 471–486 (2018).

    Google Scholar 

  114. Bihr, M. et al. Part and supports optimization in metal powder bed additive manufacturing using simplified process simulation. Comput. Methods Appl. Mech. Eng. 395, 114975 (2022).

    Article  MathSciNet  Google Scholar 

  115. Mishra, V., Ayas, C., Langelaar, M. & van Keulen, F. On controlling microstructure through topology optimization for additive manufacturing. In Proceedings of the ASMO UK12-EU1 Conference Engineering Design Optimization 147 (2022).

  116. Bayat, M. et al. Holistic computational design within additive manufacturing through topology optimization combined with multiphysics multi-scale materials and process modelling. Prog. Mater. Sci. 138, 101129 (2023).

  117. Shi, R. et al. Microstructural control in metal laser powder bed fusion additive manufacturing using laser beam shaping strategy. Acta Mater. 184, 284–305 (2020).

    Article  Google Scholar 

  118. Saghaian, S. E. et al. Effect of hatch spacing and laser power on microstructure, texture, and thermomechanical properties of laser powder bed fusion (L-PBF) additively manufactured NiTi. Opt. Laser Technol. 149, 107680 (2022).

    Article  Google Scholar 

  119. Fu, Z., Ye, J., Franke, M. & Körner, C. A novel approach for powder bed-based additive manufacturing of compositionally graded composites. Addit. Manuf. 56, 102916 (2022).

    Google Scholar 

  120. Liu, Z. et al. Additive manufacturing of metals: microstructure evolution and multistage control. J. Mater. Sci. Technol. 100, 224–236 (2022).

    Article  Google Scholar 

  121. Woldseth, R. V., Aage, N., Bærentzen, J. A. & Sigmund, O. On the use of artificial neural networks in topology optimisation. Struct. Multidiscip. Optim. 65, 294 (2022).

    Article  Google Scholar 

  122. Shin, S., Shin, D. & Kang, N. Topology optimization via machine learning and deep learning: A review. J. Comput. Des. Eng. 10, 1736–1766 (2023).

    Google Scholar 

  123. Zheng, X., Zhang, X., Chen, T.-T. & Watanabe, I. Deep learning in mechanical metamaterials: from prediction and generation to inverse design. Adv. Mater. 35, 2302530 (2023).

  124. Jiao, P., Mueller, J., Raney, J. R., Zheng, X. & Alavi, A. H. Mechanical metamaterials and beyond. Nat. Commun. 14, 6004 (2023).

    Article  Google Scholar 

  125. Mao, Y., He, Q. & Zhao, X. Designing complex architectured materials with generative adversarial networks. Sci. Adv. 6, eaaz4169 (2020).

    Article  Google Scholar 

  126. Andreassen, E., Clausen, A., Schevenels, M., Lazarov, B. S. & Sigmund, O. Efficient topology optimization in matlab using 88 lines of code. Struct. Multidiscip. Optim. 43, 1–16 (2011).

    Article  Google Scholar 

  127. Kollmann, H. T., Abueidda, D. W., Koric, S., Guleryuz, E. & Sobh, N. A. Deep learning for topology optimization of 2D metamaterials. Mater. Des. 196, 109098 (2020).

    Article  Google Scholar 

  128. Sosnovik, I. & Oseledets, I. Neural networks for topology optimization. Russ. J. Numer. Anal. Math. Model. 34, 215–223 (2019).

    Article  MathSciNet  Google Scholar 

  129. Joo, Y., Yu, Y. & Jang, I. G. Unit module-based convergence acceleration for topology optimization using the spatiotemporal deep neural network. IEEE Access 9, 149766–149779 (2021).

    Article  Google Scholar 

  130. Kallioras, N. A., Kazakis, G. & Lagaros, N. D. Accelerated topology optimization by means of deep learning. Struct. Multidiscip. Optim. 62, 1185–1212 (2020).

    Article  MathSciNet  Google Scholar 

  131. Deng, B. et al. Inverse design of mechanical metamaterials with target nonlinear response via a neural accelerated evolution strategy. Adv. Mater. 34, 2206238 (2022).

    Article  Google Scholar 

  132. Ha, C. S. et al. Rapid inverse design of metamaterials based on prescribed mechanical behavior through machine learning. Nat. Commun. 14, 5765 (2023).

    Article  Google Scholar 

  133. Greminger, M. Generative adversarial networks with synthetic training data for enforcing manufacturing constraints on topology optimization. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference Vol. 84003, V11AT11A005 (American Society of Mechanical Engineers, 2020).

  134. Oh, S., Jung, Y., Lee, I. & Kang, N. Design automation by integrating generative adversarial networks and topology optimization. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference Vol. 51753, V02AT03A008 (American Society of Mechanical Engineers, 2018).

  135. Zheng, L., Karapiperis, K., Kumar, S. & Kochmann, D. M. Unifying the design space and optimizing linear and nonlinear truss metamaterials by generative modeling. Nat. Commun. 14, 7563 (2023).

    Article  Google Scholar 

  136. Wang, C., Yao, S., Wang, Z. & Hu, J. Deep super-resolution neural network for structural topology optimization. Eng. Optim. 53, 2108–2121 (2021).

    Article  Google Scholar 

  137. Napier, N., Sriraman, S.-A., Tran, H. T. & James, K. A. An artificial neural network approach for generating high-resolution designs from low-resolution input in topology optimization. J. Mech. Des. 142, 011402 (2020).

    Article  Google Scholar 

  138. Elingaard, M. O., Aage, N., Bærentzen, J. A. & Sigmund, O. De-homogenization using convolutional neural networks. Comput. Methods Appl. Mech. Eng. 388, 114197 (2022).

    Article  MathSciNet  Google Scholar 

  139. Hu, Y. Recent progress in field-assisted additive manufacturing: materials, methodologies, and applications. Mater. Horiz. 8, 885–911 (2021).

    Article  Google Scholar 

  140. Lee, R. H., Mulder, E. A. & Hopkins, J. B. Mechanical neural networks: architected materials that learn behaviors. Sci. Robot. 7, eabq7278 (2022).

    Article  Google Scholar 

  141. Dillavou, S. et al. Machine learning without a processor: emergent learning in a nonlinear electronic metamaterial. Proc. Natl Acad. Sci. USA 121, e2319718121 (2023).

  142. Scheidgen, M. et al. NOMAD: a distributed web-based platform for managing materials science research data. J. Open Source Softw. 8, 5388 (2023).

    Article  Google Scholar 

  143. Wilkinson, M. D. et al. The fair guiding principles for scientific data management and stewardship. Sci. Data 3, 160018 (2016).

    Article  Google Scholar 

Download references

Acknowledgements

S.H. acknowledges support from the FRASCAL graduate school (German Research Foundation (DFG); 377472739/GRK 2423/2-2023) and the DFG (grant Za 171 14/1) during the early stages of the work. S.H. also acknowledges support from the Humboldt Foundation through the Feodor Lynen fellowship during the later stages of the work. S.B. was partially supported by the European Union Horizon 2020 research and innovation programme under (grant 857470) and from the European Regional Development Fund under the programme of the Foundation for Polish Science International Research Agenda PLUS (grant MAB PLUS/2018/8). R.G. was supported by the PRIN 2022 project TRIEL. S.Z. was supported by the PRIN 2022 project METACTOR. M.Z. and S.Z. also acknowledge support from DFG (Za 171 9/3). R.Z. was supported by the Italian Ministry of Education Universities and Research through PON Ricerca e Innovazione 2014–2020 (DM 1061, 10 August 2021).

Author information

Authors and Affiliations

  1. Center for Complexity and Biosystems, Department of Physics ‘Aldo Pontremoli’, University of Milan, Milano, Italy

    Silvia Bonfanti, Stefan Hiemer, Raja Zulkarnain, Roberto Guerra & Stefano Zapperi

  2. NOMATEN Centre of Excellence, National Center for Nuclear Research, Swierk/Otwock, Poland

    Silvia Bonfanti

  3. Institute of Materials Simulation, Department of Materials Science Science and Engineering, Friedrich-Alexander-University Erlangen-Nuremberg, Fürth, Germany

    Stefan Hiemer & Michael Zaiser

  4. Consiglio Nazionale delle Ricerche, Istituto di Chimica della Materia Condensata e di Tecnologie per l’Energia, Milano, Italy

    Stefan Hiemer & Stefano Zapperi

Authors
  1. Silvia Bonfanti
    View author publications

    Search author on:PubMed Google Scholar

  2. Stefan Hiemer
    View author publications

    Search author on:PubMed Google Scholar

  3. Raja Zulkarnain
    View author publications

    Search author on:PubMed Google Scholar

  4. Roberto Guerra
    View author publications

    Search author on:PubMed Google Scholar

  5. Michael Zaiser
    View author publications

    Search author on:PubMed Google Scholar

  6. Stefano Zapperi
    View author publications

    Search author on:PubMed Google Scholar

Contributions

S.B., S.H., R.Z., R.G., M.Z. and S.Z. performed the literature review, assembled the figures and wrote the paper.

Corresponding authors

Correspondence to Michael Zaiser or Stefano Zapperi.

Ethics declarations

Competing interests

S.B., R.G. and S.Z. have filed a patent application through the University of Milan related to the present work (application number: 102019000021618). The patent concerns a design method for mechanical actuators. All other authors declare no competing interests.

Peer review

Peer review information

Nature Computational Science thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Fernando Chirigati, in collaboration with the Nature Computational Science team.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bonfanti, S., Hiemer, S., Zulkarnain, R. et al. Computational design of mechanical metamaterials. Nat Comput Sci 4, 574–583 (2024). https://doi.org/10.1038/s43588-024-00672-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s43588-024-00672-x

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing