Introduction

Two-dimensional electrophoresis (2-DE) is a powerful technique for separating complex mixtures of denatured proteins according to two independent criteria: charge and molecular weight (O'Farrell, 1975). Combined with nonspecific protein staining, the technique permits the visualization on a single gel of a very large number of gene products that represent the more abundant proteins in a cell or tissue. Unlike one-dimensional electrophoresis (1-DE), which is restricted to the analysis of native soluble proteins, mainly enzymes, 2-DE allows the examination of a broad spectrum of proteins and, consequently, a substantially increased number of protein-encoding loci. This suggests that 2-DE could have a great potential for the study of genetic variability of populations, in that it allows a more representative sample of the genome to be analysed. However, studies of genetic variability in natural populations of animal species by means of 2-DE have been relatively scarce, because 2-DE is technically more difficult and time consuming than 1-DE and, furthermore, because the first results revealed substantially less genetic variation than had been estimated by 1-DE (Edwards and Hopkinson, 1980; Aquadro and Avise, 1981; Neel, 1990). Moreover, most studies have been focused on a few species (particularly man and Drosophila) so that the available information is to a large extent redundant and biased as a means of getting an appropriate view of the levels of genetic variability detected by 2-DE. In man, 2-DE estimates of average heterozygosity (H) range from 0.000 to 0.040 for different tissues when more than 30 loci are scored (Walton et al, 1979; Smith et al, 1980; Hamaguchi et al, 1981; Comings, 1982; Goldman and Merril, 1983; Rosenblum et al, 1983; Hanash et al, 1986a,1986b; Takahashi et al, 1986). Other studies in man yield higher values of heterozygosity (0.045–0.080) but they are based on less than 30 loci (Rosenblum et al, 1984; Asakawa et al, 1985). Apart from man, only two other species of mammals have been studied by 2-DE with respect to genetic variability: cheetah (H=0.013, O'Brien et al, 1983) and mouse (H=0.020, Racine and Langley, 1980). In invertebrates, 2-DE estimates of genetic variability are restricted to two Drosophila species, in which estimated heterozygosities are rather similar to those reported for mammals (0.040 and 0.018 for whole body and male reproductive tract, respectively, in D. melanogaster and 0.000 and 0.028 for whole body and male reproductive tract, respectively, in D. simulans) (Leigh Brown and Langley, 1979; Ohnishi et al, 1982; Coulthart and Singh, 1988). Therefore, additional estimates of genetic variability by 2-DE for different species of vertebrates and invertebrates are needed. In this article, we have applied 2-DE to determine the level of genetic variation for the most abundant proteins of the marine mussel Mytilus galloprovincialis, remembering that molluscs are one of the taxonomic groups within the animal kingdom where the highest levels of genetic variability have been reported (the mean value of allozyme heterozygosity is 0.145±0.010 for 105 molluscan species reviewed by Ward et al, 1992). In fact, M. galloprovincialis is a mollusc species where a particularly high value of heterozygosity for enzyme loci has been found (H=0.240, Grant and Cherry, 1985).

The degree of nonrandom associations, or linkage disequilibrium, between loci coding abundant proteins in natural populations is unknown. Since a large number of gene products are revealed in a single 2-DE gel, the multilocus genotype array of each individual can be directly inferred. From these 2-DE multilocus genotype data, maximum likelihood estimates of haplotype frequencies can be obtained and, therefore, associations between genetic polymorphisms can be detected in a random mating population (Excoffier and Slatkin, 1995; Slatkin and Excoffier, 1996; Weir, 1996). Furthermore, the extent of linkage disequilibrium between gene markers produced as a result of various evolutionary forces such as mutation, drift, selection or admixture during the evolutionary history of a population, can be used indirectly to infer how strongly these markers are linked on the same chromosome. If the linkage disequilibrium of the markers was created a long time ago, a strong linkage disequilibrium detected now may suggest close physical linkage between the markers, because linkage disequilibria decay with time. This principle is the basis of linkage disequilibrium mapping, an approach with a great potential to obtain information on physical linkage, which is extensively used with molecular markers (Jorde, 1995; Kaplan et al, 1995; Weir, 1996; Wu and Zeng, 2001). In this article, the first attempt to detect linkage disequilibrium between loci coding abundant proteins as detected by 2-DE is attempted in the marine mussel M. galloprovincialis.

Materials and methods

Mussel sampling and two-dimensional gel electrophoresis

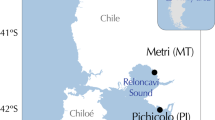
Adult mussels were sampled from two M. galloprovincialis populations in the NW of the Iberian Peninsula in November 1998: a midintertidal population from a wave-exposed rocky shore in Ribadeo and a raft-cultured population from an inner cultivation area in the Ría de Arosa (Vilagarcía, Figure 1). Mussels were brought alive to the laboratory, where they were dissected. The foot was removed from each individual and frozen, lyophilized and stored at −80°C. Proteins were extracted by suspending 30 mg of lyophilized tissue in 1 ml of O'Farrell lysis buffer (9.5 M urea, 2% NP-40 (v/w), 2% ampholytes pH 7–9 and 100 mM dithiothreitol (DTT)). The mixture was shaken for 4 h at 30°C and centrifuged at 12000 × g for 30 min.

Figure 1
figure 1

Map of the NW coast of the Iberian Peninsula showing the sampling sites of M. galloprovincialis.

Full size image

2-DE of mussel foot was performed as described by López et al (2001). Protein loads of 127 and 255 μg (in order to study the less abundant proteins) were applied to each gel. In this way, at least two gels were run for each of the individuals analysed. Isoelectric focusing using carrier ampholytes was carried out at 200 V for 2 h, 500 V for 2 h and 800 V for 16 h. Second dimension electrophoresis was carried out at 25 mA per gel for 1.5 h followed by 35 mA per gel for 5 h. 2-DE gels were stained by the silver technique of Morrisey (1981).

Data analysis

Genotype frequencies were determined by direct count on the gels. Goodness-of-fit of genotype frequencies to Hardy–Weinberg proportions at each locus was tested by means of the χ2 and the exact test. The exact test is very useful when the sample size and/or some genotype frequencies are small because it does not rest on asymptotic approximations for large samples (Louis and Dempster, 1987; Guo and Thompson, 1992). Departures from Hardy–Weinberg proportions were measured by two FIS statistics: the fC of Weir and Cockerham (1984) and the fT of Robertson and Hill (1984). The ratio of the estimate squared of fT to its variance was used as a test for FIS=0 with one degree of freedom, which is optimal for detecting Hardy–Weinberg deviations in terms of statistical power (Robertson and Hill, 1984; Rousset and Raymond, 1995). Unbiased estimates of expected heterozygosity for single loci (h) and the population average heterozygosity (H), calculated as the average of h over all loci, were computed according to Nei (1978). The degree of genetic variation among populations was measured by means of the coefficient of gene differentiation (GST) as defined by Nei (1973), (1986).

Haplotypic frequencies for locus pairs were estimated from genotypic data using the expectation-maximization (EM) algorithm (Dempster et al, 1977; Excoffier and Slatkin, 1995). Computation of linkage or gametic disequilibrium from haplotypic frequency estimates was accomplished taking into account that many of the protein loci analysed are multiallelic (Weir and Cockerham, 1978; Weir, 1996). In this way, a separate disequilibrium coefficient Dij is defined for each pair of alleles, Ai and Bj at loci A and B, respectively, as Dij=Xij − pi qj, where Xij is the frequency of gamete Ai Bj and pi and qj are the corresponding allele frequencies. A normalized measure of the extent of gametic disequilibrium for each pair of alleles is computed as D′ij=Dij/Dmax (Lewontin, 1964), where Dmax=min[piqj, (1−pi)(1 −qj)] when Dij<0 or Dmax=min[pi(1−qj),(1 −pi)qj], when Dij>0. The extent of overall disequilibrium between all the alleles at two loci is measured by D′=∑i=1k ∑j=1l piqj∣D′ij∣, where k and l are the number of alleles in loci A and B, respectively (Hedrick, 1987; Zapata et al, 2001). The statistical significance of gametic disequilibrium for a particular allelic pair is performed by the χ2 statistic χij2=2NDij2/pi(1 - pi)qj(1 - qj) with one degree of freedom, where N is the number of sampled individuals (Weir and Cockerham, 1978; Weir, 1996). The overall hypothesis that none of the Dij is different from zero was tested by means of χ2 tests χij2) for each one of the allelic pairs with Bonferroni correction for multiple tests (Zapata et al, 2001). Also, a likelihood ratio test was computed as an overall test for gametic disequilibrium between loci (Slatkin and Excoffier, 1995).

Analysis of departures from Hardy–Weinberg proportions (exact test and FIS statistics) was performed using GENET-2 and GENEPOP v. 3.1 programs (Quesada et al, 1992; Raymond and Rousset, 1995). Estimation of haplotypic frequencies from genotypic data by means of the EM algorithm and computation of the likelihood ratio test were performed by the ARLEQUIN program (Schneider et al, 2000). The EM algorithm was always started from 100 random initial haplotype frequencies, to avoid nonconvergence problems in the iterative process and to ensure finding the global maximum likelihood estimate (Excoffier and Slatkin, 1995). The significance of the likelihood ratio test was based on the empirical distribution of likelihood ratios under the null hypothesis of gametic equilibrium generated from 20 000 randomizations, that is, random permutations of alleles at each locus (Slatkin and Excoffier, 1996).

Results

The protein pattern revealed by two-dimensional gel electrophoresis of an individual foot sample of M. galloprovincialis is shown in Figure 2. In any given gel, approximately 1 200 polypeptide spots could be routinely visualized by general protein staining. Our analysis was limited to a subset of 86 polypeptides selected on the basis of three criteria: (i) reproducibility, (ii) intensity and (iii) relative isolation on the gel (Rosenblum et al, 1983,1984; Asakawa et al, 1985; Hanash et al, 1986a,1986b). The choice of spots was made by two investigators who had not previously scored any of them with respect to variability, that is, selected in an unbiased fashion. With respect to reproducibility, spots at the margins of the gel were discarded because of variable migration. The criterion for intensity was that if genetic variation were to result in two spots instead of one (ie a heterozygote), both spots would have a staining intensity above the background. With respect to isolation, spots in crowded regions or spots associated with streaking were not included in the analysis. We arbitrarily assign numbers to the spots to be analysed, working from the upper left to the lower right of the gel. All gels were scored independently by two investigators.

Figure 2
figure 2

Two-dimensional protein pattern obtained from the foot of M. galloprovincialis. Numbers identify the 86 polypeptides analysed and letters (a=acidic, b=basic spot) indicate polypeptides for which variants were observed. The pI is indicated on the horizontal axis and the molecular weight on the vertical axis.

Full size image

Genetic polymorphisms were detected as position mobility shifts due to charge alteration. All the putative polymorphisms exhibited gene dosage dependence in heterozygotes, which is consistent with a genetic basis. As an example, various genetic polymorphisms are illustrated in Figure 3. Allelic variants were named from the basic side of the gel to the acid one. Of the 86 protein spots examined, 32 and 26 exhibited genetic polymorphisms in the Ribadeo and Vilagarcía samples, respectively. The positions on the gel of the polypeptides scored in this study and the identity of five of them, determined by mass spectrometry (López et al, 2001), are indicated in Figure 4.

Figure 3
figure 3

Examples of three genetic polymorphisms. From left to right, the acidic homozygote, the heterozygote and the basic homozygote are displayed. Arrows point to the location of absent and present allelic variants.

Full size image
Figure 4
figure 4

Schematic representation of the 86 polypeptides analysed. Polymorphic variants are joined with a line. The most frequent allelic variants are in black and the rarer are in grey. Monomorphic proteins are outlined.

Full size image

Genotype frequencies and analysis of Hardy–Weinberg deviations for the polymorphic protein loci in the Ribadeo and Vilagarcía samples are shown in Table 1 and Table 2, respectively. Only three of a total of 32 polymorphic loci showed statistically significant departures from Hardy–Weinberg expectations in the Ribadeo sample. Locus 2 showed a significant heterozygote deficiency (fT=+0.490, P< 0.01; X2=6.47, P< 0.01; exact test, P=0.10), while a significant heterozygote excess (fT= −0.430, P< 0.05; X2=5.81, P< 0.05; exact test, P=0.03) was found for locus 48. For locus 46, statistically significant deviations were not detected by the fT and the χ2 tests (fT=+0.171, P>0.05; X2=5.74, P> 0.05) but the probability of the exact test was 0.0497 and a statistically significant heterozygote deficiency was detected for allele 20 at this locus (fii=+0.424, P< 0.05). In the Vilagarcía sample, only two loci (6 and 76) present statistically significant deviations from Hardy–Weinberg proportions (fT=+0.703, P< 0.05, for both loci). When a Bonferroni correction is applied in each sample to control for potential Type I errors due to the use of multiple tests, statistical significance of Hardy–Weinberg deviations is not found for any of these five loci. The deviations from Hardy–Weinberg expectations expressed by means of the two FIS statistics, fC and fT, displayed similar values in both samples. In the Ribadeo sample, fC ranged from –0.426 to 0.478 and fT varied between −0.430 and 0.490 across loci. The mean values over loci were −0.004 pm 0.018 and −0.011 pm 0.016 for fC and fT respectively. In the Vilagarcía sample, fC ranged from –0.581 to 0.632 and fT varied between −0.571 and 0.703, the average values being −0.065 ± 0.032 and −0.033 ± 0.032, respectively. In both samples, the averages of fT and fC estimated from 2-DE polymorphisms are very close to the heterozygote excess expected by sampling from a population in Hardy–Weinberg equilibrium, which is FIS=−(1/(2N - 1)) (Kirby, 1975; Robertson and Hill, 1984). Thus, the FIS value expected by sampling is −0.017 for Ribadeo (N=30) and –0.066 for Vilagarcía (N=8). It appears, therefore, that genotype data are generally consistent with their Hardy–Weinberg proportions for the Ribadeo and Vilagarcía populations, although significant deviations could be occurring in some specific loci, particularly towards a deficiency of heterozygote genotypes. Heterozygote deficiency is a common observation from several species of marine molluscs and has been described in M. galloprovincialis for some allozyme loci (Sanjuan et al, 1990,1994; Raymond et al, 1997). Although no satisfactory explanation for this observation has yet been identified, the possibility that locus-specific factors such as selection or Wahlund effect are involved has been suggested (Raymond et al, 1997).

Table 1 Genotypic frequencies for 32 polymorphic protein loci in the Ribadeo population sample. Deviations from Hardy–Weinberg proportions are measured by the FIS statistics, fC of Weir and Cockerham (1984) and fT of Robertson and Hill (1984). Statistical significance of these deviations is evaluated by the test based on fT estimator (Robertson and Hill, 1984), the χ2 test and the exact probability test
Full size table
Table 2 Genotypic frequencies for 26 polymorphic protein loci in the Vilagarcía population sample. Deviations from Hardy–Weinberg proportions are measured by the FIS statistics, fC of Weir and Cockerham (1984) and fT of Robertson and Hill (1984). Statistical significance of these deviations is evaluated by the test based on fT estimator (Robertson and Hill, 1984), the χ2 test and the exact probability test
Full size table

Indexes of genetic variability (expected heterozygosity, degree of polymorphism and number of alleles per locus) for the Ribadeo and Vilagarcía population samples are given in Table 3. Patterns of polymorphism characterized by the number and the frequency of the protein variants were similar in the two population samples. The Ribadeo sample showed 54 monomorphic and 32 polymorphic loci (16 loci with two, 12 loci with three and four loci with 4 alleles) while the Vilagarcía sample presented 60 monomorphic and 26 polymorphic loci (17 loci with two, 5 loci with three and 4 loci with four alleles). The estimates of genetic variation were also very similar for both populations. Average heterozygosity was 0.101±0.018 and 0.114±0.021 in Ribadeo and Vilagarcía, respectively. The degree of gene differentiation (GST) between the two populations for single loci ranged from 0 (locus16) to 0.544 (locus 23) and the GST estimated for the whole loci set was 0.067. These estimates are higher than those reported for natural mussel populations of the Atlantic coast of the Iberian Peninsula based on allozyme data (Quesada et al, 1995). This could be due to the small sample size of the Vilagarcía sample as well as to the sampling process associated with mussel culture in rafts from individuals collected in natural populations.

Table 3 Estimates of genetic variability from 2-DE in two populations of Mytilus galloprovincialis
Full size table

A total of 406 two-locus associations were evaluated from 29 polymorphic loci of the Ribadeo population sample. Loci 2, 46 and 48 were not included in this analysis since Hardy–Weinberg departures were found at these three loci, and the maximum likelihood estimation of haplotype frequencies is based on the assumption of Hardy–Weinberg proportions (Hill, 1974; Excoffier and Slatkin, 1995). Statistical significance for gametic association between loci was detected in 18 pairs (4.43%) by the likelihood ratio test and in 81 pairs (19.95%) by χ2 tests (with Bonferroni correction) for each pair of alleles. When using a single χ2 test for the most frequent alleles at a given locus pair, significant associations were detected in 53 locus pairs (13.05%). Overall, 92 (22.66%) of 406 pairs of loci show statistically significant associations as detected by some of the different tests. Our results show that the χ2 tests detect more significant gametic associations than the likelihood ratio test. However, it must be emphasized that the statistical power for detecting significant gametic disequilibrium by the χ2 test is not large, particularly when allelic frequencies are extreme and disequilibrium is not relatively intense (Brown, 1975; Zapata and Alvarez, 1992). This must be particularly considered in our case, given that the sample size is not large (2N=60). In general, two broad patterns of gametic disequilibrium can be observed in those pairs of loci where statistically significant associations are detected by tests. In 53 locus pairs, the statistical association is mainly due to the most frequent alleles, while in 39 locus pairs gametic disequilibrium is associated only with rare alleles (alleles at a low or intermediate frequency). In the first type of locus pair, the magnitude of gametic disequilibrium detected is high for the overall disequilibrium (D′=0.687±0.036) and for the disequilibrium of the most frequent alleles (|D′ij|=0.699±0.037), while in those locus pairs where statistically significant disequilibrium is due to rare alleles, the extent of disequilibrium observed is clearly lower for both the overall disequilibrium (D′=0.411±0.040) and the disequilibrium exhibited by the most frequent alleles (|D′ij|=0.334±0.045).

From the disequilibrium analysis, groups of loci are detected in which all pairwise combinations exhibit statistically significant gametic disequilibrium. One of these clusters involving six loci (8, 17, 24, 39, 79 and 80) is shown in Table 4. Overall D′ for locus pairs in this cluster ranges from 0.224 to 1 with a mean value of 0.561±0.088. In addition, three loci of this cluster (39, 79 and 80) show significant associations between the most frequent alleles for all pairwise combinations (D′ij for the most frequent alleles ranging from 0.621 to 1). Also, a cluster involving four loci (58, 76, 79 and 80) has been detected (Table 5). Overall D′ for locus pairs in this cluster varies from 0.365 to 0.636 with an average value of 0.506±0.041. In this cluster, all pairwise combinations show significant associations between the most frequent alleles (D′ij range from 0.326 to 0.621). Other clusters involving three or four loci have also been detected.

Table 4 Cluster of six loci (8, 17, 24, 39, 79 and 80) showing statistically significant associations between all pairs. For each locus pair, the overall D′ and the number of statistically significant χij2 over the number of total χ2 (in parentheses) are indicated in the upper line; the |D′ij| and the χij2 values for the most frequent alleles (in parentheses) are shown in the lower line
Full size table
Table 5 Cluster of four loci (58, 76, 79 and 80) showing statistically significant associations between all pairs. For each locus pair, the overall D′ and the number of statistically significant χij2/number of total χ2 (in parentheses) are indicated in the upper line; the |D′ij| and the χij2 values for the most frequent alleles (in parentheses) are shown in the lower line
Full size table

Discussion

2-DE has been used to measure the degree of genetic variability for loci coding abundant proteins in the marine mussel M. galloprovincialis. Among the 86 polypeptides selected in an unbiased fashion for scoring for genetic variability, the natural population sample from Ribadeo exhibited such variation in 32 (37.2%) polypeptides with an average heterozygosity of 0.101±0.018. Similar results were obtained in a cultured population from Vilagarcía (P=30.2%, H=0.114±0.021). These estimates of heterozygosity are clearly higher than those previously reported by 2-DE for animal populations (see Table 6) and put M. galloprovincialis as the animal species with the highest genetic variability detected by 2-DE to date. M. galloprovincialis heterozygosity is nearly six-fold higher than the heterozygosity values of Drosophila (average of heterozygosity estimates from different studies weighted by the number of loci scored is 0.021 and 0.023 for D. melanogaster and D. simulans, respectively), mouse (0.020), cheetah (0.013) and man (weighted average from different tissues is 0.017). Our findings clearly show a need to extend the 2-DE analysis to an increased number of species in order to obtain a wider view on genetic variability for loci responsible for abundant proteins in natural populations.

Table 6 Estimates of genetic variability from two-dimensional and single-dimensional electrophoresis in animal species
Full size table

When comparing 2-DE and 1-DE estimates of heterozygosity for different animal species, two aspects deserve consideration (see Table 6). Firstly, although the 2-DE data set is still not large, the range of variation of heterozygosity estimates for different animal species seems to be clearly smaller than that reported from allozymic data. In mammals, for example, the allozyme heterozygosity varies from 0 up to 22% in 321 species reviewed by Makarieva (2001). It has been shown that these variations can be mainly explained by differences in the number of loci studied (Makarieva, 2001). From this perspective, the larger number of loci analysed by 2-DE with respect to 1-DE could be one of the reasons explaining the small variation in 2-DE estimates of heterozygosity among animal species. Second, although 2-DE variation is generally reduced, it parallels the allozymic data in that more variable species, as indicated by 1-DE, are also shown to be more variable from 2-DE analysis (see Table 6). In fact, there is a statistically significant correlation (r=0.838, d.f. 4, P<0.05) between heterozygosity estimates yielded by both techniques among the species included in Table 6. Two alternative explanations for this discrepancy, not mutually exclusive, have been widely discussed in the literature (Edwards and Hopkinson, 1980; Aquadro and Avise, 1981; Wanner et al, 1982; Mc Lellan et al, 1983; De Vienne et al, 1996). For one, the group of proteins analysed on 2-D gels is intrinsically less variable than the soluble enzymes and proteins previously studied. For another, the technique of 2-DE is not capable of resolving many variants that are detectable by the conventional electrophoretic methods, since proteins are denatured and some differences of conformational nature could remain undetectable. In this respect, Wanner et al (1982) tested the ability of 2-DE to resolve the allelic variants of five loci previously studied by 1-DE. 2-DE could resolve more than 90% of the variants originally detected by 1-DE (16 of the 17). The unique allelic variant that remained undetectable for 2-DE was attributed to a conformational variation. Furthermore, DNA sequence analysis for different electrophoretic classes at several enzyme loci (Adh, Gpdh, Sod, Est-5, Est-6 and Xdh) in Drosophila has revealed that most differences (75–100%) in protein mobility detected by single electrophoresis are due to variations in the net charge of the protein (Riley et al, 1992; Veuille and King, 1995; Barbadilla et al, 1996). Therefore, because the conformational variations in protein structure seems to play a minor role in the electrophoretic mobility, the remarkable reductions in the level of variability detected by 2-DE with respect to 1-DE, ranging from 58 (M. galloprovincialis) to 85.2% (man) from data in Table 6, can hardly be attributed to conformational changes undetected by 2-DE. This suggests that the more feasible explanation for the lower levels of genetic variability detected by 2-DE is that the group of proteins analysed by this technique is intrinsically less variable than the enzymes assayed by 1-DE.

Among a total of 406 two-locus pairs analysed for detecting linkage disequilibrium in the Ribadeo population sample, 92 show statistically significant associations. This is a quite large proportion (22.7%), taking into account that the size of the studied sample is not very large (2N=60) and the statistical power of tests for detecting gametic disequilibrium is low when allelic frequencies are extreme or the disequilibrium is not relatively intense (Brown, 1975; Zapata and Alvarez, 1992). Furthermore, information on physical linkage between some protein loci can be extracted from the disequilibrium analysis. Thus, clusters of loci showing statistically significant disequilibrium between all the locus pairs have been found (Table 4 and 5). In some cases, the significant disequilibrium is associated with rare alleles. In these cases, a strong linkage disequilibrium detected between two genetic loci may be due to the recent occurrence of disequilibrium rather than a close physical linkage of the two loci, since rare alleles are most likely to have arisen recently in the population by the introduction of new mutations. Most interesting are those cases where the significant disequilibria are associated with the most frequent alleles which are old alleles. Although there are many evolutionary forces that can cause an association between the alleles at different loci, the decay of genetic disequilibrium along generations is expected to be smaller for increasing physical linkage and it provides the rationale for inferring physical linkage from linkage disequilibrium (Jorde, 1995; Kaplan et al, 1995; Weir, 1996; Wu and Zeng, 2001). On this basis, a cluster of four loci (58, 76, 79 and 80, Table 5) and several clusters of three loci (39, 79 and 80, Table 4 and data not shown) where statistically significant disequilibria are occurring between all pairwise combinations for common alleles have been found. It is very likely that some physical linkage must be occurring between those protein loci included in clusters. This information will be very useful for planning future experiments of linkage analysis from single-pair matings. The previous knowledge of sets of protein loci where physical linkage is present can be very useful in selecting informative families for traditional linkage analysis (Weir, 1996). To date, the available information on linkage of genetic markers is very scarce in marine mussels (Beaumont, 1994), so that investigations on this issue will be of great interest.