Main

Glioblastoma (Gb) (grade IV glioma) is the most malignant form of human brain tumour (Kleihues and Cavenee, 2000). Even that the incidence of this cancer is low compared with other human cancers (Louis et al, 2007), the fatal outcome associated with its diagnosis has motivated in the past years intensive research in its molecular transcriptomic profile. This previous work demonstrated that molecular (or gene) signatures obtained from microarray experiments allow a better characterisation of the pathology than the current clinical scheme based on histopathological classification (Nutt et al, 2003; Freije et al, 2004; Phillips et al, 2006). That is, molecular signatures are a better predictor of the patient survival time than the diagnosis provided by histopathology. Nutt and Freije in their respective works showed that there may be two main groups with differential survival time: one composed of anaplastic gliomas (grade III) and Gbs (grade IV), and another one almost fully composed of Gbs. Later on, Phillips et al (2006) also showed that glial tumours can be molecularly divided into three different profiles: proneural, mesenchymal and proliferative. The validity of these profiles was evaluated on a larger data set composed of Gbs from various hospitals and different types of Affymetrix microarrays (Lee et al, 2008). However, Lee and collaborators found that only the proneural profile patients displayed a longer survival time compared with the rest of molecular groups. On the other hand, a prognosis predictor was proposed to identify mesenchymal and proneural-like Gbs based on the low or high expression of nine genes, respectively (Colman et al, 2010). This body of molecular phenotyping work has contributed to generate an eventual consensus around the hypothetical distinction of gliomas based on these three profiles mentioned (proneural, mesenchymal and proliferative). In parallel, these profiles have been related to the type of stem cells from which Gbs may arise (Beier et al, 2007; Günther et al, 2008; Liu et al, 2009; Lottaz et al, 2010). Moreover, Gb cases showing mutation of a specific locus of IDH1 and non-amplification of EGFR gene have been related to a better prognosis (Parsons et al, 2008; Gravendeel et al, 2009; Yan et al, 2009; Verhaak et al, 2010).

All these findings provide hope that prognosis of Gbs may be improved based on the molecular features. However, a consensus molecular signature that incorporates all these different findings into an improved predictor to discriminate Gbs with respect to prognosis (i.e., survival) is still lacking. To achieve this goal, microarray data from various centres should be combined, different data sets should be used to develop the molecular signature and the outcome should be validated with an independent data set, ideally from a different centre (Altman and Royston, 2000; Dupuy and Simon, 2007). Three previous studies partially fulfilled these criteria considering data from various centres (Lee et al, 2008; Colman et al, 2010; Lottaz et al, 2010), but only Colman and collaborators validated their results using an independent test set. In fact, they classified cases based on their proposed signature and demonstrated that such a classification resulted into two groups with differential survival. However, they did not estimate the prediction ability of their signature through a leave-one-out cross-validation (LOOCV) or by classification of cases from an independent test set through a discriminant equation, as various authors performed to molecularly distinguish high-grade gliomas (Nutt et al, 2003; Petalidis et al, 2008; Li et al, 2009; de Tayrac et al, 2011). The absence of such estimation may cause problems for other groups to predict new local Gb cases based on these signatures. Verhaak et al (2010) validated their results on an independent data set, but the rule used to classify new cases was based on a signature composed of 840 genes. Although this is a valid method to classify new cases, the large amount of genes required excludes the possibility of developing a discriminant linear equation due to colinearity problems and would complicate the implementation on day-to-day diagnostic protocols.

Accordingly, the purpose of our study was first to produce a probeset-based equation, as we already performed in two previous works for a different problem (Castells et al, 2009, 2010), that could distinguish Gb subgroups. Second, to assess the performance of our local equation, we generated another probeset-based equation using the gene signatures proposed by Lee and Colman in their respective works (Lee et al, 2008; Colman et al, 2010). The differential status of IDH1 mutation and EGFR amplification found between groups stratified by our local signature-based equation (LocSBE) and Colman signature-based equation (ColSBE), suggests that the two groups of Gbs identified here may correspond to the classical primary and secondary Gbs. However, only ColSBE provided two groups that displayed a significant survival difference, as well as a differential percentage of cases showing both expected methylation of gene MGMT promoter and overexpression of gene VEGF.

Materials and methods

Collection, storage and histopathology analysis of prospectively acquired samples

Collection of biopsies was carried out at different hospitals from the Barcelona metropolitan area through the European Union-funded eTUMOUR (http://www.etumour.net) and HealthAgents (González-Vélez et al, 2007) projects and the Spanish-funded MEDIVO2 project.

A total of 44 biopsies were collected from the Hospital Universitari de Bellvitge (L’Hospitalet de Llobregat), two biopsies from the Hospital Universitari Germans Trias i Pujol (Badalona) and one biopsy from the Hospital Sant Joan de Déu (Esplugues de Llobregat). Among the 47 biopsies included in this study, 46 were Gbs and 1 was gliosarcoma, and their diagnosis was directly obtained from the Histopathology ward of the participating hospitals (local data set from now on). The full study protocol was approved by the local Ethics Committees and informed consent was obtained from all patients.

An aliquot of tumour was snap frozen in liquid nitrogen until RNA isolation. Another aliquot was fixed in 4% buffered formalin and embedded in paraffin. For routine histological examination, 4-μm thick sections were stained with haematoxylin and eosin (H&E). Both, the WHO 2000 and 2007 Nervous System Classification criteria (Kleihues and Cavenee, 2000; Louis et al, 2007) were used for diagnosis, since biopsies were collected from 2004 until 2008.

RNA isolation

Total RNA from frozen biopsies stored in liquid nitrogen was isolated following the procedure indicated by the manufacturer using the mirVana RNA isolation kit (Ambion-Life Technologies, Grand Island, NY, USA). RNA was characterised using a NanoDrop spectrophotometer (NanoDrop Technologies, Wilmington, DE, USA). Absence of protein contamination was monitored by the 260/280 nm ratio of absorbance, and samples with a ratio ranging between 1.6 and 2.0 were accepted for further processing. Integrity of the RNA was assessed by using the capillary electrophoretic system 2100 Bioanalyzer (Agilent, Santa Clara, CA, USA). Only samples producing a 28S/18S ratio equal or higher than 1.2 or an RNA integrity number (RIN) number equal or higher than 6 were used for further analysis. This was as agreed in the consensus protocols for data acquisition in the eTUMOUR project.

Microchips and real-time PCR (RT–PCR)

Labelling and hybridisation onto microchips was performed at the Affymetrix core facility of the Institut de Recerca de la Vall d'Hebron (Barcelona). Labelling was performed using the One-Cycle Target Labelling and Control Reagents kit (Affymetrix, Santa Clara, CA, USA). The starting material for the labelling protocol ranged from 1.5 to 5 μg of total RNA and the resulting labelled cRNAs were hybridised onto the HG-U133 plus 2.0 GeneChip (Affymetrix). Fluorescence images were obtained by scanning the microchips with the software provided with the GeneChip Scanner 3000.

We used a two-step procedure for the RT–PCR experiments. One microgram of total RNA was used for retrotranscription using the iScript cDNA synthesis kit (Bio-Rad, Hercules, CA, USA). A 1/20 dilution of the obtained cDNA was used for amplification with the SsoAdvanced SYBR Green supermix on the CFX96 Real-Time System (Bio-Rad). We analysed the expression of four genes using specific primers designed by us: CHI3L1 (forward-CTGTGGGGATAGTGAGGCAT, reverse-TAGGATGTTTGGCTCCTTGG), LDHA (forward-CACAGCTATATCCTGATGCTGG, reverse-GACTAGGCATGTTCAGTGAAGGAG), LGALS1 (forward-CTAAGAGCTTCGTGCTGAACCTG, reverse-ATGCACACCTCTGCAACACTTC) and IGFBP3 (forward-AGGGCACTCTGGGAACCTAT and reverse-CTCTCTGTCCCTCCTACCCC). Five samples per Gb group were evaluated and triplicates per each sample–gene pair were performed. Fold changes were computed following a method based on the relative difference between groups (Livak and Schmittgen, 2001).

Normalisation of data and acquisition of publicly available data sets

All data considered in this work were normalised using the robust multi-array average (RMA) method, which is available in the affy package from the R software (Irizarry et al, 2003). We initially used as a test data set the data made publicly available in the work of Lee et al (2008) (Lee’s data set from now on, GSE13041, Gene Expression Omnibus; http://www.ncbi.nlm.nih.gov/gds). We selected for our study those 218 out of the 267 Gbs available that were hybridised onto either the Affymetrix microchips HG-U133A (n=191) or HG-U133 plus 2.0 (n=27), since the probeset annotation of the remaining 49 Gbs (HG-U95 Av2) did not match with the one from the other types of microchips. We evaluated two signatures: one composed of 377 probesets described in Lee’s work (Lee’s signature, from now on), and a second one provided by Colman and collaborators (Colman’s signature, from now on). This signature was derived from 110 cases published in four previous works (Nutt et al, 2003; Freije et al, 2004; Nigro et al, 2005; Phillips et al, 2006). Probeset identifiers of the 38 genes proposed in Colman’s work were not provided, since the signature was mainly evaluated using RT–PCR. For this reason, we used those 36 matching genes in both HG-U133A and HG-U133 plus 2.0 microarrays, which corresponded to 63 probesets in both microarray types. For the second part of the study, we used data made publicly available by Gravendeel et al (2009), Gravendeel’s data set from now on (GSE16011). Among available data sets containing Gbs, uniquely this one provides a large number of cases (n=73) with survival and KPS data, as well as status of both IDH1 mutation and EGFR amplification. We used those 71 Gbs that had survival time and living status available.

Feature selection for the unsupervised classification

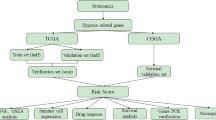
We selected those 100 probesets with the highest coefficient of variation (CV) and at least 30% of signals higher than 1000, a.u. of fluorescence among Gbs from our local data set. Probesets from each signature were used as input for a hierarchical cluster using the default settings of the heatmap_2 function from the Heatplus R package (R Development Core Team, 2011), but we used the ‘Manhattan’ distance and the ‘Ward’ clustering method, as described in a previous work (Tortosa et al, 2011). In doing so, we obtained a heatmap with probesets grouped in rows and cases in columns. Those cases that were clustered together in a given branch were assigned to one group of Gbs. The optimal number of groups of Gbs was determined using the k-means method by setting the number of clusters to 2, 3, 4 or 5. The reliability of such clusters was assessed through the computation of the silhouette statistic from the cluster R package (Hartigan and Wong, 1979). The closest to 1, the highest the dissimilarity between clusters of cases is (Rousseeuw, 1987). For our unsupervised signature, the expression difference between groups of Gbs was assessed by computing the q-value for all probesets in our local data set (Storey and Tibshirani, 2003). We provide a graphical summary of this section in Supplementary File 1A. An overview of this and next sections is depicted in Figure 1.

Figure 1
figure 1

Diagram of analyses performed. This figure provides an overview on data analysis performed in this work. Computations are described inside empty rhombus, data sets indicated inside a gridded box and groups of probesets depicted inside a grey box. Analyses downstream grey boxes were performed separately for each signature (Local, Lee’s or Colman’s signatures). Standardisation Lee’s values denotes standardisation of local data set using mean and standard deviation values from Lee’s data set. The estimated prediction indicated inside a circle filled with dots corresponds to the error obtained by comparing classifications produced by hierarchical cluster and LDA equations. HC is an abbreviation for hierarchical cluster, LOOCV LDA means leave-one-out cross-validation based on LDA, 4 discriminant probesets indicates that those four most discriminant probesets across LOOCV were selected and IDH1/EGFR alterations corresponds to the percentage of cases showing IDH1 mutation/EGFR non-amplification per Gb group.

Full size image

Survival analysis

Analyses described in this section were performed using the default settings of the survival package from the R software (R Development Core Team, 2011). We fitted a survival curve for each molecular group of Gbs using the Kaplan–Meier estimate (function survfit). We included in this analysis either patients for which the date of death was recorded or those patients alive, but for whom a follow-up time of at least half a year was recorded. The difference between the fitted Kaplan–Meier curves was assessed using the Mantel–Haenszel test (function survdiff) (Harrington and Fleming, 1982). A description of survival data is provided in Supplementary Table 1.

On the other hand, we fitted a Cox’s proportional hazards model (function coxph) using Gravendeel’s data set (Supplementary Table 6). Models were fitted using as a factor the Gb group provided by the four probeset-based equation that detected the highest survival difference on Gravendeel’s data set. However, we also fitted a Cox’s proportional hazards model in Gravendeel’s data set for the variables IDH1 and EGFR status, LOH of chromosomes 1p and 19q, age, gender, administration of chemotherapy and radiotherapy, surgery type, and KPS. In contrast, we fitted a Cox’s proportional hazards model in Lee’s data set for the same variables than before, except KPS and IDH1 and EGFR status, but we included the Gb group as assigned by Lee and collaborators, status expression of genes MGMT, VEGF and EGFR, and complementary administration of temodar (Supplementary Table 6). Therapy-related variables (chemotherapy, radiotherapy and temodar) in Lee’s data set and radiotherapy administered in Gravendeel’s data set only indicated those patients subjected to the therapy. The rest of the values were missing and we assumed that those missing values corresponded to patients not subjected to therapy. The significance of each variable was assessed using Wald’s test and the 95% confidence intervals for the hazard ratio were reported.

Evaluation of the predictive ability of gene signatures on the local data set

We considered three signatures in this work: (1) our local unsupervised signature, (2) Lee’s signature and (3) Colman’s signature, as described above. We tested the predictive ability of these signatures by performing an LOOCV on our local data set. We standardised the expression values using the mean and standard deviation of each probeset, and assigned the group to each sample by performing a hierarchical cluster, as previously explained. The grouping provided by the hierarchical cluster was considered as the ‘gold-standard’ for classification purposes in this and next section. For each gene signature evaluated, we selected those four probesets with the highest fold change among differentially expressed genes (P-value<0.05, Wilcoxon rank-based test after Bonferroni correction) among training samples (all except the sample left out). At each iteration, these probesets were used to calculate a linear discriminant analysis (LDA)-based formula using the lda function from the R package MASS (R Development Core Team, 2011). This function produced an additive model composed of four variables (four probesets), each one with a discriminant coefficient. We predicted the group of the case left out from the training set by using the discriminant scores, which we obtained by multiplying the discriminant coefficients from the lda function and the standardised expression values of each probeset. The discriminant threshold used was 0, since this value is the expected centroid between the two groups by using this approach. We repeated this procedure as many times as cases were available in the data set. In case there were no probesets below the Bonferroni threshold, we selected those four probesets that displayed the highest fold changes. We saved the name of the four probesets selected at each iteration, so that we could summarise the most discriminant ones. Accuracy, sensitivity and specificity were computed from test sample results. We provide a graphical summary of this section in Supplementary File 1B.

Development of a predictive equation

Considering that the predictive ability of each formula was going to be initially tested on Lee’s data set, we standardised the expression values of our local and Lee’s data set using the mean and standard deviation of Lee’s data set, as we previously described (Castells et al, 2010). We reassigned the group of cases (both local and Lee’s data sets) through hierarchical clustering using the four most relevant probesets from each signature. We generated a discriminant formula only using our local data set and the four most frequently selected probesets across the LOOCV, with highest fold change and the lowest P-value. This equation was used to predict the group of each case from Lee’s data set as described in the previous section. Accuracy, sensitivity and specificity obtained from Lee’s data set were considered as the estimated predictive ability of each discriminant formula. We provide a graphical summary of this section in Supplementary File 1C. The discriminant ability of equations generated was tested using Gravendeel’s data set. The difference between the percentage of cases showing both IDH1 mutation and non-amplification of EGFR in each Gb subtype was assessed using Pearson’s χ2-test and considered significant for a P-value under 0.05. Other molecular and clinical variables (LOH of chromosomes 1p and 19q, therapy, age, gender and KPS) were also evaluated (Supplementary Figures). Similarly, Lee’s data set was used to evaluate the performance of equations on clinical (collection centre, therapy, age and gender) and molecular (expression of genes MGMT, VEGF and EGFR, and molecular cluster) variables available. As for Cox’s models, we assumed no therapy administered for those cases showing missing values in therapy variables (chemotherapy, radiotherapy and temodar). In Supplementary Figures, difference between groups for numeric variables (age and KPS) was assessed using a t-test and considered significant for a P-value under 0.05.

Results

Unsupervised analysis to detect molecular subgroups of Gb

Our unsupervised signature composed of 100 probesets obtained the highest values of the silhouette statistic when we set the number of k-means clusters to two (silhouette=0.26). However, not all 100 probesets selected were differentially expressed between the two potential molecular groups of Gb (Supplementary Table 2). For this reason, we selected those 69 probesets that were differentially expressed (q-value<0.05) between the molecular subgroups and repeated the hierarchical cluster, as well as the computation of the silhouette statistic. These 69 probesets resulted in an increased value of the silhouette statistic compared with the previous signature regardless the number of k-means clusters considered, while the optimal one was maintained at two clusters (silhouette=0.34).

The 69 probesets defined one group (group of low expression (GLE) from now on, n=14) of samples that displayed on average low expression values (Figures 2A and B). This means that most cases in GLE displayed lower expression values than the group of high expression (GHE), but not all of them (Figure 2A). Interestingly, a small difference in the average age of patients between groups was found (GLE=51.1±21.2 years and GHE=63.0±9.2 years, P-value=0.078, Wilcoxon rank-based test; Figure 2B). In contrast, neither our local signature detected two groups displaying a different survival time (P-value=0.826), nor did Lee’s and Colman’s signatures (P-value=0.729 and 0.461, respectively; Figure 2B).

Figure 2
figure 2

Summary of unsupervised and supervised analysis. (A) This figure displays the molecular profile of the 69 probesets with the highest CV and with fluorescence signals higher than 1000, a.u. in at least 30% of cases. Also, these probesets are differentially expressed between the two groups of glioblastomas and their expression values are independent from patient’s gender (see also Supplementary Table 1). Columns are Gb cases and rows probesets. The bottom bar indicates the normalised intensity (arbitrary scale) of probesets per sample. (B) We depict the characteristics of groups (GHE and GLE) detected for each gene signature tested on our local non-standardised data set. Three signatures were evaluated: (1) 69 probesets obtained through our unsupervised approach, (2) Lee’s signature and (3) Colman’s signature, which corresponded to 63 probesets. (C) Features obtained by applying each four probeset-based equation on Lee’s standardised data set. GHE means group of high expression and GLE means group of low expression. Differences between groups in both intensity and age were tested using the Wilcoxon rank-based test, while Pearson's χ2-test was used to evaluate differences in the gender ratio between groups.

Full size image

Moreover, some probesets represent genes that have been related to glioma or Gb tumourigenesis: proliferative factors or their receptor (EGR1, IGFBP2, IGFBP3 and VEGFA) (Zhang et al, 2002; Lönn et al, 2008; Norden et al, 2009; Mittelbronn et al, 2009), collagen isoforms (COL1A1, COL1A2 and COL3A1) (Kirsch et al, 2000; Rege et al, 2005), proteins that bind to fatty acids (FABP5 and FABP7) (Mita et al, 2007; Brun et al, 2009) and transmembrane proteins (CD24 and CD163) (Senner et al, 1999; Komohara et al, 2008). Additionally, some genes that are overexpressed in GHE (GBP1, SERPINA3, CD163, TIMP1, CHI3L1, IGFBP2 and FABP5) were also detected by Tso et al (2006) overexpressed in primary Gbs compared with low-grade gliomas. Also, our local signature has 9 genes (11 probesets) in common with Colman’s signature (CHI3L1, COL1A2, FABP5, GRIA2, IGFBP2, IGFBP3, MAOB, NNMT and TIMP1), among which two of these were included in the final signature proposed in their work. Six other genes in our signature correspond to gene isoforms in Colman’s signature (ACTA2, COL1A1, COL3A1, FABP7, SERPINA3 and VEGFA). Similarly, 14 probesets of our local signature matched with those in Lee’s signature (ACTA2, ADM, ANXA1, COL1A2, COL3A1, CD163, DCN, IGFBP2, MGP, NNMT, TIMP1, RCAN1, SERPINA3 and VEGFA).

Evaluation of the predictive capacity of gene signatures on the local data set through LOOCV

The optimal number of case clusters was again two, as assessed by silhouette values (Supplementary Table 3). We obtained the prediction accuracy, the sensitivity and the specificity of GLE for each gene signature. The best prediction in our data set (n=47) was produced by our local gene signature, the second one by Colman’s signature and the third one by Lee’s signature (Figure 2B). In fact, our local and Colman’s signatures displayed a high percentage of probesets differentially expressed (below the Bonferroni threshold) among those selected in the LOOCV (Supplementary Table 4). In contrast, few probesets in Lee’s signature were differentially expressed.

Development of discriminant equations

We selected among probesets used in the LOOCV those four ones from each signature that fulfilled the criteria explained above. The selected probesets were used to perform a hierarchical cluster to assign group membership in Lee’s data set. We built the LDA equation for each signature considering two groups, as indicated by the silhouette statistic, which were called GHE and GLE. In fact, only in Lee’s signature the difference of intensity between means was overlapping and the least significant (see Figure 2C), but we also set the GHE to the group with highest average value. The resulting equations are

LocSBE, LeeSBE and ColSBE represent discriminant scores from Local, Lee or Colman-signature based equation, respectively, and S(x) indicates standardised values of an x probeset of a given gene, as listed in Supplementary Table 5. A negative DSC corresponds to GLE, while a positive one to GHE. An example for the computation of discriminant values for each case is described in Supplementary File 2. Detailed results of this section are provided in Supplementary Tables 3–5.

As shown in Figure 2C, the significantly higher age of patients in GHE compared with GLE in Lee’s data set, regardless the four probeset-based signature used, seems to agree with the results for primary Gbs provided by Tso et al (2006). Indeed, some of the genes or similar isoforms that compose the four probeset-based signatures (NNMT, CH13L1, IGFBP3, TIMP3 and COL1A2) were overexpressed in GHE, as were overexpressed in primary Gbs compared with low-grade gliomas (Tso et al, 2006). The highest prediction accuracy for subtype membership was obtained by our LocSBE (83.5%), while the other ones were far below in performance (61.5% and 68.3% for LeeSBE and ColSBE signatures, respectively). However, the groups distinguished by LocSBE did not show a significant survival difference, whereas the LeeSBE and ColSBE did (Figure 2C and Figures 3A–C). At this point, we hypothesised that a consensus signature (ConsSBE) that included the 12 probesets from the three four probeset-based signatures could improve both the prediction accuracy and the detection of a difference in survival, but such hypothesis failed (Figure 2C).

Figure 3
figure 3

Survival analysis and genetic alterations plots. (A–C) These figures depict survival plots using Lee’s data set and splitting cases using LocSBE, LeeSBE and ColSBE, respectively. (D) We provide the percentage of cases harbouring both IDH1 mutation and non-amplification of EGFR in each Gb subtype (GLE and GHE). (E–G) These figures depict the same than figures (A–C), but using Gravendeel’s data set.

Full size image

Prediction ability on an independent data set

We assigned the class group to cases from Gravendeel’s data set using Equations 1, 2, 3 and evaluated in each Gb group the percentage of individuals simultaneously showing IDH1 mutation and non-amplification of EGFR. Both LocSBE and ColSBE displayed a significantly higher percentage of cases with the mentioned alterations in the GLE group compared with the GHE one (Figure 3D). As previous work reported that secondary Gbs are characterised by a higher accumulation of IDH1 mutation (Yan et al, 2009), the use of LocSBE and ColSBE seems to distinguish these two subtypes. However, only groups identified by ColSBE displayed a differential survival (Figure 3G), whereas LocSBE showed a mild non-significant difference and survival of groups distinguished by LeeSBE was almost identical.

We evaluated the ability of ColSBE as a survival predictor by fitting a proportional hazards Cox’s model (Table 1). We confirmed that those individuals from GHE have almost three times (or 277%) higher probability of death (hazard ratio) than those ones from GLE using Gravendeel’s data set, while higher than two using Lee’s data set. Similarly, the hazard ratio increased almost three times (or 275%) for those patients not displaying IDH1 mutation and almost halved (down to 55.8%) for those ones showing EGFR amplification. Patients simultaneously harbouring IDH1 mutation and EGFR non-amplification further reduced the probability of death down to a 25.5%. In front of this result, we tested whether those patients simultaneously harbouring IDH1 mutation, non-amplification of EGFR and classified as GLE by ColSBE displayed a lower probability of death than the rest of patients. This resulted into a decrease down to 16.1% of the death hazard ratio, or inversely, more than six-fold increase of the death hazard ratio for those patients not showing the above-mentioned pattern for these three features. Cox’s models on Lee’s data set showed that non-proneural cases have an 84.1% higher probability of death than proneural ones. Also, the increase of one KPS unit and radiotherapy administration resulted into a decrease in the hazard ratio down to 95.1% and 50.1%, respectively. On the contrary, each additional year of patient’s life provokes a 2.3% increase of probability of death in Gravendeel’s data set and almost the same percentage (2.5%) in Lee’s data set. None of the rest of variables was a significant predictor of survival.

Table 1 Summary of Cox models
Full size table

On the other hand, considering that probesets composing ColSBE may have a potential diagnostic use, we validated their expression in our local data set samples by RT–PCR. As we shown in Table 2, fold changes between GLE and GHE were coherent with the ones obtained using microarray data.

Table 2 Validation of microarray measurements using RT-PCR
Full size table

Composition of Gb groups

A complementary study of Cox’s models was performed by analysing the composition of GHE and GLE in terms of available variables in Lee’s and Gravendeel’s data sets. We evaluated the percentage of cases from each profile (proneural, proliferative, mixed proliferative-mesenchymal -promes- and mesenchymal) within GHE and GLE. As we shown in Supplementary Figure 1, a significant difference between GHE and GLE is observed, regardless of the equation used to classify cases. However, almost all GLE cases (10 out of 11) belonged to the proneural profile when using ColSBE, while all profiles were represented using LocSBE and only proliferative and promes using LeeSBE. This feature and the increased number of cases with low expression of gene MGMT and VEGF (Supplementary Figure 2) further corroborates that cases classified as GLE by ColSBE are expected to develop a less malignant cancer. In this sense, most patients previously untreated or non-complementarily treated with temodar were classified as GLE (Supplementary Figure 3) by LeeSBE and ColSBE, but this difference was not significant. Gender did not appear to display a different representation between GHE and GLE, but a significant decrease of patient’s age was observed in GLE cases regardless the equation used (Supplementary Figure 4). The validity of results based on ColSBE is also assessed by the statistically equal distribution of collection centres in GHE and GLE, which is not observed using the LocSBE and LeeSBE (Supplementary Figure 1).

Gravendeel’s data set allowed assessing the relevance of loss of heterozygosis of chromosomes 1p and 19q, but not significant difference was observed (Supplementary Figure 5). Inversely, the separated analysis of IDH1 status and EGFR amplification provided an equivalent result than considering simultaneous alterations (Figure 3 and Supplementary Figure 5). Type of surgical resection, radiotherapy and chemotherapy administered did not display a significant percentage difference between GHE and GLE, except the high percentage of patients subjected to chemotherapy in GLE when using the LocSBE (Supplementary Figure 6). The average age of patients was lower in GLE only when the classification was based on ColSBE (Supplementary Figure 7), which confirms the result observed using Lee’s data set. Nevertheless, neither gender, nor KPS appeared to be a differential feature between GHE and GLE.

Discussion

Extensive previous work has tried to uncover a molecular signature, which can be used to improve diagnosis and prognosis of high-grade gliomas and/or specifically Gbs. However, there is no widely accepted and validated consensus equation yet to carry out this discrimination for Gbs. For this reason, we followed a step-wise approach in this work to generate discriminant equations. Our local signature splits cases in two groups (GHE and GLE), which agrees with the number of Gb groups found in Lee’s and Colman’s works. Among genes overexpressed found by Tso and collaborators in primary Gbs compared with low-grade gliomas, only EGFR and SEC61G were not overexpressed in our GHE compared with GLE group. In fact, the lack of overexpression of EGFR and SEC61G in GHE could imply that these two genes are a characteristic feature of Gbs in general, but not a differential feature of primary Gbs. In this sense, the high expression of ADM and FCGBP also shows that these genes could also be characteristic of primary Gbs, although Tso and collaborators found overexpression for both Gb subtypes.

Furthermore, the average age of patients in the GLE group was lower than in GHE when evaluated on Lee’s data set. Both molecular features and age of patients in each group seem to agree with the results published by Tso et al (2006), which described these features for primary and secondary Gbs. Thus, we may hypothesise that GHE and GLE detected using our local signature could correspond to primary and secondary Gbs, respectively. Such hypothesis was confirmed when we applied the equations generated on the fully independent data set made available by Gravendeel and collaborators. The GLE assigned by LocSBE and ColSBE displayed a significant higher percentage of Gbs harbouring both IDH1 mutation and non-amplification of EGFR than GHE. However, only ColSBE was able to distinguish two groups displaying a significant survival difference.

In fact, the percentage of cases showing IDH1 mutation in primary Gbs described by Yan and collaborators (6%) was similar to the percentage of GHE cases detected by ColSBE in Gravendeel’s data set, which displayed both IDH1 mutation and non-amplification of EGFR (6.5%). This value is also similar to the percentage of primary Gbs showing IDH1 mutation, as described by Lai and collaborators. Thus, these features would agree with what had already been described for primary Gbs (Yan et al, 2009; Lai et al, 2011). Moreover, the percentage of cases showing such alteration in GLE cases (44.4%) approached the percentage of proneural cases with IDH1 mutated (30%), as described by Verhaak et al (2010). Considering that only proneural and neural cases showed IDH1 mutation in their work and that GLE based on ColSBE showed a predominant percentage of proneural cases, GLE-classified cases are expected to display a better prognosis than GHE ones. This hypothesis is also confirmed by the significant higher percentage of GLE cases showing low expression of genes MGMT and VEGF, although the expression status of these genes did not imply a significant improvement of survival (Table 1).

In addition, ColSBE-based classification and IDH1/EGFR status are predictors of survival as revealed by Cox models, but stratification of patients by combining ColSBE and IDH1/EGFR status was translated into the strongest decrease of death hazard ratio among variables analysed. This result indicates that these three molecular features do not exclude each other, but provide a refined prediction of patient’s survival. In this sense, our and previous work’s results suggest that an effort should be done to establish a ‘gold-standard’ to classify newly acquired Gb biopsy cases. Our proposed discriminant equation, together with IDH1/EGFR status, provides a link between classical ‘primary’ and ‘secondary’ accumulated clinical information and an objective molecular discrimination of those clinical entities.

Conversely, the high prediction accuracies obtained through LOOCV suggest that in small data sets, class prediction may be fairly optimal, regardless of the signature used. Nevertheless, the prediction of Lee’s cases through a four probeset-based LDA equation revealed a much higher prediction accuracy of our LocSBE (83.5%), as compared with the other ones (61.5 and 68.3%). Comparing these results with the ones obtained from survival analysis, it seems evident that our feature selection method tends to select probesets more able to predict the class group of test cases, rather than detecting differential survival between Gb groups. This can be due to our feature selection strategy that did not consider probesets highly correlated with survival, which is a similar strategy to the one used by Li et al (2009). In contrast, signatures obtained in Lee’s and Colman’s works considered such correlation.

Then, our study proposes a strategy towards the establishment of a ‘gold-standard’ for Gb subtyping. To our knowledge, there is not a single equation available in the literature to directly predict survival or subtype of Gb cases. Then, we have herewith produced formulas (Equation 1, 2, 3) for each gene signature and fully documented the postprocessing protocol for anyone to be able to test their performance. Colman signature-based equation appears to confidently distinguish Gbs with expected high survival and it may differentiate the subtype of Gbs better than the clinical history alone. That is, the classification of primary and secondary Gbs only based in the recurrence of the glioma may be misleading, because early clinical signs or symptoms may have been bypassed. This would artefactually increase the primary Gb group based in clinical history alone. Considering that confident identification of primary/secondary Gb would have a diagnostic interest, but there is no confident method for such a purpose (Ohgaki and Kleihues, 2007; Louis et al, 2007), we propose ColSBE as a diagnostic tool to be tested in the day-to-day work at the (molecular) histopathology laboratory, which used conjointly with evaluation of IDH1/EGFR status may improve prediction of patient’s survival. The validation of expression values from ColSBE through RT–PCR demonstrates the potential diagnostic use of such equation, although we recognise that further work is necessary to fit an LDA equation solely based on RT–PCR values.