Abstract
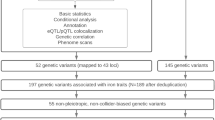
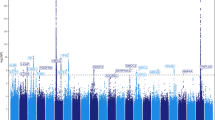
Restless legs syndrome (RLS) is a common multifactorial disease. Some genetic risk factors have been identified. RLS susceptibility also has been related to iron. We therefore asked whether known iron-related genes are candidates for association with RLS and, vice versa, whether known RLS-associated loci influence iron parameters in serum. RLS/control samples (n=954/1814 in the discovery step, 735/736 in replication 1, and 736/735 in replication 2) were tested for association with SNPs located within 4 Mb intervals surrounding each gene from a list of 111 iron-related genes using a discovery threshold of P=5 × 10−4. Two population cohorts (KORA F3 and F4 with together n=3447) were tested for association of six known RLS loci with iron, ferritin, transferrin, transferrin-saturation, and soluble transferrin receptor. Results were negative. None of the candidate SNPs at the iron-related gene loci was confirmed significantly. An intronic SNP, rs2576036, of KATNAL2 at 18q21.1 was significant in the first (P=0.00085) but not in the second replication step (joint nominal P-value=0.044). Especially, rs1800652 (C282Y) in the HFE gene did not associate with RLS. Moreover, SNPs at the known RLS loci did not significantly affect serum iron parameters in the KORA cohorts. In conclusion, the correlation between RLS and iron parameters in serum may be weaker than assumed. Moreover, in a general power analysis, we show that genetic effects are diluted if they are transmitted via an intermediate trait to an end-phenotype. Sample size formulas are provided for small effect sizes.
Similar content being viewed by others
Log in or create a free account to read this content
Gain free access to this article, as well as selected content from this journal and more on nature.com
or
References
Trenkwalder C, Paulus W : Restless legs syndrome: pathophysiology, clinical presentation and management. Nat Rev Neurol 2010; 6: 337–346.
Berger K, von Eckardstein A, Trenkwalder C et al. Iron metabolism and the risk of restless legs syndrome in an elderly general population - the MEMO-Study. J Neurol 2002; 249: 1195–1199.
Högl B, Kiechl S, Willeit J et al. Restless legs syndrome: a community-based study of prevalence, severity, and risk factors. Neurology 2005; 64: 1920–1924.
Pantaleo NP, Hening WA, Allen RP, Earley CJ : Pregnancy accounts for most of the gender difference in prevalence of familial RLS. Sleep Med 2010; 11: 310–313.
Winkelmann J, Schormair B, Lichtner P et al. Genome-wide association study of restless legs syndrome identifies common variants in three genomic regions. Nat Genet 2007; 39: 1000–1006.
Stefansson H, Rye DB, Hicks A et al. A genetic risk factor for periodic limb movements in sleep. N Engl J Med 2007; 357: 639–647.
Schormair B, Kemlink D, Roeske D et al. PTPRD (protein tyrosine phosphatase receptor type delta) is associated with restless legs syndrome. Nat Genet 2008; 40: 946–948.
Vilarino-Guell C, Farrer MJ, Lin SC : A genetic risk factor for periodic limb movements in sleep. N Engl J Med 2008; 358: 425–427.
Kemlink D, Polo O, Frauscher B et al. Replication of estless legs syndrome loci in three European populations. J Med Genet 2009; 46: 315–318.
Winkelmann J, Czamara D, Schormair B et al. Genome-wide association study identifies novel restless legs syndrome susceptibility loci on 2p14 and 16q12.1. PLoS Genet 2011; 7: e1002171.
O'Keeffe ST, Gavin K, Lavan JN : Iron status and restless legs syndrome in the elderly. Age Ageing 1994; 23: 200–203.
Allen RP, Earley CJ : The role of iron in restless legs syndrome. Mov Disord 2007; 22: S440–S448.
Allen RP, Picchietti D, Hening WA et al. Restless legs syndrome: diagnostic criteria, special considerations, and epidemiology. A report from the restless legs syndrome diagnosis and epidemiology workshop at the National Institutes of Health. Sleep Med 2003; 4: 101–119.
Wichmann HE, Gieger C, Illig T : KORA-gen - resource for population genetics, controls and a broad spectrum of disease phenotypes. Gesundheitswesen 2005; 67 (Suppl 1): S26–S30.
Oexle K, Ried JS, Hicks AA et al. Novel association to the proprotein convertase PCSK7 gene locus revealed by analysing soluble transferrin receptor (sTfR) levels. Hum Mol Genet 2011; 20: 1042–1047.
Purcell S, Neale B, Todd-Brown K et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet 2007; 81: 559–575.
Constantine CC, Gurrin LC, McLaren CE et al. SNP selection for genes of iron metabolism in a study of genetic modifiers of hemochromatosis. BMC Med Genet 2008; 9: 18.
Hentze MW, Muckenthaler MU, Galy B, Camaschella C : Two to tango: regulation of Mammalian iron metabolism. Cell 2010; 142: 24–38.
Marchini J, Howie B, Myers S et al. A new multipoint method for genome-wide association studies by imputation of genotypes. Nat Genet 2007; 39: 906–913.
Whitfield JB, Cullen LM, Jazwinska EC et al. Effects of HFE C282Y and H63D polymorphisms and polygenic background on iron stores in a large community sample of twins. Am J Hum Genet 2000; 66: 1246–1258.
Catoire H, Dion PA, Xiong L et al. Restless legs syndrome-associated MEIS1 risk variant influences iron homeostasis. Ann Neurol 2011; 70: 170–175.
Sun ER, Chen CA, Ho G et al. Iron and restless legs syndrome. Sleep 1998; 21: 381–387.
Frauscher B, Gschliesser V, Brandauer E et al. The severity range of restless legs syndrome (RLS) and augmentation in a prospective patient cohort: association with ferritin levels. Sleep Med 2009; 10: 611–615.
Trenkwalder C, Högl B, Benes H, Kohnen R : Augmentation in restless legs syndrome is associated with low ferritin. Sleep Med 2008; 9: 572–574.
Curgunlu A, Döventaş A, Karadeniz D et al. Prevalence and characteristics of restless legs syndrome (RLS) in the elderly and the relation of serum ferritin levels with disease severity: Hospital-based study from Istanbul, Turkey. Arch Gerontol Geriatr 2012; 55: 73–76.
Quinn C, Uzbeck M, Saleem I et al. Iron status and chronic kidney disease predict restless legs syndrome in an older hospital population. Sleep Med 2011; 12: 295–301.
Kim KW, Yoon IY, Chung S et al. Prevalence, comorbidities and risk factors of restless legs syndrome in the Korean elderly population - results from the Korean Longitudinal Study on Health and Aging. J Sleep Res 2010; 19: 87–92.
Oexle K : A remark on rare variants. J Hum Genet 2010; 55: 219–226.
Pe'er I, Yelensky R, Altshuler D, Daly MJ : Estimation of the multiple testing burden for genomewide association studies of nearly all common variants. Genet Epidemiol 2008; 32: 381–385.
Sokal RR, Rohlf FJ : Biometry. New York: WH Freeman and Company, 1995, p 578.
Hsieh FY, Bloch DA, Larsen MD : A simple method of sample size calculation for linear and logistic regression. Stat Med 1998; 17: 1623–1634.
Bull SB : Sample size and power determination for a binary outcome and an ordinal exposure when logistic regression analysis is planned. Am J Epidemiol 1993; 137: 676–684.
Demidenko E : Sample size determination for logistic regression revisited. Stat Med 2007; 26: 3385–3397.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies the paper on European Journal of Human Genetics website
Supplementary information
Appendix
Appendix
For small effect sizes, the test statistics of linear and logistic regression analyses approximate standard normal distributions. Small effect sizes also imply that the variances under the alternative and the null hypothesis are approximately equal. The formulas in power calculations of necessary sample size n therefore simplify to

where t is the test statistic and Zα/2 and Zβ are quantiles of a standard normal distribution that correspond to the tolerated error rates α and β, that is, to the required significance and power (1−β), respectively.
(1) In the case of linear regression analysis, consider a set of independent individuals where each individual i displays a continuous trait yi that is influenced by an allele of a gene with effect size axy and frequency q. This allele occurs in xi ∈ {0,1,2} copies and is assumed to be in Hardy–Weinberg equilibrium. In the linear model, yi is given as yi=a0+axyxi+ɛi where a0 and axy are constants and ɛi is a noise parameter. The model is scaled so that ɛ has a standard normal distribution with zero mean and unit variance. The precise sample size determination30, 31 yields n=(Zα/2+Zβ)2/C(ρ)2+3 where C(ρ)=½ln((1+ρ)/(1−ρ)) is the Fisher transformation of the correlation coefficient ρ=axyσx/σy. For small axy (ie, small ρ), we can approximate C(ρ) by first-order expansion as C(ρ)≈ρ. Moreover, the variance of the noise term being unity and axy being small, the variance of y is σy2=axy2σx2+1≈1. To calculate ρ we also need σx. In Hardy–Weinberg equilibrium with we get σx2=Σ(xi−μx)2qxi(1−q)(2-xi)=2q(1−q). For small effect axy and, consequently, large sample size (» 3) we thus arrive at

(2) In logistic regression analysis,31, 32, 33 the association between a binary response (eg, disease present or absent) and an exposure variable y is modeled as logit(P(z|y))=log(P(1|y)/P(0|y))=b0+byzy where P(z|y), z ∈ {0,1}, is the conditional response probability, and b0 and byz are constants. The value of the effect parameter byz is estimated by maximum likelihood estimation. For a small effect byz, the variance of the estimator under the alternative hypothesis approximates the variance under the null hypothesis, [P(1−P)σy2]−1, where P is the average response probability with . If y has a standard normal distribution with σy2=1, equation (A1) yields the necessary sample size as

The same derivation applies to multiple logistic regression with logit(P(z|x,ɛ))=c0+cxzx+cɛzɛ+…, if the effects of the variates x, ɛ,… are small. Assuming that x ∈ {0,1,2} represents a genotype distribution in Hardy–Weinberg equilibrium with allele frequency q (implying σx2=2q(1−q), see above), the necessary sample size to estimate the effect size cxz then is

where P is the average response probability with P≈P(0|x=0,ɛ=0)= .
.
Rights and permissions
About this article
Cite this article
Oexle, K., Schormair, B., Ried, J. et al. Dilution of candidates: the case of iron-related genes in restless legs syndrome. Eur J Hum Genet 21, 410–414 (2013). https://doi.org/10.1038/ejhg.2012.193
Received:
Revised:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/ejhg.2012.193
Keywords
This article is cited by
-
Restless legs syndrome/Willis–Ekbom disease prevalence in beta thalassemia patients
Sleep and Breathing (2018)
-
Iron and hepcidin as risk factors in atherosclerosis: what do the genes say?
BMC Genetics (2015)
-
Neuroimaging, nutrition, and iron-related genes
Cellular and Molecular Life Sciences (2013)