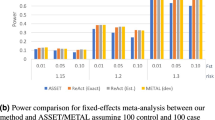
Abstract
Current genome-wide association studies (GWAS) focusing on relatively common single-nucleotide polymorphisms (SNPs) usually adopt a cost-effective multi-staged design in which a proportion of the total samples are genotyped using a commercial SNP array with a reasonably good coverage of the whole genome at the initial stage, and a list of promising SNPs are further genotyped and evaluated on the remaining samples at the second stage. This staged design in principal can also be used for the study of rare genetic variants at the genome-wide scale, but the statistical methods developed for evaluating the relatively common SNPs under the staged design are not appropriate for rare variants due to the invalidity of large sample theorems. Here, we develop a new statistical framework that aims to evaluate rare variants under two-staged (or multi-staged) design. By extensive computer simulations, we evaluate the empirical type I error rate and power of the proposed procedures. A real example from two recent case–control rheumatoid arthritis genetic association studies is also used to demonstrate the performances of the proposed methods.
Similar content being viewed by others
Log in or create a free account to read this content
Gain free access to this article, as well as selected content from this journal and more on nature.com
or
References
Pritchard, J. K. Are rare variants responsible for susceptibility to complex diseases? Am. J. Hum. Genet. 69, 124–137 (2001).
Cohen, J. C., Kiss, R. S., Pertsemlidis, A., Marcel, Y. L., McPherson, R. & Hobbs, H. H. Multiple rare alleles contribute to low plasma levels of HDL cholesterol. Science 305, 869–872 (2004).
Fearnhead, N. S., Wilding, J. L., Winney, B., Tonks, S., Bartlett, S., Bicknell, D. C. et al Multiple rare variants in different genes account for multifactorial inherited susceptibility to colorectal adenomas. Proc. Natl Acad. Sci. USA 101, 15992–15997 (2004).
Cohen, J. C., Pertsemlidis, A., Fahmi, S., Esmail, S., Vega, G. L., Grundy, S. M. et al Multiple rare variants in NPC1L1 associated with reduced sterol absorption and plasma low-density lipoprotein levels. Proc. Natl Acad. Sci. USA 103, 1810–1815 (2006).
Kryukov, G. V., Pennacchio, L. A. & Sunyaev, S. R. Most rare missense alleles are deleterious in humans: implications for complex disease and association studies. Am. J. Hum. Genet. 80, 727–739 (2007).
Azzopardi, D., Dallosso, A. R., Eliason, K., Hendrickson, B. C., Jones, N., Rawstorne, E. et al Multiple rare nonsynonymous variants in the adenomatous polyposis coli gene predispose to colorectal adenomas. Cancer Res. 68, 358–363 (2008).
Gorlov, I. P., Gorlova, O. Y., Sunyaev, S. R., Spitz, M. R. & Amos, C. I. Shifting paradigm of association studies: value of rare single-nucleotide polymorphisms. Am. J. Hum. Genet. 82, 100–112 (2008).
Ji, W., Foo, J. N., O’Roak, B. J., Zhao, H., Larson, M. G., Simon, D. B. et al Rare independent mutations in renal salt handing genes contribute to blood pressure variation. Nat. Genet. 40, 592–599 (2008).
Slatter, T. L., Jones, G. T., Williams, M. J., Van Rij, A. M. & McCormick, S. P. Novel rare mutations and promoter haplotypes in ABCA1 contribute to low-HDL-C levels. Clin. Genet. 73, 179–184 (2008).
Stefansson, H., Rujescu, D., Cichon, S., Pietiläinen, O. P., Ingason, A., Steinberg, S. et al Large recurrent microdeletions associated with schizophrenia. Nature 455, 232–236 (2008).
Walsh, T., McClellan, J. M., McCarthy, S. E., Addington, A. M., Pierce, S. B., Cooper, G. M. et al Rare structural variants disrupt multiple genes in neurodevelopmental pathways in schizophrenia. Science 320, 539–543 (2008).
Nejentsev, S., Walker, N., Riches, D., Egholm, M. & Todd, J. A. Rare variants of IFIH1, a gene implicated in antiviral responses, protect against type 1 diabetes. Science 324, 387–389 (2009).
Cirulli, E. T. & Goldstein, D. B. Uncovering the roles of rare variants in common disease through whole-genome sequencing. Nat. Rev. Genet. 11, 415–425 (2010).
Dickson, S. P., Wang, K., Krantz, I., Hakonarson, H. & Goldstein, D. B. Rare variants create synthetic genome-wide associations. PLoS Biol. 8, e1000294 (2010).
Mitsui, J., Fukuda, Y., Azuma, K., Tozaki, H., Ishiura, H., Takahashi, Y. et al Multiplexed resequencing analysis to identify rare variants in pooled DNA with barcode indexing using next-generation sequencer. J. Hum. Genet. 55, 448–455 (2010).
Li, B. & Leal, S. M. Methods for detecting associations with rare variants for common disease: application to analysis of sequence data. Am. J. Hum. Genet. 83, 311–321 (2008).
Li, B. & Leal, S. M. Discovery of rare variants via sequencing: implications for the design of complex trait association studies. PLoS Genet. Genetics 5, e1000481 (2009).
Price, A. L., Kryukov, G. V., de Bakker, P. I., Purcell, S. M., Staples, J., Wei, L. J. et al Pooled association tests for rare variants in exon-resequencing studies. Am. J. Hum. Genet. 86, 832–838 (2010).
Morris, A. P. & Zeggini, E. An evaluation of statistical approaches to rare variant analysis in genetic association studies. Genet. Epidemiol. 34, 188–193 (2010).
Ionita-Laza, I., Buxbaum, J. D., Laird, N. M. & Lang, C. A new testing strategy to identify rare variants with either risk or protective effect on disease. PLoS Genet. 7, e1001289 (2011).
Satagopan, J. M. & Elston, R. C. Optimal two-stage genotyping in population-based association studies. Genet. Epidemiol. 25, 149–157 (2003).
Satagopan, J. M., Venkatraman, E. S. & Begg, C. B. Two-stage designs for gene-disease association studies with sample size constraints. Biometrics 60, 589–597 (2004).
Thomas, D., Xie, R. & Gebregziabher, M. Two-stage sampling designs for gene association studies. Genet. Epidemiol. 27, 401–414 (2004).
Skol, A. D., Scott, L. J., Abecasis, G. R. & Boehnke, M. Joint analysis is more efficient than replication-based analysis for two-stage genome-wide association studies. Nat. Genet. 38, 209–213 (2006).
Schaid, D. J. & Sinnwell, J. P. Two-stage case-control designs for rare genetic variants. Hum. Genet. 127, 659–668 (2010).
Pan, D., Li, Q., Jiang, N., Liu, A. & Yu, K. Robust joint analysis allowing for model uncertainty in two-stage genetic association studies. BMC Bioinformatics 12, 9 (2011).
Li, Q., Zhang, H. & Yu, K. Approaches for evaluating rare polymorphisms in genetic association studies. Hum. Hered. 69, 219–228 (2010).
Li, Q., Li, G. & Xiong, S. Assessment of cell number for a multinomial distribution with application to genomic data. Metrika 71, 151–164 (2010).
Silman, A. J. & Pearson, J. E. Epidemiology and genetics of rheumatoid arthritis. Arthritis Res. Ther. 4 ((Suppl 3)) S265–S272 (2002).
MacGregor, A. J., Snieder, H., Rigby, A. S., Koskenvuo, M., Kaprio, J., Aho, K. et al Characterizing the quantitative genetic contribution to rheumatoid arthritis using data from twins. Arthritis Rheum. 43, 30–37 (2000).
Raychaudhuri, S., Remmers, E. F., Lee, A. T., Hackett, R., Guiducci, C., Burtt, N. P. et al Common variants at CD40 and other loci confer risk of rheumatoid arthritis. Nat. Genet. 40, 1216–1223 (2008).
Orozco, G., Hinks, A., Eyre, S., Ke, X., Gibbons, L. J., Bowes, J. et al Combined effects of three independent SNPs greatly increase the risk estimate for RA at 6q23. Hum. Mol. Genet. 18, 2693–2699 (2009).
Bowes, J., Lawrence, R., Eyre, S., Panoutsopoulou, K., Orozco, G., Elliott, K. S. et al Rare variation at the TNFAIP3 locus and susceptibility to rheumatoid arthritis. Hum. Genet. 128, 627–633 (2010).
Stahl, E. A., Raychaudhuri, S., Remmers, E. F., Xie, G., Eyre, S., Thomson, B. P. et al Genome-wide association study meta-analysis identifies seven new rheumatoid arthritis loci. Nat. Genet. 42, 508–514 (2010).
Acknowledgements
We would like to thank two anonymous referees for their insightful comments. This work was partially supported by the National Science Foundation of China (10901155, 61134013 to Q.L.).
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
A.1 Lemma
Suppose that X follows a binomial distribution with parameters n and θ. Then for any given α∈(0,1),
Proof. For 
define
Let 
. Define 
.
According to Lemma 1 of Li, Li, & Xiong (2010),28 
So, V(kα,1)=α−o(1), and v(kα,2)=α−o(1). We now consider two cases:
(1) When 
,
(2) When 
, in the similar way, we have the results.
A.2 Derivation of the Threshold for the Joint Testing Statistic
To controll the type I error rate of the joint analysis, we have
Based on the Lemma above, when min(r,s) →∞ and r/s 
, we can get 
means ‘convergence in distribution’ and U(0,1) is the standard uniform distribution. Now, we calculate the threshold c from the above equation under the following two scenarios:
(1) When 
. Then X and Y are independent with the probability density functions 
, respectively. So the joint probability density function of (X,Y)′ is
Then, we calculate
Therefore g(c) is a strictly increasing function on the interval 
. Then the equation g(c)=α has a unique solution of c on 
because of g(−∞)=0 and 
. So, we can use the Bi-section Method to get c.
(2) When π=0.5,
As 
, no solution exists.
And when 
, we have
so the threshold c is the solution of the equation 
. Let 
. Note that 
. So, h(c) is strictly increasing as 
. As 
, h(−∞)=0, 
has a unique solution on 
.
Rights and permissions
About this article
Cite this article
Li, Q., Pan, D., Yue, W. et al. Evaluating rare variants under two-stage design. J Hum Genet 57, 352–357 (2012). https://doi.org/10.1038/jhg.2012.33
Received:
Revised:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/jhg.2012.33
