Introduction

Single photons and single photon qubits are among the foundations of most quantum optical information processing techniques such as cryptography,1 teleportation,2 repeaters3 and computing.4 Many of these applications require the photons to have a well-defined, pure modal structure. Possessing precise information about that structure is essential for quantum optical technology.

An approximate guess of a photon's mode can be inferred theoretically from the characteristics of the source,5,6,7,8,9 but this information is not always available or reliable. For example, this approach would not work for photons sent in by a remote party in a communication scheme, or for photons from an incompletely characterized mesoscopic source. Therefore, it is important to have a technique for precise characterization of a photon's mode experimentally. While such techniques are relatively well developed for spatial modes,10,11 their extension into the temporal domain is challenging.

One approach to studying the temporal structure of the photon would be to look at the photon detection event statistics as a function of time. For example, this approach has been used to study the timing of coherent double Raman scattering from an atomic ensemble.12 Further insight into the photon preparation quality can be gained by studying time-dependent photon counting autocorrelation statistics.13 However, these techniques provide no information about the phase coherence between different segments of the photon's temporal mode.

Complete information about a photon's temporal properties can be obtained by studying its interference with a classical field. Polycarpou et al. used adaptive waveform shaping of local oscillator (LO) pulses14 to heuristically find the LO temporal mode that maximizes the efficiency of homodyne detection of the photon. This occurs when the LO temporal mode matches that of the signal, enabling measurement of that mode. However, physical shaping of LO pulses is quite sophisticated experimentally. Furthermore, this technique has only been demonstrated for pure temporal modes.

An alternative approach to measuring the spectral density matrix of the photon has been proposed in Ref.15. It is based on bringing the photon into interference with a pair of weak coherent pulses with varied separation between them. However, this method can only be applied to ultrashort pulses whose width is a few optical cycles. Furthermore, the experimental test in Ref.15 has been performed on a thermal state rather than the single photon state.

For a photon with bandwidth resolvable by detection electronics, the time domain statistics may be measured directly and in real time by analyzing the time-dependent statistics of the homodyne detector's output photocurrent with a continuous-wave LO. MacRae et al. 16,17 showed that the autocorrelation function of this photocurrent estimates the real part of the density matrix defining the photon's temporal mode. Subsequently, this approach has been utilized for the ‘Schrödinger cat’ and two-photon Fock states.18

However, this method does not yield any information about the imaginary part of the photon's temporal density matrix (TDM). In this paper we present an experimental technique of polychromatic optical heterodyne tomography, which relies on acquiring the autocorrelation data of the homodyne photocurrent at multiple LO frequencies. The method enables us to determine both the real and imaginary parts of the photon's TDM, or, equivalently, both its amplitude and phase, thereby completely characterizing its temporal state. It works equally well for pure and mixed temporal modes.

Materials and methods

The (pure) temporal mode of a photon is defined by annihilation operator

where φ(t) is the temporal mode function (TMF) and represents the instantaneous annihilation operator at time t. Although single photons associated with a certain moment in time are ill-defined, treatment (1) is approximately valid as long as the spectral width of the photon is much less than its frequency.19 A single photon state in this mode is then given by , where .

The digital nature of the data acquisition system used in our experiment compels us to represent the temporal modes in terms of discrete time bins. The single photon state in temporal mode φ(t) can then be approximately expressed as with . Here tj is the time associated with the jth bin and is the state containing one photon in the top-hat temporal mode associated with the jth bin and vacuum in all other bins. The density operator of the photon is then represented as where ρmn is the TDM.

The homodyne current for the jth time bin I(tj) is proportional to the quadrature

where θj = δω⋅tj + θ0 is the optical phase difference between the LO and the signal. Here δω is the frequency detuning between the LO and the signal and θ0 the LO relative phase at t = 0. The autocorrelation matrix for the homodyne current is then

where each matrix element can be evaluated using Equation (2) as

Note that Equation (4) does not depend on θ0 due to the phase uncertainty of Fock states.

From Equations (3) and (4), one can obtain

The first term in Equation (5) corresponds to the autocorrelation matrix for the vacuum. The second term, which we call the reduced autocorrelation matrix, is directly related to the photon's TDM:

If the LO frequency is same as that of the signal, i.e., at δω = 0, the autocorrelation matrix depends only on the real part of the TDM. However, by using δω ≠ 0 one obtains access to its imaginary part.

In a realistic experiment, the photon being tested may experience losses, resulting in admixture of the vacuum into the state detected. Our technique would still apply to this case, but the second term would enter Equation (5) with the coefficient equal to the transmissivity of the lossy element. For high losses, acquisition of larger quantities of data may be necessary to reduce the statistical uncertainties (detailed further in the Supplementary Material).

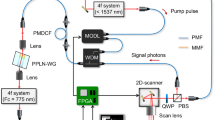
Our experimental scheme for creating the single photon state and measuring the autocorrelation matrix is shown in Figure 1. We use coherent double Raman scattering (four-wave mixing) in an ensemble of Λ-type atoms to generate a two-mode squeezed state in a non-degenerate phase-matched configuration.17 A hot 85Rb vapor cell is pumped by a 1 Watt laser beam at 795 nm derived from a continuous-wave Ti:Sapphire laser. The signal and idler beams are spatially separated from the pump, and a specific spatial mode is selected in the idler channel using a single-mode fiber. Subsequently, the idler channel is subjected to spectral filtering by means of a lens cavity (C1) of a 55 MHz bandwidth20 and a conventional Fabry–Perot cavity (C2) of bandwidth γ/2π = 7 MHz. The usage of two cavities with incommensurate free spectral ranges ensures that the combined spectral filter has a single transmission peak of 7 MHz width. This results in a heralded photon with a temporal mode that can be easily resolved by our homodyne detector with a 100 MHz bandwidth.21

Figure 1.
figure 1

(a) Schematic of the experimental setup. The signal (blue) goes to the homodyne detector, whereas the idler (orange) passes through C1 (55 MHz) and C2 (7 MHz) before detection via the SPCM. The EOM between C1 and C2 is optional. (b) The 85Rb three-level Λ system, with the fields' configuration shown. (c) Reconstruction of the state of the electromagnetic field in the temporal mode determined experimentally (unmodulated case). Left to right: experimental quadrature distribution (blue) overlaid with that for the vacuum state (red); diagonal elements of the Fock-basis density matrix; Wigner function. The single-photon fraction is 52.9%. C1, C2: filter cavities; EOM: electro-optic modulator; SPCM: single photon counting module.

Full size image

The idler beam is then coupled to a PerkinElmer single photon counting module (SPCM) with a dark count rate below 100 Hz. Both cavities are maintained at a stable frequency by using an alignment beam which is unblocked every few seconds to monitor and readjust the cavity resonance frequency. Detection of an idler photon projects the signal onto a single photon in a well-defined spatiotemporal mode conjugate to the idler. This signal channel is mode-matched with a continuous-wave LO (18 mW) for homodyne detection.21 The LO is derived from a diode laser that is locked and phase stabilized with respect to the pump using an optical phase-lock loop.22

A click from the SPCM in the idler channel acts as the trigger for the measurement of the signal. The homodyne photocurrent is recorded for 360 ns around the trigger point as reference with a time binning of 2 ns. For each LO detuning, the autocorrelation matrix (3) of the homodyne photocurrent is obtained by taking an average over 2 million traces.

Theoretically, the data corresponding to two LO detunings would constitute a quorum for the temporal mode reconstruction. Experimentally, however, we take data at eight different detunings to avoid the situation where the sinusoids in Equation (6) approach zero for all detunings simultaneously and to enhance the statistical accuracy of the recovered .

Once the autocorrelation matrices have been acquired, we process them to eliminate the vacuum term in Equation (5), as well as any contributions from the DC (direct current) bias in the homodyne photocurrent and thermal background. These contributions are not correlated with trigger events, and are only dependent on the difference tj − tk. They can therefore be evaluated as the mean autocorrelation value along lines tj − tk = const for the data points acquired significantly after the trigger pulse where no signal photon is expected. Subtracting them from the autocorrelation matrix yields the reduced autocorrelation matrix (Figure 2) (detailed further in the Supplementary Material).

Figure 2.
figure 2

Theoretical (right) and experimental (left) reduced autocorrelation matrices, for two different local oscillator detunings: (a) 0 MHz and (b) 27 MHz, corresponding to the measurement setting without modulation. The trigger photon arrives at t = 155 ns.

Full size image

The TDM can now be determined by solving Equation (6) for each pair (j, k). However, such direct approach does not ensure positivity and normalization of the reconstructed density operator. To incorporate these a priori constraints into the reconstruction, we implement a more sophisticated iterative optimization algorithm. The algorithm uses the eight experimental reduced autocorrelation matrices as the training set. The difference between the experimental left-hand side of Equation (6) and the right-hand side of that equation evaluated from the estimated TDM, squared and summed over all pairs (j, k) and all LO frequencies, is used as the cost function. Iterations utilize the diagonal representation of the TDM: . In the first step of each iteration, the eigenvalues pi are adjusted to minimize the cost function while keeping them real, non-negative and totalling 1. In the second step, the eigenvectors are optimized by pairwise unitary transformations. The process is repeated until the cost function asymptotically converges to give the best fit of the TDM.

The theoretically expected mode is calculated from the properties of our experimental setup. The primary element determining the mode of the heralded photon is the narrowband filter cavity C2 in the idler channel. Additionally, the mode's bandwidth is limited by the ∼50 MHz gain bandwidth of the four-wave mixing process used to generate the biphotons. This effect is taken into account in theoretical plots in Figures 2 and 3, however we neglect it in the theoretical expressions below for clarity.

Figure 3.
figure 3

Experimentally reconstructed temporal modes and their theoretical predictions for the cases without modulation (a), with virtual phase modulation (b), and with phase-randomized EOM modulation (c). For each case, the first and second panels show the real (first) and imaginary (second) parts of the TDM, with the insets showing corresponding theoretical plots. The third and fourth panels show the TDM's primary eigenvector as reconstructed from experimental data (solid red) and theoretical modeling (dashed blue). The green dotted line in (c) also shows the diagonal of the TDM, which is not affected by the modulation as expected from Equation (10). The insets in the third panels show the distribution of eigenvalues (red bars) obtained experimentally. Without EOM modulation (a, b), the theoretically expected mode is pure so the TDM is expected to have only one nonvanishing eigenvector. In the case with EOM modulation (c), the TDM is mixed and the solid blue dots in the inset show theoretical eigenvalues. The trigger photon arrives at t = 155 ns for (a), (b) and at t = 145 ns for (c). EOM, electro-optic modulator; TDM, temporal density matrix.

Full size image

The Lorentzian filter C2 in the idler channel produces a signal photon with the TMF in the shape of a rising exponential that terminates at the trigger event (detailed further in the Supplementary Material):

where Θ(t) is the Heaviside step function and γ = 2π × 7 MHz is the narrowband cavity linewidth. This exponentially rising mode is of particular significance for applications such as high-efficiency excitation of an atom23,24 or a resonator25,26 with a single photon. To our knowledge, this is the first demonstration of complete reconstruction of this mode.

Results and discussion

Figure 3a shows the TDM obtained by iterative reconstruction from the experimental data along with the theoretical predictions. The primary eigenvector of the TDM has a corresponding eigenvalue almost 45 times larger than the second largest one indicating a nearly pure temporal mode. The TDM is primarily real and matches well the theoretical prediction.

Next, we demonstrate the reconstruction of a temporal mode with a nonvanishing imaginary component. To this end, we induce a virtual frequency shift by redefining the signal-LO detuning according to δω′ = δω + Δ when reconstructing the TDM from Equation (6). The theoretically expected TMF and TDM then become:

The TDM reconstructed from the experimental data using the effective modulation frequency of Δ = 2π × 5 MHz is shown in Figure 3b. While the purity of the temporal mode is maintained, the reconstructed density matrix now has a significant imaginary component, demonstrating the ability of our technique to accurately reconstruct states with complex temporal modes.

This example is practically relevant in a situation when one does not know the frequency of the photon precisely. In this case, heterodyne measurements at different LO detunings relative to a given reference (defined by the point δω = 0) will provide full information about the mode, including the spectral offset of the photon with respect to that reference.

Finally, we illustrate the ability of our experimental technique to reconstruct the TDM in the case of a mixed state. We phase modulate the signal photons at a frequency ωm = 2π × 20 MHz, larger than the spectral width of C2. This is achieved by passing the idler photons through an electro-optic modulator (EOM), with its optical axis oriented along the photon's polarization.27 This leads to a TMF φEOM(t, θm)=Θ(−t), where β = 1.1 is the modulation index and θm is the phase of the modulating voltage at the time when the idler photon is detected. Because the idler photon detections occur at random times, θm is randomized, leading to the following non-pure TDM:

where J0 is the Bessel function of the first kind.

The experimentally reconstructed TDM is shown in Figure 3c. The mixed nature of the density matrix is evident from the distribution of eigenvalues, with the ratio of the first and second eigenvalues being only around 2. Due to the modulation phase randomization, the imaginary part of the density matrix is zero.

The observed artifacts in the reconstructed photon modes can be attributed to the finite bandwidth, or non-instantaneous response, of the homodyne detector. This results in the smearing of the acquired autocorrelation matrix. This effect is particularly significant where this matrix has sharp features, such as the trigger event where the photon pulse instantly terminates according to Equation (7), as seen in Figure 3a and 3b. The fast modulation of the TMF such as in Figure 3c has a similar effect on the reconstructed mode over its entire duration, resulting in a spurious nonzero imaginary part. The observed artifacts, however, do not significantly degrade the fidelities of the experimentally obtained TDMs with respect to the theoretically expected ones. These fidelities, defined as with the subscripts indicating theory versus experiment, are found to be 0.97, 0.94, and 0.93, respectively, for the three cases of Figure 3.

Using the absolute value of the TMF obtained for the primary mode of the unmodulated case (Figure 3a), we reconstruct the quantum state of light in that mode in the Fock basis akin to Ref.17, obtaining the single photon efficiency of ρ11 = 52.9%. The corresponding Wigner function, exhibiting negative values at the phase-space origin, is plotted in Figure 1c along with the acquired quadrature distribution and the reconstructed density matrix.

Conclusion

We have developed and experimentally demonstrated polychromatic optical heterodyne tomography, a robust method for complete experimental determination of the temporal properties of a single photon directly from the time-resolved photocurrent statistics of a balanced homodyne measurement. The method enables the extraction of a temporal mode which in general may be complex and can have multiple frequency components. Accurate detection of the temporal mode is key for the proper mode matching required by many quantum communication protocols.

Our method permits straightforward extension to states other than the single photon Fock state akin to Ref.18 provided that the state in question occupies a well-defined spatiotemporal mode. On the other hand, the single photon state is special in that it can be directly associated with the photon annihilation operator of a certain optical mode or a mixture thereof. The problem of defining the optical mode(s) for a general quantum optical state is a subject of a separate study.

Although the technique described in this work requires the frequency spectrum of the photon's temporal mode to be sufficiently narrowband so its temporal structure can be resolved by the homodyne detector, one can envision ways to lift this restriction. For example, if the photon is produced in an ultrashort pulsed mode, one can extend it in time using a dispersive element such as an optical fiber, and perform time-resolved homodyne detection using a matched chirped LO. The time-domain correlations of the homodyne photocurrent will then correspond to quantum coherences between components of the photon spectrum.