Abstract
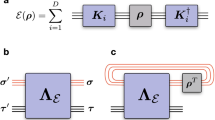
Measurement connects the world of quantum phenomena to the world of classical events. It has both a passive role—in observing quantum systems—and an active one, in preparing quantum states and controlling them. In view of the central status of measurement in quantum mechanics, it is surprising that there is no general recipe for designing a detector that measures a given observable1. Compounding this, the characterization of existing detectors is typically based on partial calibrations or elaborate models. Thus, experimental specification (that is, tomography) of a detector is of fundamental and practical importance. Here, we present the realization of quantum detector tomography2,3,4. We identify the positive-operator-valued measure describing the detector, with no ancillary assumptions. This result completes the triad, state5,6,7,8,9,10,11, process12,13,14,15,16,17 and detector tomography, required to fully specify an experiment. We characterize an avalanche photodiode and a photon-number-resolving detector capable of detecting up to eight photons18. This creates a new set of tools for accurately detecting and preparing non-classical light.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Similar content being viewed by others
References
Braginsky, V. R. & Khalili, F. Ya. Quantum Measurement 38 (Cambridge Univ. Press, 1992).
Luis, A. & Sanchez-Soto, L. L. Complete characterization of arbitrary quantum measurement processes. Phys. Rev. Lett. 83, 3573–3576 (1999).
Fiurasek, J. Maximum-likelihood estimation of quantum measurement. Phys. Rev. A 64, 024102 (2001).
D’Ariano, G. M., Maccone, L. & Lo Presti, P. Quantum calibration of measurement instrumentation. Phys. Rev. Lett. 93, 250407 (2004).
Vogel, K. & Risken, H. Determination of quasiprobability distributions in terms of probability distributions for the rotated quadrature phase. Phys. Rev. A 40, 2847–2849 (1989).
Smithey, D. T., Beck, M., Raymer, M. G. & Faridani, A. Measurement of the Wigner distribution and the density matrix of a light mode using optical homodyne tomography: Application to squeezed states and the vacuum. Phys. Rev. Lett. 70, 1244–1247 (1993).
Banaszek, K., Radzewicz, C., Wodkiewicz, K. & Krasinski, J. S. Direct measurement of the Wigner function by photon counting. Phys. Rev. A 60, 674–677 (1999).
Banaszek, K., D’Ariano, G. M., Paris, M. G. A. & Sacchi, M. F. Maximum-likelihood estimation of the density matrix. Phys. Rev. A 61, 010304(R) (2000).
White, A. G., James, D. F. V., Munro, W. J. & Kwiat, P. G. Exploring Hilbert space: Accurate characterization of quantum information. Phys. Rev. A 65, 012301 (2002).
Ourjoumtsev, A., Jeong, H., Tualle-Brouri, R. & Grangier, P. Generation of optical ‘Schrödinger cats’ from photon number states. Nature 448, 784–786 (2007).
Neergaard-Nielsen, J. S., Melholt Nielsen, B., Hettich, C., Mølmer, K. & Polzik, E. S. Generation of a superposition of odd photon number states for quantum information networks. Phys. Rev. Lett. 97, 083604 (2006).
Chuang, I. L. & Nielsen, M. A. Prescription for experimental determination of the dynamics of a quantum black box. J. Mod. Opt. 44, 2455–2467 (1997).
Poyatos, J. F., Cirac, J. I. & Zoller, P. Complete characterization of a quantum process: The two-bit quantum gate. Phys. Rev. Lett. 78, 390–393 (1997).
Altepeter, J. B. et al. Ancilla-assisted quantum process tomography. Phys. Rev. Lett. 90, 193601 (2003).
D’Ariano, G. M. & Maccone, L. Measuring quantum optical Hamiltonians. Phys. Rev. Lett. 80, 5465–5468 (1998).
Nielsen, M. A., Knill, E. & Laflamme, R. Complete quantum teleportation using nuclear magnetic resonance. Nature 396, 52–55 (1998).
Mitchell, M. W., Ellenor, C. W., Schneider, S. & Steinberg, A. M. Diagnosis, prescription and prognosis of a Bell-state filter by quantum process tomography. Phys. Rev. Lett. 91, 120402 (2003).
Achilles, D., Silberhorn, Ch., Sliwa, C., Banaszek, K. & Walmsley, I. A. Fiber-assisted detection with photon number resolution. Opt. Lett. 28, 2387–2389 (2003).
Resch, K. J. et al. Time-reversal and super-resolving phase measurements. Phys. Rev. Lett. 98, 223601 (2007).
Higgins, B. L., Berry, D. W., Bartlett, S. D., Wiseman, H. M. & Pryde, G. J. Entanglement-free Heisenberg-limited phase estimation. Nature 450, 393–396 (2007).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Dunn, T., Walmsley, I. A. & Mukamel, S. Experimental determination of the quantum-mechanical state of a molecular vibrational mode using fluorescence tomography. Phys. Rev. Lett. 74, 884–887 (1995).
O’Brien, J. L. et al. Quantum process tomography of a controlled-NOT gate. Phys. Rev. Lett. 90, 193601 (2004).
Lvovsky, A. I. et al. Quantum state reconstruction of the single-photon Fock state. Phys. Rev. Lett. 87, 050402 (2001).
Boyd, S. & Vandenberghe, L. Convex Optimization (Cambridge Univ. Press, 2004).
Achilles, D. et al. Photon-number-resolving detection using time-multiplexing. J. Mod. Opt. 51, 1499–1515 (2004).
Eisert, J., Scheel, S. & Plenio, M. B. Distilling Gaussian states with Gaussian operations is impossible. Phys. Rev. Lett. 89, 137903 (2002).
Browne, D. E., Eisert, J., Scheel, S. & Plenio, M. B. Driving non-Gaussian to Gaussian states with linear optics. Phys. Rev. A 67, 062320 (2003).
Kardynal, B. E., Yuan, Z. L. & Shields, A. J. An avalanche-photodiode-based photon-number-resolving detector. Nature Photon. 2, 425–428 (2008).
Boulant, N., Havel, T. F., Pravia, M. A. & Cory, D. G. Robust method for estimating the Lindblad operators of a dissipative quantum process from measurements of the density operator at multiple time points. Phys. Rev. A 67, 042322 (2003).
Jezek, M., Fiurasek, J. & Hradil, Z. Quantum inference of states and processes. Phys. Rev. A 68, 012305 (2003).
Acknowledgements
This work has been supported by the EU integrated project QAP and STREP COMPAS, EPSRC grants EP/C546237/1 and QIP-IRC, the Royal Society, Microsoft Research and the EURYI Award Scheme. H.C.-R. has been supported by the European Commission under the Marie Curie Programme and by the Heinz-Durr Programme of the Studienstiftung des dt. Volkes.
Author information
Authors and Affiliations
Contributions
J.S.L., H.C-R. and I.A.W. contributed to the concept of the experiment and its design, as well as to laboratory measurements and data analysis. A.F., K.L.P., M.B.P. and J.E. contributed modelling and data analysis. Ch. S. and T.C.R. contributed to the conception of the project and to its planning.
Corresponding authors
Rights and permissions
About this article
Cite this article
Lundeen, J., Feito, A., Coldenstrodt-Ronge, H. et al. Tomography of quantum detectors. Nature Phys 5, 27–30 (2009). https://doi.org/10.1038/nphys1133
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/nphys1133
This article is cited by
-
Parallel tomography of quantum non-demolition measurements in multi-qubit devices
npj Quantum Information (2023)
-
Quantum simulation of thermodynamics in an integrated quantum photonic processor
Nature Communications (2023)
-
Nonlinear feedforward enabling quantum computation
Nature Communications (2023)
-
Near-term quantum computing techniques: Variational quantum algorithms, error mitigation, circuit compilation, benchmarking and classical simulation
Science China Physics, Mechanics & Astronomy (2023)
-
Implementation of single-qubit measurement-based t-designs using IBM processors
Scientific Reports (2022)
