Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Quantum interference and Klein tunnelling in graphene heterojunctions

Nature Physics volume 5, pages 222–226 (2009)Cite this article

Abstract

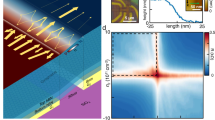
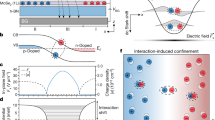
The observation of quantum conductance oscillations in mesoscopic systems has traditionally required the confinement of the carriers to a phase space of reduced dimensionality1,2,3,4. Although electron optics such as lensing5 and focusing6 have been demonstrated experimentally, building a collimated electron interferometer in two unconfined dimensions has remained a challenge owing to the difficulty of creating electrostatic barriers that are sharp on the order of the electron wavelength7. Here, we report the observation of conductance oscillations in extremely narrow graphene heterostructures where a resonant cavity is formed between two electrostatically created bipolar junctions. Analysis of the oscillations confirms that p–n junctions have a collimating effect on ballistically transmitted carriers8. The phase shift observed in the conductance fringes at low magnetic fields is a signature of the perfect transmission of carriers normally incident on the junctions9 and thus constitutes a direct experimental observation of ‘Klein tunnelling’10,11,12.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Graphene heterojunction device schematic diagrams and conductance measurements.
Figure 2: Density and magnetic-field dependence of the oscillatory conductance; origin of the Klein tunnelling phase shift.
Figure 3: Comparison of experimental data to the theoretical model, and temperature dependence.

Similar content being viewed by others

References

  1. van Wees, B. J. et al. Observation of zero-dimensional states in a one-dimensional electron interferometer. Phys. Rev. Lett. 62, 2523–2526 (1989).

    Article  ADS  Google Scholar 

  2. Ji, Y. et al. An electronic Mach-Zehnder interferometer. Nature 422, 415–418 (2003).

    Article  ADS  Google Scholar 

  3. Liang, W. et al. Fabry–Perot interference in a nanotube electron waveguide. Nature 411, 665–669 (2001).

    Article  ADS  Google Scholar 

  4. Miao, F. et al. Phase-coherent transport in graphene quantum billiards. Science 317, 1530–1533 (2007).

    Article  ADS  Google Scholar 

  5. Spector, J., Stormer, H. L., Baldwin, K. W., Pfeiffer, L. N. & West, K. W. Electron focusing in two-dimensional systems by means of an electrostatic lens. Appl. Phys. Lett. 56, 1290–1292 (1990).

    Article  ADS  Google Scholar 

  6. van Houten, H. & Beenakker, C. W. J. in Analogies in Optics and Micro Electronics (eds van Haeringen, W. & Lenstra, D.) (Kluwer, 1990).

    Google Scholar 

  7. Washburn, S., Fowler, A. B., Schmid, H. & Kern, D. Possible observation of transmission resonances in GaAs–AlxGa1−x As transistors. Phys. Rev. B 38, 1554–1557 (1988).

    Article  ADS  Google Scholar 

  8. Cheianov, V. V. & Fal’ko, V. I. Selective transmission of Dirac electrons and ballistic magnetoresistance of n–p junctions in graphene. Phys. Rev. B 74, 041403(R) (2006).

    Article  ADS  Google Scholar 

  9. Shytov, A. V., Rudner, M. S. & Levitov, L. S. Klein backscattering and Fabry–Perot interference in graphene heterojunctions. Phys. Rev. Lett. 101, 156804 (2008).

    Article  ADS  Google Scholar 

  10. Katsnelson, M. I., Novoselov, K. S. & Geim, A. K. Chiral tunnelling and the Klein paradox in graphene. Nature Phys. 2, 620–625 (2006).

    Article  ADS  Google Scholar 

  11. Klein, O. Die Reflexion von Elektronen an einem Potentialsprung nach der relativistischen Dynamik von Dirac. Z. Phys. 53, 157–165 (1929).

    Article  ADS  Google Scholar 

  12. Sauter, F. Über das Verhalten eines Elektrons im homogenen elektrischen Feld nach der relativistischen Theorie Diracs. 69 742–764 (1931).

  13. Ando, T. & Nakanishi, T. Impurity scattering in carbon nanotubes: Absence of backscattering. J. Phys. Soc. Jpn. 67, 1704–1713 (1998).

    Article  ADS  Google Scholar 

  14. Cheianov, V. V., Fal’ko, V. I. & Altshuler, B. L. The focusing of electron flow and a Veselago lens in graphene p–n junctions. Science 315, 1252–1255 (2007).

    Article  ADS  Google Scholar 

  15. Park, C.-H. et al. Anisotropic behaviours of massless Dirac fermions in graphene under periodic potentials. Nature Phys. 4, 213–217 (2008).

    Article  ADS  Google Scholar 

  16. Park, C.-H. et al. Electron beam supercollimation in graphene superlattices. Nano Lett. 8, 2920–2924 (2008).

    Article  ADS  Google Scholar 

  17. Garcia-Pomar, J. L., Cortijo, A. & Nieto-Vesperinas, M. Fully valley-polarized electron beams in graphene. Phys. Rev. Lett. 100, 236801 (2008).

    Article  ADS  Google Scholar 

  18. Lemme, M. C., Echtermeyer, T. J., Baus, M. & Kurz, H. A graphene field effect device. IEEE Electron Device Lett. 28, 282–284 (2007).

    Article  ADS  Google Scholar 

  19. Huard, B. et al. Transport measurements across a tunable potential barrier in graphene. Phys. Rev. Lett. 98, 236803 (2007).

    Article  ADS  Google Scholar 

  20. Williams, J. R., DiCarlo, L. & Marcus, C. M. Quantum Hall effect in a gate-controlled p–n junction of graphene. Science 317, 638–641 (2007).

    Article  ADS  Google Scholar 

  21. Özyilmaz, B. et al. Electronic transport and quantum Hall effect in bipolar graphene p–n–p junctions. Phys. Rev. Lett. 99, 166804 (2007).

    Article  ADS  Google Scholar 

  22. Gorbachev, R. V., Mayorov, A. S., Savchenko, A. K., Horsell, D. W. & Guinea, F. Conductance of p–n–p graphene structures with air-bridge top gates. Nano Lett. 8, 1995–1999 (2008).

    Article  ADS  Google Scholar 

  23. Liu, G., Velasco, J., Bao, W. & Lau, C. N. Fabrication of graphene p–n–p junctions with contactless top gates. Appl. Phys. Lett. 92, 203103 (2008).

    Article  ADS  Google Scholar 

  24. Stander, N., Huard, B. & Goldhaber-Gordon, D. Evidence of Klein tunneling in graphene p–n junctions. Preprint at <http://arxiv.org/abs/0806.2319> (2008).

  25. Meric, I. et al. Current saturation in zero-bandgap, top-gated graphene field-effect transistors. Nature Nanotech. 3, 654–659 (2008).

    Article  ADS  Google Scholar 

  26. Zhang, L. M. & Fogler, M. M. Nonlinear screening and ballistic transport in a graphene p–n junction. Phys. Rev. Lett. 100, 116804 (2008).

    Article  ADS  Google Scholar 

  27. Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005).

    Article  ADS  Google Scholar 

  28. Zhang, Y., Tan, Y. W., Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 438, 201–204 (2005).

    Article  ADS  Google Scholar 

  29. Ryu, S. et al. Reversible basal plane hydrogenation of graphene. Nano Lett. 8, 4597–4602 (2008).

    Article  ADS  Google Scholar 

  30. Bolotin, K. I. et al. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 146, 351–355 (2008).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The authors would like to thank I. L. Aleiner, K. I. Bolotin, M. Y. Han, E. A. Henriksen, L. S. Levitov and H. L. Stormer for discussions, and I. Meric and M. Y. Han for help with sample preparation. This work is supported by the ONR (No. N000150610138), FENA, NRI, NSEC (No. CHE-0117752) and NYSTAR. Sample preparation was supported by the DOE (DE-FG02-05ER46215).

Author information

Authors and Affiliations

  1. Department of Physics, Columbia University, New York 10027, USA

    Andrea F. Young & Philip Kim

Authors
  1. Andrea F. Young
    View author publications

    Search author on:PubMed Google Scholar

  2. Philip Kim
    View author publications

    Search author on:PubMed Google Scholar

Corresponding author

Correspondence to Philip Kim.

Supplementary information

Supplementary Information

Supplementary Informations (PDF 1027 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Young, A., Kim, P. Quantum interference and Klein tunnelling in graphene heterojunctions. Nature Phys 5, 222–226 (2009). https://doi.org/10.1038/nphys1198

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys1198

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing