Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

The quantum-optical Josephson interferometer

Nature Physics volume 5, pages 281–284 (2009)Cite this article

Abstract

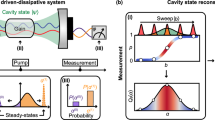
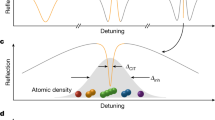
The photon-blockade effect, where nonlinearities at the single-photon level alter the quantum statistics of light emitted from a cavity1, has been observed in cavity quantum electrodynamics experiments with atomic2,3 and solid-state systems4,5,6,7,8. Motivated by the success of single-cavity quantum electrodynamics experiments, the focus has recently shifted to the exploration of the rich physics promised by strongly correlated quantum-optical systems in multicavity and extended photonic media9,10,11,12,13,14. Even though most cavity quantum electrodynamics structures are inherently dissipative, most of the early work on strongly correlated photonic systems has assumed cavity structures where losses are essentially negligible. Here we investigate a dissipative quantum-optical system that consists of two coherently driven linear optical cavities connected through a central cavity with a single-photon nonlinearity (an optical analogue of the Josephson interferometer). The interplay of tunnelling and interactions is analysed in the steady state of the system, when a dynamical equilibrium between driving and losses is established. Strong photonic correlations can be identified through the suppression of Josephson-like oscillations of the light emitted from the central cavity as the nonlinearity is increased. In the limit of a single nonlinear cavity coupled to two linear waveguides, we show that photon-correlation measurements would provide a unique probe of the crossover to the strongly correlated regime.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: The systems under consideration.
Figure 2: Numerical solutions for the three-cavity system.
Figure 3: Numerical solutions for the waveguide-coupled limit.

Similar content being viewed by others

References

  1. Werner, M. J. & Imamoglu, A. Photon–photon interactions in cavity electromagnetically induced transparency. Phys. Rev. A 61, R011801 (1999).

    Article  ADS  Google Scholar 

  2. Birnbaum, K. M. et al. Photon blockade in an optical cavity with one trapped atom. Nature 436, 87–90 (2005).

    Article  ADS  Google Scholar 

  3. Schuster, I. et al. Nonlinear spectroscopy of photons bound to one atom. Nature Phys. 4, 382–385 (2008).

    Article  ADS  Google Scholar 

  4. Schuster, D. I. et al. Resolving photon number states in a superconducting circuit. Nature 445, 515–518 (2007).

    Article  ADS  Google Scholar 

  5. Hennessy, K. et al. Quantum nature of a strongly coupled single quantum dot–cavity system. Nature 445, 896–899 (2007).

    Article  ADS  Google Scholar 

  6. Srinivasan, K. & Painter, O. Linear and nonlinear optical spectroscopy of a strongly coupled microdisc–quantum dot system. Nature 450, 862–865 (2007).

    Article  ADS  Google Scholar 

  7. Faraon, A. et al. Coherent generation of nonclassical light on a chip via photon-induced tunneling and blockade. Nature Phys. 4, 859–863 (2008).

    Article  ADS  Google Scholar 

  8. Bishop, L. S. et al. Nonlinear response of the vacuum Rabi resonance. Nature Phys. 5, 105–109 (2009).

    Article  ADS  Google Scholar 

  9. Hartmann, M. J., Brandão, F. G. S. L. & Plenio, M. B. Strongly interacting polaritons in coupled arrays of cavities. Nature Phys. 2, 849–855 (2006).

    Article  ADS  Google Scholar 

  10. Greentree, A. D., Tahan, C., Cole, J. H. & Hollenberg, L. C. L. Quantum phase transitions of light. Nature Phys. 2, 856–861 (2006).

    Article  ADS  Google Scholar 

  11. Angelakis, D. G., Santos, M. F. & Bose, S. Photon-blockade-induced Mott transitions and XY spin models in coupled cavity arrays. Phys. Rev. A 76, R031805 (2007).

    Article  ADS  Google Scholar 

  12. Chang, D. E. et al. Crystallization of strongly interacting photons in a nonlinear optical fibre. Nature Phys. 4, 884–889 (2008).

    Article  ADS  Google Scholar 

  13. Shen, J. T. & Fan, S. Strongly correlated two-photon transport in a one-dimensional waveguide coupled to a two-level system. Phys. Rev. Lett. 98, 153003 (2007).

    Article  ADS  Google Scholar 

  14. Zhou, L., Gong, Z. L., Liu, Y., Sun, C. P. & Nori, F. Controllable scattering of a single photon inside a one-dimensional resonator waveguide. Phys. Rev. Lett. 101, 100501 (2008).

    Article  ADS  Google Scholar 

  15. Jaynes, E. T. & Cummings, F. W. Comparison of quantum and semiclassical radiation theory with application to the beam maser. Proc. IEEE 51, 89–109 (1963).

    Article  Google Scholar 

  16. Verger, A., Ciuti, C. & Carusotto, I. Polariton quantum blockade in a photonic dot. Phys. Rev. B 73, 193306 (2006).

    Article  ADS  Google Scholar 

  17. Averin, D. V. & Likharev, K. K. in Mesoscopic Phenomena in Solids (eds Altshuler, B. L., Lee, P. A. & Webb, R. A.) 213 (North Holland, 1991).

    Google Scholar 

  18. Matveev, K. A., Gisselfält, M., Glazman, L. I., Jonson, M. & Shekhter, R. I. Parity-induced suppression of the Coulomb blockade of Josephson tunneling. Phys. Rev. Lett. 70, 2940–2943 (1993).

    Article  ADS  Google Scholar 

  19. Geerligs, L. J., de Groot, L. E. M., Verbruggen, A. & Mooji, J. E. Charging effects and quantum coherence in regular Josephson junction arrays. Phys. Rev. Lett. 63, 326–329 (1989).

    Article  ADS  Google Scholar 

  20. Elion, W. J., Matters, M., Geigenmüller, U. & Mooji, J. E. Direct demonstration of Heisenberg uncertainty principle in a superconductor. Nature 371, 594–595 (1994).

    Article  ADS  Google Scholar 

  21. Carmichael, H. An Open Systems Approach to Quantum Optics (Springer, 1993).

    MATH  Google Scholar 

  22. Atlasov, K. A., Karlsson, K. F., Rudra, A., Dwir, B. & Kapon, E. Wavelength and loss splitting in directly coupled photonic-crystal defect microcavities. Opt. Express 16, 16255–16264 (2008).

    Article  ADS  Google Scholar 

  23. Combrié, S., De Rossi, A., Tran, Q. V. & Benisty, H. GaAs photonic crystal cavity with ultrahigh Q: Microwatt nonlinearity at 1.55 μm. Opt. Lett. 33, 1908–1910 (2008).

    Article  ADS  Google Scholar 

  24. Jakob, M. & Stenholm, S. Variational functions in driven open quantum systems. Phys. Rev. A 67, 032111 (2003).

    Article  ADS  Google Scholar 

  25. Diehl, S. et al. Quantum states and phases in driven open quantum systems with cold atoms. Nature Phys. 4, 878–883 (2008).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The authors would like to acknowledge discussions with I. Carusotto, C. Ciuti and S. De Liberato. This work was partly supported by NCCR Quantum Photonics. D.G. acknowledges financial support from Fondazione Cariplo. A.I. acknowledges financial support from an ERC Advanced Investigator grant. R.F. acknowledges financial support from EUROSQIP.

Author information

Authors and Affiliations

  1. Institute of Quantum Electronics, ETH Zurich, 8093 Zurich, Switzerland

    Dario Gerace, Hakan E. Türeci & Atac Imamoglu

  2. CNISM and Dipartimento di Fisica ‘A. Volta’, Università di Pavia, 27100 Pavia, Italy

    Dario Gerace

  3. NEST CNR-INFM and Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy

    Vittorio Giovannetti & Rosario Fazio

  4. International School for Advanced Studies (SISSA), via Beirut 2–4, 34014 Trieste, Italy

    Rosario Fazio

Authors
  1. Dario Gerace
    View author publications

    Search author on:PubMed Google Scholar

  2. Hakan E. Türeci
    View author publications

    Search author on:PubMed Google Scholar

  3. Atac Imamoglu
    View author publications

    Search author on:PubMed Google Scholar

  4. Vittorio Giovannetti
    View author publications

    Search author on:PubMed Google Scholar

  5. Rosario Fazio
    View author publications

    Search author on:PubMed Google Scholar

Corresponding author

Correspondence to Dario Gerace.

Supplementary information

Supplementary Information

Supplementary Informations (PDF 334 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gerace, D., Türeci, H., Imamoglu, A. et al. The quantum-optical Josephson interferometer. Nature Phys 5, 281–284 (2009). https://doi.org/10.1038/nphys1223

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys1223

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing