Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Propulsion generated by diffusion-driven flow

Nature Physics volume 6, pages 516–519 (2010)Cite this article

Abstract

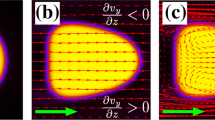
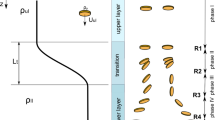
Buoyancy-driven flow, which is flow driven by spatial variations in fluid density1, lies at the heart of a variety of physical processes, including mineral transport in rocks2, the melting of icebergs3 and the migration of tectonic plates4. Here we show that buoyancy-driven flows can also generate propulsion. Specifically, we find that when a neutrally buoyant wedge-shaped object floats in a density-stratified fluid, the diffusion-driven flow at its sloping boundaries generated by molecular diffusion produces a macroscopic sideways thrust. Computer simulations reveal that thrust results from diffusion-driven flow creating a region of low pressure at the front, relative to the rear of an object. This discovery has implications for transport processes in regions of varying fluid density, such as marine snow aggregation at ocean pycnoclines5, and wherever there is a temperature difference between immersed objects and the surrounding fluid, such as particles in volcanic clouds6.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Spontaneous propulsion of a triangular wedge in a density-stratified fluid.
Figure 2: PIV visualizations of the flow field around a moving wedge.
Figure 3: Experimental results for u as a function of the governing parameters.
Figure 4: Numerical simulation of diffusion-driven flow induced by a fixed wedge.

Similar content being viewed by others

References

  1. Turner, J. S. Buoyancy Effects in Fluids (Cambridge Univ. Press, 1973).

    Book  Google Scholar 

  2. Phillips, O. M. On flows induced by diffusion in a stably stratified fluid. Deep-Sea Res. 17, 435–443 (1970).

    Google Scholar 

  3. Huppert, H. E. & Turner, J. S. On melting icebergs. Nature 271, 46–48 (1978).

    Article  ADS  Google Scholar 

  4. Gurnis, M. Large-scale mantle convection and the aggregation and dispersal of supercontinents. Nature 332, 695–699 (1988).

    Article  ADS  Google Scholar 

  5. MacIntyre, S., Alldredge, A. L. & Gotschalk, C. C. Accumulation of marine snow at density discontinuities in the water column. Limnol. Oceanogr. 40, 449–468 (1995).

    Article  ADS  Google Scholar 

  6. Hoyal, D. C. J. D., Bursik, M. I. & Atkinson, J. F. Settling-driven convection: A mechanism of sedimentation from stratified fluids. J. Geophys. Res. 104, 7953–7966 (1999).

    Article  ADS  Google Scholar 

  7. Wunsch, C. On oceanic boundary mixing. Deep-Sea Res. 17, 293–301 (1970).

    Google Scholar 

  8. Buckingham, E. The principle of similitude. Nature 96, 396–397 (1915).

    Article  ADS  Google Scholar 

  9. Peacock, T., Stocker, R. & Aristoff, J. An experimental investigation of the angular dependence of diffusion-driven flow. Phys. Fluids 16, 3503–3505 (2004).

    Article  ADS  Google Scholar 

  10. Woods, A. W. Boundary-driven mixing. J. Fluid Mech. 226, 625–654 (1991).

    Article  ADS  MathSciNet  Google Scholar 

  11. Page, M. A. & Johnson, E. R. Steady nonlinear diffusion-driven flow. J. Fluid Mech. 629, 299–309 (2009).

    Article  ADS  MathSciNet  Google Scholar 

  12. Cordova-Figueroa, U. M. & Brady, J. F. Osmotic propulsion: The osmotic motor. Phys. Rev. Lett. 100, 158303 (2008).

    Article  ADS  Google Scholar 

  13. Prandtl, L. The Essentials of Fluid Dynamics (Blackie, 1952).

    MATH  Google Scholar 

  14. Oerlemans, J. & Grisogono, B. Glacier winds and parameterization of the related heat fluxes. Tellus 54A, 440–452 (2002).

    Article  ADS  Google Scholar 

  15. Ferrari, R. & Wunsch, C. Ocean circulation kinetic energy: Reservoirs, sources and sinks. Annu. Rev. Fluid Mech. 41, 253–282 (2009).

    Article  ADS  Google Scholar 

  16. Barad, M. F., Colella, P. & Schladow, S. G. An adaptive cut-cell method for environmental fluid mechanics. Int. J. Numer. Meth. Fluids 60, 473–514 (2009).

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

We thank R. Stocker, E. Lauga and C. C. Mei for discussions; W. Etheridge, P. Steinmetz and C. Lenahan for experimental assistance; A. Gallant for fabrication of experimental apparatus; O. Fringer for access to computational resources; and G. Buck, J. W. M. Bush, E. Johnson, W. R. Young, C. Wunsch and J. H. Peacock for reading the manuscript. This work was supported by the NSF CBET programme. M.F.B. acknowledges the support of the National Science Foundation MSPRF programme. This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the US Department of Energy under Contract No. DE-AC02-05CH11231.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA

    Michael R. Allshouse & Thomas Peacock

  2. Environmental Fluid Mechanics Laboratory, Stanford University, Yang & Yamasaki Environment & Energy Building, 473 Via Ortega, Office M15, Stanford, California 94305, USA

    Michael F. Barad

Authors
  1. Michael R. Allshouse
    View author publications

    Search author on:PubMed Google Scholar

  2. Michael F. Barad
    View author publications

    Search author on:PubMed Google Scholar

  3. Thomas Peacock
    View author publications

    Search author on:PubMed Google Scholar

Contributions

T.P. conceived the original idea, supervised the research and wrote the manuscript. M.R.A. carried out the experiments, ran some numerical simulations and analysed the numerical data. M.F.B. ran the stratified flow simulations.

Corresponding author

Correspondence to Thomas Peacock.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 349 kb)

Supplementary Movie

Supplementary Movie 1 (MOV 9929 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Allshouse, M., Barad, M. & Peacock, T. Propulsion generated by diffusion-driven flow. Nature Phys 6, 516–519 (2010). https://doi.org/10.1038/nphys1686

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys1686

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing