Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

The Peregrine soliton in nonlinear fibre optics

Nature Physics volume 6, pages 790–795 (2010)Cite this article

Abstract

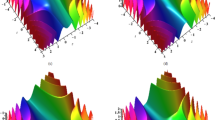
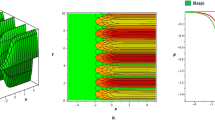
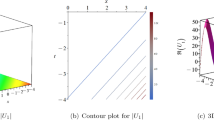
The Peregrine soliton is a localized nonlinear structure predicted to exist over 25 years ago, but not so far experimentally observed in any physical system1. It is of fundamental significance because it is localized in both time and space, and because it defines the limit of a wide class of solutions to the nonlinear Schrödinger equation (NLSE). Here, we use an analytic description of NLSE breather propagation2 to implement experiments in optical fibre generating femtosecond pulses with strong temporal and spatial localization, and near-ideal temporal Peregrine soliton characteristics. In showing that Peregrine soliton characteristics appear with initial conditions that do not correspond to the mathematical ideal, our results may impact widely on studies of hydrodynamic wave instabilities where the Peregrine soliton is considered a freak-wave prototype3,4,5,6,7.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Plotted Akhmediev breather solutions using equation (2) for modulation parameter a=0.25, a=0.45 and a=0.48, as well as the ideal Peregrine soliton of equation (3), the limiting case of the Akhmediev breather as a→1/2.
Figure 2: Evolution towards Peregrine soliton characteristics with increasing modulation parameter for temporal profile characteristics and localization behaviour.
Figure 3: Experimental set-up.
Figure 4: The variation in temporal and spectral characteristics with normalized propagation distance to confirm expected dynamical evolution.
Figure 5: Experimental results showing the measured temporal characteristics of the maximally compressed pulse at ξ=2.5, and comparison with the predicted Peregrine soliton.

Similar content being viewed by others

References

  1. Peregrine, D. H. Water waves, nonlinear Schrödinger equations and their solutions. J. Aust. Math. Soc. Ser. B 25, 16–43 (1983).

    Article  MATH  Google Scholar 

  2. Akhmediev, N. & Korneev, V. I. Modulation instability and periodic solutions of the nonlinear Schrödinger equation. Theor. Math. Phys. 69, 1089–1093 (1986).

    Article  MATH  Google Scholar 

  3. Henderson, K. L, Peregrine, D. H. & Dold, J. W. Unsteady water wave modulations: Fully nonlinear solutions and comparison with the nonlinear Schrödinger equation. Wave Motion 29, 341–361 (1999).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. Dysthe, K. B. & Trulsen, K. Note on breather type solutions of the NLS as models for freak-waves. Phys. Scripta 82, 48–52 (1999).

    Article  MATH  Google Scholar 

  5. Kharif, C., Pelinovsky, E. & Slunyaev, A. Rogue Waves in the Ocean (Springer-Verlag, 2009).

    MATH  Google Scholar 

  6. Akhmediev, N., Soto-Crespo, J. M. & Ankiewicz, A. Extreme waves that appear from nowhere: On the nature of rogue waves. Phys. Lett. A 373, 2137–2145 (2009).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. Shrira, V. I. & Geoigjaev, V. V. What makes the Peregrine soliton so special as a prototype of freak waves? J. Eng. Math. 67, 11–22 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  8. Taylor, J. R. (ed.) Optical Solitons Theory & Experiment (Cambridge Univ. Press, 1992).

  9. Dauxois, Th. & Peyrard, M. Physics of Solitons (Cambridge Univ. Press, 2006).

    MATH  Google Scholar 

  10. Denschlag, J. et al. Generating solitons by phase engineering of a Bose–Einstein condensate. Science 287, 97–101 (2000).

    Article  ADS  Google Scholar 

  11. Fermi, E., Pasta, J. & Ulam, S. in Collected Papers of Enrico Fermi (ed. Segre, E.) 978–988 (Univ. Chicago Press, 1965).

    MATH  Google Scholar 

  12. Akhmediev, N. & Ankiewicz, A. Solitons, Nonlinear Pulses and Beams (Chapman and Hall, 1997).

    MATH  Google Scholar 

  13. Sato, M. & Sievers, A. J. Direct observation of the discrete character of intrinsic localized modes in an antiferromagnet. Nature 432, 486–488 (2004).

    Article  ADS  MATH  Google Scholar 

  14. Bespalov, V. I. & Talanov, V. J. Filamentary structure of light beams in nonlinear liquids. JETP Lett. 3, 307–310 (1966).

    ADS  MATH  Google Scholar 

  15. Benjamin, T. B. & Feir, J. E. The disintegration of wavetrains on deep water. Part 1: Theory. J. Fluid Mech. 27, 417–430 (1967).

    Article  ADS  MATH  Google Scholar 

  16. Hasegawa, A. Generation of a train of soliton pulses by induced modulational instability in optical fibres. Opt. Lett. 9, 288–290 (1984).

    Article  ADS  MATH  Google Scholar 

  17. Tai, K., Tomita, A., Jewell, J. L. & Hasegawa, A. Generation of subpicosecond solitonlike optical pulses at 0.3 THz repetition rate by induced modulational instability. Appl. Phys. Lett. 49, 236–238 (1986).

    Article  ADS  Google Scholar 

  18. Hart, D. L., Judy, A. F., Roy, R. & Beletic, J. W. Dynamical evolution of multiple four-wave-mixing processes in an optical fiber. Phys. Rev. E 57, 4757–4774 (1998).

    Article  ADS  MATH  Google Scholar 

  19. Greer, E. J., Patrick, D. M., Wigley, P. G. J. & Taylor, J. R. Generation of 2 THz repetition rate pulse trains through induced modulational instability. Electron. Lett. 25, 1246–1248 (1989).

    Article  ADS  MATH  Google Scholar 

  20. Mamyshev, P. V., Chernikov, S. V., Dianov, E. M. & Prokhorov, A. M. Generation of a high-repetition-rate train of practically noninteracting solitons by using the induced modulational instability and Raman self-scattering effects. Opt. Lett. 15, 1365–1367 (1990).

    Article  ADS  Google Scholar 

  21. Trillo, S. & Wabnitz, S. Dynamics of the nonlinear modulational instability in optical fibres. Opt. Lett. 16, 986–988 (1991).

    Article  ADS  MATH  Google Scholar 

  22. Fatome, J., Pitois, S. & Millot, G. 20-GHz-to-1-THz repetition rate pulse sources based on multiple four-wave mixing in optical fibers. IEEE J. Quantum Electron. 42, 1038–1046 (2006).

    Article  ADS  MATH  Google Scholar 

  23. Van Simaeys, G., Emplit, Ph. & Haelterman, M. Experimental demonstration of the Fermi–Pasta–Ulam recurrence in a modulationally unstable optical wave. Phys. Rev. Lett. 87, 033902 (2001).

    Article  ADS  MATH  Google Scholar 

  24. Dudley, J. M., Genty, G., Dias, F., Kibler, B. & Akhmediev, N. Modulation instability, Akhmediev Breathers and continuous wave supercontinuum generation. Opt. Exp. 17, 21497–21508 (2009).

    Article  MATH  Google Scholar 

  25. Dudley, J. M., Finot, C., Richardson, D. J. & Millot, G. Self similarity in ultrafast nonlinear optics. Nature Phys. 3, 597–603 (2007).

    Article  ADS  MATH  Google Scholar 

  26. Solli, D. R., Ropers, C., Koonath, P. & Jalali, B. Optical rogue waves. Nature 450, 1054–1057 (2007).

    Article  ADS  Google Scholar 

  27. Doktorov, E. V., Rothos, V. M. & Kivshar, Y. S. Full-time dynamics of modulational instability in spinor Bose–Einstein condensates. Phys. Rev. A 76, 013626 (2007).

    Article  ADS  MATH  Google Scholar 

  28. Agrawal, G. P. Nonlinear Fibre Optics 4th edn (Academic, 2007).

    MATH  Google Scholar 

  29. Dudley, J. M. et al. Complete intensity and phase characterisation of optical pulse trains at THz repetition rates. Electron. Lett. 35, 2042–2044 (1999).

    Article  ADS  MATH  Google Scholar 

  30. Dudley, J. M., Genty, G. & Coen, S. Supercontinuum generation in photonic crystal fibre. Rev. Mod. Phys. 78, 1135–1184 (2006).

    Article  ADS  MATH  Google Scholar 

Download references

Acknowledgements

We acknowledge support from the French Agence Nationale de la Recherche projects MANUREVA ANR-08-SYSC-019 and IMFINI ANR-09-BLAN-0065, the Academy of Finland Research grants 132279 and 130099, the 2008 Framework Program for Research, Technological development and Innovation of the Cyprus Research Promotion Foundation under the Project ASTI/0308(BE)/05 and the Australian Research Council Discovery Project scheme DP0985394.

Author information

Authors and Affiliations

  1. Laboratoire Interdisciplinaire Carnot de Bourgogne, UMR 5209 CNRS — Université de Bourgogne, Dijon, France

    B. Kibler, J. Fatome, C. Finot & G. Millot

  2. Centre de Mathématiques et de Leurs Applications (CMLA), ENS Cachan, 94230 Cachan, France

    F. Dias

  3. UCD School of Mathematical Sciences, University College Dublin, Belfield, Dublin 4, Ireland

    F. Dias

  4. Tampere University of Technology, Optics Laboratory, FI-33101 Tampere, Finland

    G. Genty

  5. Optical Sciences Group, Research School of Physics and Engineering, Institute of Advanced Studies, The Australian National University, Canberra ACT 0200, Australia

    N. Akhmediev

  6. Institut FEMTO-ST, UMR 6174 CNRS— Université de Franche-Comté, 25030 Besançon, France

    J. M. Dudley

Authors
  1. B. Kibler
    View author publications

    Search author on:PubMed Google Scholar

  2. J. Fatome
    View author publications

    Search author on:PubMed Google Scholar

  3. C. Finot
    View author publications

    Search author on:PubMed Google Scholar

  4. G. Millot
    View author publications

    Search author on:PubMed Google Scholar

  5. F. Dias
    View author publications

    Search author on:PubMed Google Scholar

  6. G. Genty
    View author publications

    Search author on:PubMed Google Scholar

  7. N. Akhmediev
    View author publications

    Search author on:PubMed Google Scholar

  8. J. M. Dudley
    View author publications

    Search author on:PubMed Google Scholar

Contributions

B.K., J.F., C.F. and J.M.D. carried out experiments. The development of analytical tools and simulations was carried out by B.K., G.M., G.G., F.D., N.A. and J.M.D. All authors participated in the analysis and interpretation of the results and the writing of the paper.

Corresponding author

Correspondence to J. M. Dudley.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kibler, B., Fatome, J., Finot, C. et al. The Peregrine soliton in nonlinear fibre optics. Nature Phys 6, 790–795 (2010). https://doi.org/10.1038/nphys1740

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys1740

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing