Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Upscale energy transfer in thick turbulent fluid layers

Nature Physics volume 7, pages 321–324 (2011)Cite this article

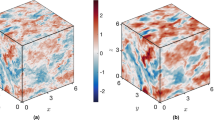
Abstract

Flows in natural fluid layers are often forced simultaneously at scales smaller and much larger than the depth. For example, the Earth’s atmospheric flows are powered by gradients of solar heating: vertical gradients cause three-dimensional (3D) convection whereas horizontal gradients drive planetary scale flows. Nonlinear interactions spread energy over scales1,2. The question is whether intermediate scales obtain their energy from a large-scale 2D flow or from a small-scale 3D turbulence. The paradox is that 2D flows do not transfer energy downscale whereas 3D turbulence does not support an upscale transfer. Here we demonstrate experimentally how a large-scale vortex and small-scale turbulence conspire to provide for an upscale energy cascade in thick layers. We show that a strong planar vortex suppresses vertical motions, thus facilitating an upscale energy cascade. In a bounded system, spectral condensation into a box-size vortex provides for a self-organized planar flow that secures an upscale energy transfer.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Structure of turbulence in the double layer configuration.
Figure 2: Effects of externally imposed large-scale flow on turbulence in a single fluid layer (thickness h=10 mm, forcing scale lf=8 mm).

Similar content being viewed by others

References

  1. Lilly, D. K. & Petersen, E. L. Aircraft measurements of atmospheric kinetic energy spectra. Tellus 35A, 379–382 (1983).

    Article  ADS  Google Scholar 

  2. Nastrom, G. D., Gage, K. S. & Jasperson, W. H. The kinetic energy spectrum of large- and mesoscale atmospheric processes. Nature 310, 36–38 (1984).

    Article  ADS  Google Scholar 

  3. Kraichnan, R. H. Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423 (1967).

    Article  ADS  MathSciNet  Google Scholar 

  4. Sommeria, J. Experimental study of the two-dimensional inverse energy cascade in a square box. J. Fluid Mech. 170, 139–168 (1986).

    Article  ADS  Google Scholar 

  5. Paret, J. & Tabeling, P. Intermittency in the two-dimensional inverse cascade of energy: Experimental observations. Phys. Fluids 10, 3126–3136 (1998).

    Article  ADS  Google Scholar 

  6. Shats, M., Xia, H. & Punzmann, H. Spectral condensation of turbulence in plasmas and fluids and its role in low-to-high phase transitions in toroidal plasma. Phys. Rev. E 71, 046409 (2005).

    Article  ADS  Google Scholar 

  7. Vorobieff, P., Rivera, M. & Ecke, R. E. Soap film flows: Statistics of two-dimensional turbulence. Phys. Fluids 11, 2167–2177 (1999).

    Article  ADS  MathSciNet  Google Scholar 

  8. Belmonte, A. et al. Velocity fluctuations in a turbulent soap film: The third moment in two dimensions. Phys. Fluids 11, 1196–1200 (1999).

    Article  ADS  Google Scholar 

  9. Smith, L. M., Chasnov, J. R. & Fabian, W. Crossover from two- to three-dimensional turbulence. Phys. Rev. Lett. 77, 2467–2470 (1996).

    Article  ADS  Google Scholar 

  10. Celani, A., Musacchio, S. & Vincenzi, D. Turbulence in more than two and less than three dimensions. Phys. Rev. Lett. 104, 184506 (2010).

    Article  ADS  Google Scholar 

  11. Shats, M. G., Xia, H., Punzmann, H. & Falkovich, G. Suppression of turbulence by self-generated and imposed mean flows. Phys. Rev. Lett. 99, 164502 (2007).

    Article  ADS  Google Scholar 

  12. Xia, H., Punzmann, H., Falkovich, G. & Shats, M. Turbulence-condensate interaction in two dimensions. Phys. Rev. Lett. 101, 194504 (2008).

    Article  ADS  Google Scholar 

  13. Xia, H., Shats, M. & Falkovich, G. Spectrally condensed turbulence in thin layers. Phys. Fluids 21, 125101 (2009).

    Article  ADS  Google Scholar 

  14. Willert, C. E. & Gharib, M. Three-dimensional particle imaging with a single camera. Exp. Fluids 12, 353–358 (1992).

    Article  Google Scholar 

  15. Chertkov, M., Connaughton, C., Kolokolov, I. & Lebedev, V. Dynamics of energy condensation in two-dimensional turbulence. Phys. Rev. Lett. 99, 084501 (2007).

    Article  ADS  Google Scholar 

  16. Hopfinger, E. J., Browand, F. K. & Gagne, Y. Turbulence and waves in a rotating tank. J. Fluid Mech. 125, 505–534 (1982).

    Article  ADS  Google Scholar 

  17. Spiegel, E. A. & Zahn, J-P. The solar tachocline. Astron. Astrophys. 265, 106–114 (1992).

    ADS  Google Scholar 

  18. Kim, E-J. Self-consistent theory of turbulent transport in the solar tachocline. Astron. Astrophys. 441, 763–772 (2005).

    Article  ADS  Google Scholar 

  19. Frisch, U. Turbulence: The Legacy of A.N. Kolmogorov (Cambridge Univ. Press, 1995).

    Book  Google Scholar 

  20. Gage, K. S. & Nastrom, G. D. Theoretical interpretation of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft during GASP. J. Atmos. Sci. 43, 729–740 (1986).

    Article  ADS  Google Scholar 

  21. Lilly, D. K. Two-dimensional turbulence generated by energy sources at two scales. J. Atmos. Sci 46, 2026–2030 (1989).

    Article  ADS  Google Scholar 

  22. Falkovich, G. Inverse cascade and wave condensate in mesoscale atmospheric turbulence. Phys. Rev. Lett. 69, 3173–3176 (1992).

    Article  ADS  Google Scholar 

  23. Smith, L. & Yakhot, V. Finite-size effects in forced two-dimensional turbulence. J. Fluid Mech. 274, 115–138 (1994).

    Article  ADS  MathSciNet  Google Scholar 

  24. Cho, J. Y. N. & Lindborg, E. Horizontal velocity structure functions in the upper troposphere and lower stratosphere. J. Geophys. Res. 106, 10223–10232 (2001).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the Australian Research Council’s Discovery Projects funding scheme (DP0881544) and by the Minerva Foundation and the Israeli Science Foundation.

Author information

Authors and Affiliations

  1. Research School of Physics and Engineering, The Australian National University, Canberra ACT 0200, Australia

    H. Xia, D. Byrne & M. Shats

  2. Physics of Complex Systems, Weizmann Institute of Science, Rehovot 76100, Israel

    G. Falkovich

Authors
  1. H. Xia
    View author publications

    Search author on:PubMed Google Scholar

  2. D. Byrne
    View author publications

    Search author on:PubMed Google Scholar

  3. G. Falkovich
    View author publications

    Search author on:PubMed Google Scholar

  4. M. Shats
    View author publications

    Search author on:PubMed Google Scholar

Contributions

H.X., D.B. and M.S. designed and performed experiments; H.X. and D.B. analysed the data. M.S. and G.F. wrote the paper. All authors discussed and edited the manuscript.

Corresponding author

Correspondence to M. Shats.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Xia, H., Byrne, D., Falkovich, G. et al. Upscale energy transfer in thick turbulent fluid layers. Nature Phys 7, 321–324 (2011). https://doi.org/10.1038/nphys1910

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys1910

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing