Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Experimental demonstration of a universally valid error–disturbance uncertainty relation in spin measurements

Nature Physics volume 8, pages 185–189 (2012)Cite this article

Subjects

A Corrigendum to this article was published on 01 August 2012

A Corrigendum to this article was published on 02 April 2012

This article has been updated

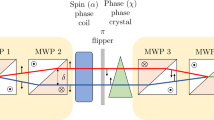
Abstract

The uncertainty principle generally prohibits simultaneous measurements of certain pairs of observables and forms the basis of indeterminacy in quantum mechanics1. Heisenberg’s original formulation, illustrated by the famous γ-ray microscope, sets a lower bound for the product of the measurement error and the disturbance2. Later, the uncertainty relation was reformulated in terms of standard deviations3,4,5, where the focus was exclusively on the indeterminacy of predictions, whereas the unavoidable recoil in measuring devices has been ignored6. A correct formulation of the error–disturbance uncertainty relation, taking recoil into account, is essential for a deeper understanding of the uncertainty principle, as Heisenberg’s original relation is valid only under specific circumstances7,8,9,10. A new error–disturbance relation, derived using the theory of general quantum measurements, has been claimed to be universally valid11,12,13,14. Here, we report a neutron-optical experiment that records the error of a spin-component measurement as well as the disturbance caused on another spin-component. The results confirm that both error and disturbance obey the new relation but violate the old one in a wide range of an experimental parameter.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Concept of the experiment.
Figure 2: Illustration of the experimental apparatus.
Figure 3: Experimental results.
Figure 4: Trade-off relation between error and disturbance.
Figure 5: Experimentally determined values of the universally valid uncertainty relation.

Similar content being viewed by others

Change history

  • 12 March 2012

    In the version of this Letter originally published, in Fig. 5a a factor of ℏ/2 appeared incorrectly against the label 'Heisenberg lower limit' and in the figure caption. This error has been corrected in the HTML and PDF versions of the Letter.

  • 01 August 2012

    In the version of this Letter originally published, in the Methods section under the heading 'Error and disturbance in spin measurements: theoretical determination' the equation defining η(B) was incorrect — the term σϕ should have been divided by 2. This error has been corrected in the HTML and PDF versions of the Letter.

References

  1. Wheeler, J. A. & Zurek, W. H. (eds) in Quantum Theory and Measurement (Princeton Univ. Press, 1983).

  2. Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 43, 172–198 (1927).

    Article  ADS  Google Scholar 

  3. Kennard, E. H. Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys. 44, 326–352 (1927).

    Article  ADS  Google Scholar 

  4. Robertson, H. P. The uncertainty principle. Phys. Rev. 34, 163–164 (1929).

    Article  ADS  Google Scholar 

  5. Schrödinger, E. Zum Heisenbergschen Unschärfeprinzip. Sitz. Preuss. Akad. Wiss. 14, 296–303 (1930).

    MATH  Google Scholar 

  6. Ballentine, L. E. The statistical interpretation of quantum mechanics. Rev. Mod. Phys. 42, 358–381 (1970).

    ADS  MATH  Google Scholar 

  7. Arthurs, E. & Kelly, J. L. Jr On the simultaneous measurement of a pair of conjugate observables. Bell Syst. Tech. J. 44, 725–729 (1965).

    Article  Google Scholar 

  8. Arthurs, E. & Goodman, M. S. Quantum correlations: A generalized Heisenberg uncertainty relation. Phys. Rev. Lett. 60, 2447–2449 (1988).

    Article  ADS  MathSciNet  Google Scholar 

  9. Ishikawa, S. Uncertainty relations in simultaneous measurements for arbitrary observables. Rep. Math. Phys. 29, 257–273 (1991).

    Article  ADS  MathSciNet  Google Scholar 

  10. Ozawa, M. in Quantum Aspects of Optical Communications. (eds Bendjaballah, C., Hirota, O. & Reynaud, S.) (Lecture Notes in Physics, Vol. 378, 3–17, Springer, 1991).

  11. Ozawa, M. Universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance in measurements. Phys. Rev. A 67, 042105 (2003).

    Article  ADS  Google Scholar 

  12. Ozawa, M. Physical content of the Heisenberg uncertainty relation: Limitation and reformulation. Phys. Lett. A 318, 21–29 (2003).

    Article  ADS  MathSciNet  Google Scholar 

  13. Ozawa, M. Uncertainty relations for noise and disturbance in generalized quantum measurements. Ann. Phys. 311, 350–416 (2004).

    Article  ADS  MathSciNet  Google Scholar 

  14. Ozawa, M. Universal uncertainty principle in measurement operator formalism. J. Opt. B 7, S672–S681 (2005).

    Article  ADS  MathSciNet  Google Scholar 

  15. Shull, C. G. Single slit diffraction of neutrons. Phys. Rev. 179, 752–754 (1969).

    Article  ADS  Google Scholar 

  16. Yuen, H. P. Two-photon coherent states of the radiation field. Phys. Rev. A 13, 2226–2243 (1976).

    Article  ADS  Google Scholar 

  17. Breitenbach, G., Schiller, S. & Mlynek, J. Measurement of the quantum states of squeezed light. Nature 387, 471–475 (1997).

    Article  ADS  Google Scholar 

  18. Appleby, D. M. The error principle. Int. J. Theor. Phys. 37, 2557–2572 (1998).

    Article  MathSciNet  Google Scholar 

  19. Werner, R. F. The uncertainty relation for joint measurement of position and momentum. Quant. Inf. Comput. 4, 546–562 (2004).

    ADS  MathSciNet  MATH  Google Scholar 

  20. Busch, P., Heinonen, T. & Lahti, P. Heisenberg’s uncertainty principle. Phys. Rep. 452, 155–176 (2007).

    Article  ADS  Google Scholar 

  21. Klepp, J. et al. Observation of nonadditive mixed-state phases with polarized neutrons. Phys. Rev. Lett. 101, 150404 (2008).

    Article  ADS  Google Scholar 

  22. Koshino, K. & Shimizu, A. Quantum Zeno effect by general measurements. Phys. Rep. 412, 191–275 (2005).

    Article  ADS  MathSciNet  Google Scholar 

  23. Mir, R. et al. A double-slit ‘which-way’ experiment on the Complementarity–uncertainty debate. New J. Phys. 9, 287 (2007).

    Article  ADS  Google Scholar 

  24. Lund, A. P. & Wiseman, H. M. Measuring measurement–disturbance relationships with weak values. New J. Phys. 12, 093011 (2010).

    Article  ADS  Google Scholar 

  25. Williams, G. Polarized Neutrons (Oxford Univ. Press, 1988).

    Google Scholar 

  26. Yuen, H. P. Contractive states and the standard quantum limit for monitoring free-mass positions. Phys. Rev. Lett. 51, 719–722 (1983).

    Article  ADS  Google Scholar 

  27. Ozawa, M. Measurement breaking the standard quantum limit for free-mass position. Phys. Rev. Lett. 60, 385–388 (1988).

    Article  ADS  Google Scholar 

  28. Maddox, J. Beating the quantum limits. Nature 331, 559 (1988).

    Article  ADS  Google Scholar 

  29. Nielsen, M. A. & Chuang, I. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).

    MATH  Google Scholar 

  30. Kraus, K. States, Effects, and Operations: Fundamental Notions of Quantum Theory (Lecture Notes in Physics, Vol. 190, Springer, 1983).

    Book  Google Scholar 

Download references

Acknowledgements

We acknowledge support by the Austrian Science Fund (FWF), the European Research Council (ERC), the Japan Science and Technology Agency (JST) and The Ministry of Education, Culture, Sports, Science and Technology (MEXT) in Japan. We thank H. Rauch, M. Arndt (Vienna) and A. Hosoya (Tokyo) for their helpful comments.

Author information

Authors and Affiliations

  1. Atominstitut, Vienna University of Technology, Stadionallee 2, 1020 Vienna, Austria

    Jacqueline Erhart, Stephan Sponar, Georg Sulyok, Gerald Badurek & Yuji Hasegawa

  2. Graduate School of Information Science, Nagoya University, Chikusa-ku, Nagoya 464-8601, Japan

    Masanao Ozawa

Authors
  1. Jacqueline Erhart
    View author publications

    Search author on:PubMed Google Scholar

  2. Stephan Sponar
    View author publications

    Search author on:PubMed Google Scholar

  3. Georg Sulyok
    View author publications

    Search author on:PubMed Google Scholar

  4. Gerald Badurek
    View author publications

    Search author on:PubMed Google Scholar

  5. Masanao Ozawa
    View author publications

    Search author on:PubMed Google Scholar

  6. Yuji Hasegawa
    View author publications

    Search author on:PubMed Google Scholar

Contributions

J.E., G.S. and S.S. carried out the experiment and analysed the data; G.B. contributed to the development at the early stage of the experiments; M.O. supplied the theoretical part and conceived the experiment; Y.H. conceived and carried out the experiment; all authors co-wrote the paper.

Corresponding author

Correspondence to Yuji Hasegawa.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Erhart, J., Sponar, S., Sulyok, G. et al. Experimental demonstration of a universally valid error–disturbance uncertainty relation in spin measurements. Nature Phys 8, 185–189 (2012). https://doi.org/10.1038/nphys2194

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys2194

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing