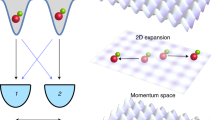
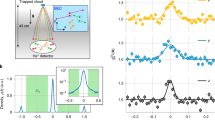
Abstract
Hanbury Brown and Twiss correlations—correlations in far-field intensity fluctuations—yield fundamental information on the quantum statistics of light sources, as demonstrated after the discovery of photon bunching1,2,3. Drawing on the analogy between photons and atoms, similar measurements have been performed for matter-wave sources, probing density fluctuations of expanding ultracold Bose gases4,5,6,7,8. Here we use two-point density correlations to study how coherence is gradually established when crossing the Bose–Einstein condensation threshold. Our experiments reveal a persistent multimode character of the emerging matter-wave as seen in the non-trivial spatial shape of the correlation functions for all probed source geometries, from nearly isotropic to quasi-one-dimensional, and for all probed temperatures. The qualitative features of our observations are captured by ideal Bose gas theory9, whereas the quantitative differences illustrate the role of particle interactions.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Hanbury Brown, R. & Twiss, R. Q. Correlation between photons in two coherent beams of light. Nature 177, 27–29 (1956).
Fano, U. Quantum theory of interference effects in the mixing of light from phase-independent sources. Am. J. Phys. 29, 539–545 (1961).
Glauber, R. J. The quantum theory of optical coherence. Phys. Rev. 130, 2529–2539 (1963).
Yasuda, M. & Shimizu, F. Observation of two-atom correlation of an ultracold neon atomic beam. Phys. Rev. Lett. 77, 3090–3093 (1996).
Fölling, S. et al. Spatial quantum noise interferometry in expanding ultracold atom clouds. Nature 434, 481–484 (2005).
Schellekens, M. et al. Hanbury Brown–Twiss effect for ultracold quantum gases. Science 310, 648–651 (2005).
Jeltes, T. et al. Comparison of the Hanbury Brown–Twiss effect for bosons and fermions. Nature 445, 402–405 (2007).
Hodgman, S. S., Dall, R. G., Manning, A. G., Baldwin, K. G. H. & Truscott, A. G. Direct measurement of long-range third-order coherence in Bose–Einstein condensates. Science 331, 1046–1049 (2011).
Viana Gomes, J. et al. Theory for a Hanbury Brown–Twiss experiment with a ballistically expanding cloud of cold atoms. Phys. Rev. A 74, 053607 (2006).
Öttl, A., Ritter, S., Köhl, M. & Esslinger, T. Correlations and counting statistics of an atom laser. Phys. Rev. Lett. 95, 090404 (2005).
Dall, R. G. et al. Observation of atomic speckle and Hanbury Brown–Twiss correlations in guided matter waves. Nature Comm. 2, 291 (2011).
Arecchi, F. T. Measurement of the statistical distribution of Gaussian and laser sources. Phys. Rev. Lett. 15, 912–916 (1965).
Bloch, I. F., Hänsch, T. W. & Esslinger, T. Measurement of the spatial coherence of a trapped Bose gas at the phase transition. Nature 403, 166–170 (2000).
Donner, T. et al. Critical behavior of a trapped interacting Bose gas. Science 315, 1556–1558 (2007).
Petrov, D. S., Shlyapnikov, G. V. & Walraven, J. T. M. Regimes of quantum degeneracy in trapped 1D gases. Phys. Rev. Lett. 85, 3745–3749 (2000).
Petrov, D. S., Shlyapnikov, G. V. & Walraven, J. T. M. Phase-fluctuating 3D Bose–Einstein condensates in elongated traps. Phys. Rev. Lett. 87, 050404 (2001).
Imambekov, A. et al. Density ripples in expanding low-dimensional gases as a probe of correlations. Phys. Rev. A 80, 033604 (2009).
Dettmer, S. et al. Observation of phase fluctuations in elongated Bose–Einstein condensates. Phys. Rev. Lett. 87, 160406 (2001).
Manz, S. et al. Two-point density correlations of quasicondensates in free expansion. Phys. Rev. A 81, 031610 (2010).
Bücker, R. et al. Single-particle-sensitive imaging of freely propagating ultracold atoms. New J. Phys. 11, 103039 (2009).
Folman, R., Krüger, P., Schmiedmayer, J., Denschlag, J. & Henkel, C. Microscopic atom optics: from wires to an atom chip. Adv. At. Mol. Phys. 48, 263–356 (2002).
Trinker, M. et al. Multilayer atom chips for versatile atom micromanipulation. Appl. Phys. Lett. 92, 254102 (2008).
Gerbier, F. Quasi-1D Bose–Einstein condensates in the dimensional crossover regime. Europhys. Lett. 66, 771–777 (2004).
Mazets, I. E., Schumm, T. & Schmiedmayer, J. Breakdown of integrability in a quasi-1d ultracold bosonic gas. Phys. Rev. Lett. 100, 210403 (2008).
Rigol, M., Dunjko, V. & Olshanii, M. Thermalization and its mechanism for generic isolated quantum systems. Nature 452, 854–858 (2008).
Mazets, I. E. & Schmiedmayer, J. Thermalization in a quasi-one-dimensional ultracold bosonic gas. New J. Phys. 12, 055023 (2010).
Davis, M. J. & Blair Blakie, P. Critical temperature of a trapped Bose gas: comparison of theory and experiment. Phys. Rev. Lett. 96, 060404 (2006).
Kheruntsyan, K., Gangardt, D. M., Drummond, P. D. & Shlyapnikov, G. V. Pair correlations in a finite-temperature 1D Bose gas. Phys. Rev. Lett. 91, 040403 (2003).
Castin, Y. & Dum, R. Bose–Einstein condensates in time dependent traps. Phys. Rev. Lett. 77, 5315–5319 (1996).
Kagan, Y., Surkov, E. L. & Shlyapnikov, G. V. Evolution of a Bose-condensed gas under variations of the confining potential. Phys. Rev. A 54, R1753–R1756 (1996).
Acknowledgements
We acknowledge support from the Wittgenstein prize, Austrian Science Fund (FWF) projects F40, P21080-N16 and P22590-N16, the European Union projects AQUTE and Marie Curie (FP7 GA no. 236702), the FWF doctoral program CoQuS (W 1210), the EUROQUASAR QuDeGPM Project and the FunMat research alliance. We wish to thank A. Aspect, D. Boiron, A. Gottlieb, I. Mazets, J. Vianna Gomes and C. I. Westbrook for stimulating discussions.
Author information
Authors and Affiliations
Contributions
A.P., R.B., S.M. and T.S. collected the data presented in this Letter. A.P. analysed the data and developed the ideal Bose gas model. All authors contributed to the building of the experimental set-up, the conceptual formulation of the physics, the interpretation of the data and writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 947 kb)
Rights and permissions
About this article
Cite this article
Perrin, A., Bücker, R., Manz, S. et al. Hanbury Brown and Twiss correlations across the Bose–Einstein condensation threshold. Nature Phys 8, 195–198 (2012). https://doi.org/10.1038/nphys2212
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/nphys2212
This article is cited by
-
Observation of the Hanbury Brown–Twiss effect with ultracold molecules
Nature Physics (2022)
-
Condensation and thermalization of an easy-plane ferromagnet in a spinor Bose gas
Nature Physics (2022)
-
On the survival of the quantum depletion of a condensate after release from a magnetic trap
Scientific Reports (2022)
-
Polariton condensation and surface enhanced Raman in spherical ZnO microcrystals
Nature Communications (2020)
-
Dependence of the Bose-Condensate Population Fluctuations in a Gas of Interacting Particles on the System Size: Numerical Analysis
Radiophysics and Quantum Electronics (2020)