Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Free randomness can be amplified

Nature Physics volume 8, pages 450–453 (2012)Cite this article

Subjects

Abstract

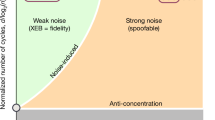
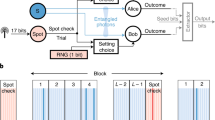
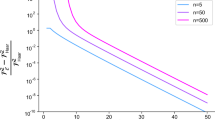
Are there fundamentally random processes in nature? Theoretical predictions, confirmed experimentally, such as the violation of Bell inequalities1, point to an affirmative answer. However, these results are based on the assumption that measurement settings can be chosen freely at random2, so assume the existence of perfectly free random processes from the outset. Here we consider a scenario in which this assumption is weakened and show that partially free random bits can be amplified to make arbitrarily free ones. More precisely, given a source of random bits whose correlation with other variables is below a certain threshold, we propose a procedure for generating fresh random bits that are virtually uncorrelated with all other variables. We also conjecture that such procedures exist for any non-trivial threshold. Our result is based solely on the no-signalling principle, which is necessary for the existence of free randomness.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Illustration of the bipartite set-up.
Figure 2: Typical causal structure of a protocol.

Similar content being viewed by others

References

  1. Bell, J. S. Speakable and Unspeakable in Quantum Mechanics Ch. 2 (Cambridge Univ. Press, 1987).

    MATH  Google Scholar 

  2. Bell, J. S. Speakable and Unspeakable in Quantum Mechanics Ch. 12 (Cambridge Univ. Press, 1987).

    MATH  Google Scholar 

  3. De Finetti, B. La prévision: Ses lois logiques, ses sources subjectives. Ann. de l’Inst. Henri Poincaré 7, 1–68 (1937).

    MATH  Google Scholar 

  4. Renner, R. Symmetry of large physical systems implies independence of subsystems. Nature Phys. 3, 645–649 (2007).

    Article  ADS  Google Scholar 

  5. Kofler, J., Paterek, T. & Brukner, C. Experimenter’s freedom in Bell’s theorem and quantum cryptography. Phys. Rev. A 73, 022104 (2006).

    Article  ADS  Google Scholar 

  6. Hall, M. J. W. Local deterministic model of singlet state correlations based on relaxing measurement independence. Phys. Rev. Lett. 105, 250404 (2010).

    Article  ADS  Google Scholar 

  7. Barrett, J. & Gisin, N. How much measurement independence is needed to demonstrate nonlocality? Phys. Rev. Lett. 106, 100406 (2011).

    Article  ADS  Google Scholar 

  8. Hall, M. J. W. Relaxed Bell inequalities and Kochen-Specker theorems. Phys. Rev. A 84, 022102 (2011).

    Article  ADS  Google Scholar 

  9. Lorenzo, A. D. Free will and quantum mechanics. Preprint at http://arxiv.org/abs/1105.1134 (2011).

  10. Pearle, P. M. Hidden-variable example based upon data rejection. Phys. Rev. D 2, 1418–1425 (1970).

    Article  ADS  Google Scholar 

  11. Braunstein, S. L. & Caves, C. M. Wringing out better Bell inequalities. Ann. Phys. 202, 22–56 (1990).

    Article  ADS  MATH  Google Scholar 

  12. Colbeck, R. & Renner, R. No extension of quantum theory can have improved predictive power. Nature Commun. 2, 411 (2011).

    Article  ADS  Google Scholar 

  13. Barrett, J., Hardy, L. & Kent, A. No signalling and quantum key distribution. Phys. Rev. Lett. 95, 010503 (2005).

    Article  ADS  Google Scholar 

  14. Conway, J. & Kochen, S. The free will theorem. Found. Phys. 36, 1441–1473 (2006).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. Conway, J. H. & Kochen, S. The strong free will theorem. Notices AMS 56, 226–232 (2009).

    MathSciNet  MATH  Google Scholar 

  16. Santha, M. & Vazirani, U. V. in Proc. 25th IEEE Symposium on Foundations of Computer Science (FOCS-84) 434–440 (IEEE Computer Society, 1984).

    Google Scholar 

  17. Colbeck, R. Quantum and Relativistic Protocols For Secure Multi-Party Computation PhD thesis, Univ. Cambridge (2007); available at http://arxiv.org/abs/0911.3814.

  18. Pironio, S. et al. Random numbers certified by Bell’s theorem. Nature 464, 1021–1024 (2010).

    Article  ADS  Google Scholar 

  19. Colbeck, R. & Kent, A. Private randomness expansion with untrusted devices. J. Phys. A 44, 095305 (2011).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  20. De, A., Portmann, C., Vidick, T. & Renner, R. Trevisan’s extractor in the presence of quantum side information. Preprint at http://arxiv.org/abs/0912.5514 (2009).

  21. Trevisan, L. Extractors and pseudorandom generators. J. ACM 48, 860–879 (2001).

    Article  MathSciNet  MATH  Google Scholar 

  22. Scheidl, T. et al. Violation of local realism with freedom of choice. Proc. Natl Acad. Sci. USA 107, 19708 (2010).

    Article  ADS  MATH  Google Scholar 

  23. Dodis, Y., Ong, S. J., Prabhakaran, M. & Sahai, A. in Proc. 45th Annual IEEE Symposium on Foundations of Computer Science (FOCS-04) 196–205 (Lecture Notes in Computer Science, IEEE Computer Society, 2004).

    Book  Google Scholar 

  24. Barrett, J., Kent, A. & Pironio, S. Maximally non-local and monogamous quantum correlations. Phys. Rev. Lett. 97, 170409 (2006).

    Article  ADS  Google Scholar 

  25. Colbeck, R. & Renner, R. Hidden variable models for quantum theory cannot have any local part. Phys. Rev. Lett. 101, 050403 (2008).

    Article  ADS  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We thank V. Galliard for useful discussions and L. del Rio for the figures. Research at Perimeter Institute is supported by the Government of Canada through Industry Canada and by the Province of Ontario through the Ministry of Research and Innovation. R.R. acknowledges support from the Swiss National Science Foundation (grant No 200020-135048, the National Centre of Competence in Research QSIT and the CHIST-ERA project DIQIP) and from the European Research Council (grant No 258932).

Author information

Authors and Affiliations

  1. Institute for Theoretical Physics, ETH Zurich, 8093 Zurich, Switzerland

    Roger Colbeck & Renato Renner

  2. Perimeter Institute for Theoretical Physics, 31 Caroline Street North, Waterloo, Ontario N2L 2Y5, Canada

    Roger Colbeck

Authors
  1. Roger Colbeck
    View author publications

    Search author on:PubMed Google Scholar

  2. Renato Renner
    View author publications

    Search author on:PubMed Google Scholar

Contributions

Both authors contributed equally to this work.

Corresponding author

Correspondence to Roger Colbeck.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 549 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Colbeck, R., Renner, R. Free randomness can be amplified. Nature Phys 8, 450–453 (2012). https://doi.org/10.1038/nphys2300

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys2300

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing