Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Experimental estimation of the dimension of classical and quantum systems

Nature Physics volume 8, pages 588–591 (2012)Cite this article

Subjects

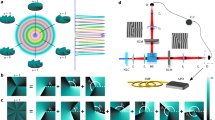
Abstract

Experimental observations are usually described using theoretical models that make assumptions about the dimensionality of the system under consideration. However, would it be possible to assess the dimension of a completely unknown system only from the results of measurements performed on it, without any extra assumption? The concept of a dimension witness1,2,3,4,5,6 answers this question, as it allows bounding the dimension of an unknown system only from measurement statistics. Here, we report on the experimental demonstration of dimension witnesses in a prepare and measure scenario6. We use photon pairs entangled in polarization and orbital angular momentum 7,8,9 to generate ensembles of classical and quantum states of dimensions up to 4. We then use a dimension witness to certify their dimensionality as well as their quantum nature. Our work opens new avenues in quantum information science, where dimension represents a powerful resource10,11,12, especially for device-independent estimation of quantum systems13,14,15,16 and quantum communications17,18.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Sketch of a device-independent test of the dimension of an ensemble of states.
Figure 2: Experimental set-up.
Figure 3: Dimension witness I4 for qubit (blue triangles), qutrit (red circles) and quart (green diamonds) states as a function of temporal delay τ.

Similar content being viewed by others

References

  1. Brunner, N., Pironio, S., Acín, A., Gisin, N., Méthot, A. & Scarani, V. Testing the dimension of Hilbert spaces. Phys. Rev. Lett. 100, 210503 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  2. Pál, K. & Vértesi, T. Efficiency of higher-dimensional Hilbert spaces for the violation of Bell inequalities. Phys. Rev. A 77, 042105 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  3. Pérez-García, D., Wolf, M. M., Palazuelos, C., Villanueva, I. & Junge, M. Unbounded violation of tripartite Bell inequalities. Commun. Math. Phys. 279, 455–486 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  4. Wehner, S., Christandl, M. & Doherty, A. C. Lower bound on the dimension of a quantum system given measured data. Phys. Rev. A 78, 062112 (2008).

    Article  ADS  Google Scholar 

  5. Wolf, M. M. & Pérez-García, D. Assessing quantum dimensionality from observable dynamics. Phys. Rev. Lett. 102, 190504 (2009).

    Article  ADS  MathSciNet  Google Scholar 

  6. Gallego, R., Brunner, N., Hadley, C. & Acín, A. Device-independent tests of classical and quantum dimensions. Phys. Rev. Lett. 105, 230501 (2010).

    Article  ADS  Google Scholar 

  7. Molina-Terriza, G., Torres, J. P. & Torner, L. Twisted photons. Nature Phys. 3, 305–310 (2007).

    Article  ADS  Google Scholar 

  8. Mair, A., Vaziri, A., Weihs, G. & Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 412, 313–316 (2001).

    Article  ADS  Google Scholar 

  9. Dada, A. C., Leach, J., Buller, G. S., Padgett, M. J. & Andersson, E. Experimental high-dimensional two-photon entanglement and violations of generalized Bell inequalities. Nature Phys. 7, 677–680 (2011).

    Article  ADS  Google Scholar 

  10. Lanyon, B. et al. Simplifying quantum logic using higher-dimensional Hilbert spaces. Nature Phys. 5, 134–140 (2009).

    Article  ADS  Google Scholar 

  11. Spekkens, R. W. & Rudolph, T. Degrees of concealment and bindingness in quantum bit commitment protocols. Phys. Rev. A 65, 012310 (2001).

    Article  ADS  Google Scholar 

  12. Acín, A., Gisin, N. & Masanes, Ll. From Bell’s theorem to secure quantum key distribution. Phys. Rev. Lett. 97, 120405 (2006).

    Article  ADS  Google Scholar 

  13. Mayers, D. & Yao, A. Self testing quantum apparatus. Quant. Inf. Comp. 4, 273–286 (2004).

    MathSciNet  MATH  Google Scholar 

  14. Bardyn, C.-E., Liew, T. C. H., Massar, S., McKague, M. & Scarani, V. Device-independent state estimation based on Bell’s inequalities. Phys. Rev. A 80, 062327 (2009).

    Article  ADS  Google Scholar 

  15. Bancal, J-D., Gisin, N., Liang, Y-C. & Pironio, S. Device-independent witnesses of genuine multipartite entanglement. Phys. Rev. Lett. 106, 250404 (2011).

    Article  ADS  Google Scholar 

  16. Rabelo, R., Ho, M., Cavalcanti, D., Brunner, N. & Scarani, V. Device-independent certification of entangled measurements. Phys. Rev. Lett. 107, 050502 (2011).

    Article  ADS  Google Scholar 

  17. Pawlowski, M. & Brunner, N. Semi-device-independent security of one-way quantum key distribution. Phys. Rev. A 84, 010302 (2011).

    Article  ADS  Google Scholar 

  18. Li, H-W. et al. Semi-device-independent random-number expansion without entanglement. Phys. Rev. A 84, 034301 (2011).

    Article  ADS  Google Scholar 

  19. Langford, N. K. et al. Measuring entangled qutrits and their use for quantum bit commitment. Phys. Rev. Lett. 93, 053601 (2004).

    Article  ADS  Google Scholar 

  20. Molina-Terriza, G., Vaziri, A., Ursin, R. & Zeilinger, A. Experimental Quantum Coin Tossing. Phys. Rev. Lett. 94, 040501 (2005).

    Article  ADS  Google Scholar 

  21. Massar, S. Nonlocality, closing the detection loophole, and communication complexity. Phys. Rev. A 65, 032121 (2002).

    Article  ADS  Google Scholar 

  22. Vértesi, T., Pironio, S. & Brunner, N. Closing the detection loophole in bell experiments using qudits. Phys. Rev. Lett. 104, 060401 (2010).

    Article  ADS  Google Scholar 

  23. Vértesi, T. & Pál, K. Generalized Clauser-Horne-Shimony-Holt inequalities maximally violated by higher-dimensional systems. Phys. Rev. A 77, 042106 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  24. Junge, M., Palazuelos, C., Pérez-García, D., Villanueva, I. & Wolf, M. M. Operator space theory: A natural framework for bell inequalities. Phys. Rev. Lett. 104, 170405 (2010).

    Article  ADS  MathSciNet  Google Scholar 

  25. Briët, J., Buhrman, H. & Toner, B. A generalized Grothendieck inequality and nonlocal correlations that require high entanglement. Commun. Math. Phys. 305, 827–843 (2011).

    Article  ADS  MathSciNet  Google Scholar 

  26. Junge, M. & Palazuelos, C. Large violation of Bell inequalities with low entanglement. Commun. Math. Phys. 306, 695–746 (2011).

    Article  ADS  MathSciNet  Google Scholar 

  27. Molina-Terriza, G., Torres, J. P. & Torner, L. Management of the orbital angular momentum of light: Preparation of photons in multidimensional vector states of angular momentum. Phys. Rev. Lett. 88, 013601 (2002).

    Article  ADS  Google Scholar 

  28. Allen, L., Beijersbergen, M. W., Spreeuw, R. J. C. & Woerdman, J. P. Orbital angular momentum of light and the transformation of Laguerre–Gaussian laser modes. Phys. Rev. A 45, 8185–8189 (1992).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank C. Hadley and E. Nagali for contributions in early stages of this work. We acknowledge support from the ERC Starting Grant PERCENT, the EU Projects Q-Essence, QCS and PHORBITECH (FET OPEN grant number 255914), the UK EPSRC, the Project MSM6198959213 of the Czech Ministry of Education, the Spanish projects FIS2010-14830, FIS2010-14831 and Chist-Era DIQIP, an FI Grant of the Generalitat de Catalunya, CatalunyaCaixa, and Fundació Privada Cellex, Barcelona.

Author information

Authors and Affiliations

  1. ICFO-Institut de Ciencies Fotoniques, 08860 Castelldefels (Barcelona), Spain

    Martin Hendrych, Rodrigo Gallego, Michal Mičuda, Antonio Acín & Juan P. Torres

  2. Department of Optics, Palacký University, 77146 Olomouc, 17. listopadu 12, Czech Republic

    Michal Mičuda

  3. H.H. Wills Physics Laboratory, University of Bristol, Bristol BS8 1TL, UK

    Nicolas Brunner

  4. ICREA-Institució Catalana de Recerca i Estudis Avançats, 08010 Barcelona, Spain

    Antonio Acín

  5. Department of Signal Theory and Communications, Universitat Politècnica de Catalunya, 08034 Barcelona, Spain

    Juan P. Torres

Authors
  1. Martin Hendrych
    View author publications

    Search author on:PubMed Google Scholar

  2. Rodrigo Gallego
    View author publications

    Search author on:PubMed Google Scholar

  3. Michal Mičuda
    View author publications

    Search author on:PubMed Google Scholar

  4. Nicolas Brunner
    View author publications

    Search author on:PubMed Google Scholar

  5. Antonio Acín
    View author publications

    Search author on:PubMed Google Scholar

  6. Juan P. Torres
    View author publications

    Search author on:PubMed Google Scholar

Contributions

R.G., N.B. and A.A. developed the theory, M.H., R.G., N.B., A.A. and J.P.T. designed the experiment, and M.H., M.M. and J.P.T. performed the experiment. All of the authors contributed to the writing of the manuscript.

Corresponding authors

Correspondence to Antonio Acín or Juan P. Torres.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 473 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hendrych, M., Gallego, R., Mičuda, M. et al. Experimental estimation of the dimension of classical and quantum systems. Nature Phys 8, 588–591 (2012). https://doi.org/10.1038/nphys2334

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys2334

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing