Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

A superheated Bose-condensed gas

Nature Physics volume 9, pages 271–274 (2013)Cite this article

Subjects

This article has been updated

Abstract

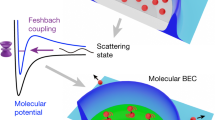
Our understanding of various states of matter usually relies on the assumption of thermodynamic equilibrium. However, the transitions between different phases of matter can be strongly affected by non-equilibrium phenomena. Here we demonstrate and explain an example of non-equilibrium stalling of a continuous, second-order phase transition. We create a superheated atomic Bose gas, in which a Bose–Einstein condensate (BEC) persists above the equilibrium critical temperature1,2, Tc, if its coupling to the surrounding thermal bath is reduced by tuning interatomic interactions. For vanishing interactions the BEC persists in the superheated regime for a minute. However, if strong interactions are suddenly turned on, it rapidly boils away. Our observations can be understood within a two-fluid picture, treating the condensed and thermal components of the gas as separate equilibrium systems with a tunable inter-component coupling. We experimentally reconstruct a non-equilibrium phase diagram of our gas, and theoretically reproduce its main features.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Creating and understanding a superheated Bose-condensed gas.
Figure 2: Equilibrium versus non-equilibrium BEC decay.
Figure 3: Quenching the superheated Bose-condensed gas.
Figure 4: Limits of superheating.

Similar content being viewed by others

Change history

  • 28 March 2013

    In the version of this Letter originally published online, in Fig. 3, the orange shading indicating the superheated region should have extended to the right-hand edge of the figure. This error has now been corrected in all versions of the Letter.

References

  1. Dalfovo, F., Giorgini, S., Pitaevskii, L. P. & Stringari, S. Theory of Bose–Einstein condensation in trapped gases. Rev. Mod. Phys. 71, 463–512 (1999).

    Article  ADS  Google Scholar 

  2. Smith, R. P., Campbell, R. L. D., Tammuz, N. & Hadzibabic, Z. Effects of interactions on the critical temperature of a trapped Bose gas. Phys. Rev. Lett. 106, 250403 (2011).

    Article  ADS  Google Scholar 

  3. Polkovnikov, A., Sengupta, K., Silva, A. & Vengalattore, M. Colloquium: Nonequilibrium dynamics of closed interacting quantum systems. Rev. Mod. Phys. 83, 863–883 (2011).

    ADS  Google Scholar 

  4. Kinoshita, T., Wenger, T. & Weiss, D. S. A quantum Newton’s cradle. Nature 440, 900–903 (2006).

    Article  ADS  Google Scholar 

  5. Winkler, K. et al. Repulsively bound atom pairs in an optical lattice. Nature 441, 853–856 (2006).

    Article  ADS  Google Scholar 

  6. Sadler, L. E., Higbie, J. M., Leslie, S. R., Vengalattore, M. & Stamper-Kurn, D. M. Spontaneous symmetry breaking in a quenched ferromagnetic spinor Bose–Einstein condensate. Nature 443, 312–315 (2006).

    Article  ADS  Google Scholar 

  7. Hofferberth, S., Lesanovsky, I., Fischer, B., Schumm, T. & Schmiedmayer, J. Non-equilibrium coherence dynamics in one-dimensional Bose gases. Nature 449, 324–327 (2007).

    Article  ADS  Google Scholar 

  8. Haller, E. et al. Realization of an excited, strongly correlated quantum gas phase. Science 325, 1224–1227 (2009).

    Article  ADS  Google Scholar 

  9. Guzman, J. et al. Long-time-scale dynamics of spin textures in a degenerate F = 1 87Rb spinor Bose gas. Phys. Rev. A 84, 063625 (2011).

    Article  ADS  Google Scholar 

  10. Cheneau, M. et al. Light-cone-like spreading of correlations in a quantum many-body system. Nature 481, 484–487 (2012).

    Article  ADS  Google Scholar 

  11. Trotzky, S. et al. Probing the relaxation towards equilibrium in an isolated strongly correlated one-dimensional Bose gas. Nature Phys. 8, 325–330 (2012).

    Article  ADS  Google Scholar 

  12. Mark, M. J. et al. Preparation and spectroscopy of a metastable Mott-insulator state with attractive interactions. Phys. Rev. Lett. 108, 215302 (2012).

    Article  ADS  Google Scholar 

  13. Smith, R. P., Beattie, S., Moulder, S., Campbell, R. L. D. & Hadzibabic, Z. Condensation dynamics in a quantum-quenched Bose gas. Phys. Rev. Lett. 109, 105301 (2012).

    Article  ADS  Google Scholar 

  14. Gring, M. et al. Relaxation and pre-thermalization in an isolated quantum system. Science 337, 1318–1322 (2012).

    Article  ADS  Google Scholar 

  15. Mathey, L. & Polkovnikov, A. Light cone dynamics and reverse Kibble–Zurek mechanism in two-dimensional superfluids following a quantum quench. Phys. Rev. A 81, 033605 (2010).

    Article  ADS  Google Scholar 

  16. Fedichev, P. O., Shlyapnikov, G. V. & Walraven, J. T. M. Damping of low-energy excitations of a trapped Bose–Einstein condensate at finite temperatures. Phys. Rev. Lett. 80, 2269–2272 (1998).

    Article  ADS  Google Scholar 

  17. Pethick, C. & Smith, H. Bose–Einstein Condensation in Dilute Gases (Cambridge Univ. Press, 2002).

    Google Scholar 

  18. Campbell, R. L. D. et al. Efficient production of large 39K Bose–Einstein condensates. Phys. Rev. A 82, 063611 (2010).

    Article  ADS  Google Scholar 

  19. Roati, G. et al. 39K Bose–Einstein condensate with tunable interactions. Phys. Rev. Lett. 99, 010403 (2007).

    Article  ADS  Google Scholar 

  20. Tammuz, N. et al. Can a Bose gas be saturated? Phys. Rev. Lett. 106, 230401 (2011).

    Article  ADS  Google Scholar 

  21. Smith, R. P. & Hadzibabic, Z. Effects of interactions on Bose–Einstein condensation of an atomic gas. Preprint at http://arxiv.org/abs/1203.2063 (2012).

  22. Ruprecht, P. A., Holland, M. J., Burnett, K. & Edwards, M. Time-dependent solution of the nonlinear Schrödinger equation for Bose-condensed trapped neutral atoms.Phys. Rev. A 51, 4704–4711 (1995).

    Article  ADS  Google Scholar 

  23. Gerton, J. M., Strekalov, D., Prodan, I. & Hulet, R. G. Direct observation of growth and collapse of a Bose–Einstein condensate with attractive interactions. Nature 408, 692–695 (2000).

    Article  ADS  Google Scholar 

  24. Donley, E. A. et al. Dynamics of collapsing and exploding Bose–Einstein condensates. Nature 412, 295–299 (2001).

    Article  ADS  Google Scholar 

  25. Gardiner, C. W., Zoller, P., Ballagh, R. J. & Davis, M. J. Kinetics of Bose–Einstein condensation in a trap. Phys. Rev. Lett. 79, 1793–1796 (1997).

    Article  ADS  Google Scholar 

  26. Gardiner, C. W., Lee, M. D., Ballagh, R. J., Davis, M. J. & Zoller, P. Quantum kinetic theory of condensate growth: Comparison of experiment and theory. Phys. Rev. Lett. 81, 5266–5269 (1998).

    Article  ADS  Google Scholar 

  27. Smith, R. P., Tammuz, N., Campbell, R. L. D., Holzmann, M. & Hadzibabic, Z. Condensed fraction of an atomic Bose gas induced by critical correlations. Phys. Rev. Lett. 107, 190403 (2011).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank S. Beattie and S. Moulder for experimental assistance. This work was supported by EPSRC (Grant No. EP/K003615/1), the Royal Society, AFOSR, ARO and DARPA OLE.

Author information

Author notes

  1. Alexander L. Gaunt and Richard J. Fletcher: These authors contributed equally to this work

Authors and Affiliations

  1. Cavendish Laboratory, University of Cambridge, J. J. Thomson Avenue, Cambridge CB3 0HE, UK

    Alexander L. Gaunt, Richard J. Fletcher, Robert P. Smith & Zoran Hadzibabic

Authors
  1. Alexander L. Gaunt
    View author publications

    Search author on:PubMed Google Scholar

  2. Richard J. Fletcher
    View author publications

    Search author on:PubMed Google Scholar

  3. Robert P. Smith
    View author publications

    Search author on:PubMed Google Scholar

  4. Zoran Hadzibabic
    View author publications

    Search author on:PubMed Google Scholar

Contributions

All authors contributed extensively to this work.

Corresponding author

Correspondence to Robert P. Smith.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 363 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gaunt, A., Fletcher, R., Smith, R. et al. A superheated Bose-condensed gas. Nature Phys 9, 271–274 (2013). https://doi.org/10.1038/nphys2587

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys2587

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing