Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Long-range orientational order in two-dimensional microfluidic dipoles

Nature Physics volume 10, pages 140–144 (2014)Cite this article

Subjects

Abstract

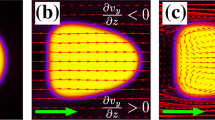
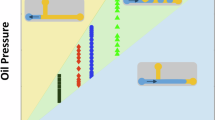
Dynamic restructuring and ordering are prevalent in driven many-body systems with long-range interactions, such as sedimenting particles1,2,3, dusty plasmas4, flocking animals5,6,7 and microfluidic droplets8. Yet, understanding such collective dynamics from basic principles is challenging because these systems are not governed by global minimization principles, and because every constituent interacts with many others. Here, we report long-range orientational order of droplet velocities in disordered two-dimensional microfluidic droplet ensembles. Droplet velocities exhibit strong long-range correlation as 1/r2, with a four-fold angular symmetry. The two-droplet correlation can be explained by representing the entire ensemble as a third droplet. The correlation amplitude is non-monotonous with density owing to excluded-volume effects. Our study puts forth a many-body problem with long-range interactions that is solvable from first principles owing to the reduced dimensionality, and introduces new experimental tools to address open problems in many-body non-equilibrium systems9,10.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: The microfluidic 2D droplet ensemble and velocity fluctuations.
Figure 2: Velocity correlations.
Figure 3: Velocity variance determined by competition of single- and dual-droplet effects.

Similar content being viewed by others

References

  1. Segrè, P. N., Herbolzheimer, E. & Chaikin, P. M. Long-range correlations in sedimentation. Phys. Rev. Lett. 79, 2574–2577 (1997).

    Article  ADS  Google Scholar 

  2. Segrè, P. N., Liu, F., Umbanhowar, P. & Weitz, D. A. An effective gravitational temperature for sedimentation. Nature 409, 594–597 (2001).

    Article  ADS  Google Scholar 

  3. Mucha, P. J., Tee, S-Y., Weitz, D. A., Shraiman, B. I. & Brenner, M. P. A model for velocity fluctuations in sedimentation. J. Fluid Mech. 501, 71–104 (2004).

    Article  ADS  MathSciNet  Google Scholar 

  4. Morfill, G. E. & Ivlev, A. V. Complex plasmas: An interdisciplinary research field. Rev. Mod. Phys. 81, 1353–1404 (2009).

    Article  ADS  Google Scholar 

  5. Toner, J., Tu, Y. & Ramaswamy, S. Hydrodynamics and phases of flocks. Ann. Phys. 318, 170–244 (2005).

    Article  ADS  MathSciNet  Google Scholar 

  6. Zhang, H. & Be’er, A. Collective motion and density fluctuations in bacterial colonies. Proc. Natl Acad. Sci. USA 107, 13626–13630 (2010).

    Article  ADS  Google Scholar 

  7. Cavagna, A. et al. Scale-free correlations in starling flocks. Proc. Natl Acad. Sci. USA 107, 11865–11870 (2010).

    Article  ADS  Google Scholar 

  8. Beatus, T., Tlusty, T. & Bar-Ziv, R. Phonons in a one-dimensional microfluidic crystal. Nature Phys. 2, 743–748 (2006).

    Article  ADS  Google Scholar 

  9. Campa, A., Dauxois, T. & Ruffo, S. Statistical mechanics and dynamics of solvable models with long-range interactions. Phys. Rep. 480, 57–159 (2009).

    Article  ADS  MathSciNet  Google Scholar 

  10. Bouchet, F. & Barré, J. Statistical mechanics of systems with long range interactions. J. Phys. Conf. Ser. 31, 18–26 (2006).

    Article  ADS  Google Scholar 

  11. Cui, B., Diamant, H., Lin, B. & Rice, S. Anomalous hydrodynamic interaction in a quasi-two-dimensional suspension. Phys. Rev. Lett. 92, 258301 (2004).

    Article  ADS  Google Scholar 

  12. Rouyer, F., Lhuillier, D., Martin, J. & Salin, D. Structure, density, and velocity fluctuations in quasi-two-dimensional non-Brownian suspensions of spheres. Phys. Fluids 12, 958–963 (2000).

    Article  ADS  MathSciNet  Google Scholar 

  13. Long, D., Stone, H. A. & Ajdari, A. Electroosmotic flows created by surface defects in capillary electrophoresis. J. Colloid Interface Sci. 212, 338–349 (1999).

    Article  ADS  Google Scholar 

  14. Suzuki, Y. Y. & Izuyama, T. Diffusion of molecules in biomembranes. J. Phys. Soc. Jpn 58, 1104–1119 (1989).

    Article  ADS  Google Scholar 

  15. Thorsen, T., Roberts, R. W., Arnold, F. H. & Quake, S. R. Dynamic pattern formation in a vesicle-generating microfluidic device. Phys. Rev. Lett. 86, 4163–4166 (2001).

    Article  ADS  Google Scholar 

  16. Beatus, T., Bar-Ziv, R. H. & Tlusty, T. The physics of 2D microfluidic droplet ensembles. Phys. Rep. 516, 103–145 (2012).

    Article  ADS  Google Scholar 

  17. Landau, L. D., Lifshitz, E. M. & Pitaevskii, L. P. Electrodynamics of continuous media. Course Theor. Phys. 8, 45–47 (1984).

    Google Scholar 

  18. Beatus, T., Bar-Ziv, R. & Tlusty, T. Anomalous microfluidic phonons induced by the interplay of hydrodynamic screening and incompressibility. Phys. Rev. Lett. 99, 124502 (2007).

    Article  ADS  Google Scholar 

  19. Baron, M., Bławzdziewicz, J. & Wajnryb, E. Hydrodynamic crystals: Collective dynamics of regular arrays of spherical particles in a parallel-wall channel. Phys. Rev. Lett. 100, 174502 (2008).

    Article  ADS  Google Scholar 

  20. Beatus, T., Tlusty, T. & Bar-Ziv, R. Burgers shock waves and sound in a 2D microfluidic droplets ensemble. Phys. Rev. Lett. 103, 114502 (2009).

    Article  ADS  Google Scholar 

  21. Champagne, N., Vasseur, R., Montourcy, A. & Bartolo, D. Traffic jams and intermittent flows in microfluidic networks. Phys. Rev. Lett. 105, 044502 (2010).

    Article  ADS  Google Scholar 

  22. Champagne, N., Lauga, E. & Bartolo, D. Stability and non-linear response of 1D microfluidic-particle streams. Soft Matter 7, 11082–11085 (2011).

    Article  ADS  Google Scholar 

  23. Uspal, W. E. & Doyle, P. S. Scattering and nonlinear bound states of hydrodynamically coupled particles in a narrow channel. Phys. Rev. E 85, 016325 (2012).

    Article  ADS  Google Scholar 

  24. Desreumaux, N., Caussin, J-B., Jeanneret, R., Lauga, E. & Bartolo, D. Hydrodynamic fluctuations in confined particle-laden fluids. Phys. Rev. Lett. 111, 118301 (2013).

    Article  ADS  Google Scholar 

  25. Uspal, W. E., Burak Eral, H. & Doyle, P. S. Engineering particle trajectories in microfluidic flows using particle shape. Nature Commun. 4, 2666 (2013).

    Article  ADS  Google Scholar 

  26. Snabre, P., Pouligny, B., Metayer, C. & Nadal, F. Size segregation and particle velocity fluctuations in settling concentrated suspensions. Rheol. Acta 48, 855–870 (2009).

    Article  Google Scholar 

  27. Brotto, T., Caussin, J-B., Lauga, E. & Bartolo, D. Hydrodynamics of confined active fluids. Phys. Rev. Lett. 110, 038101 (2013).

    Article  ADS  Google Scholar 

  28. Palacci, J., Sacanna, S., Steinberg, A. P., Pine, D. J. & Chaikin, P. M. Living crystals of light-activated colloidal surfers. Science 339, 936–40 (2013).

    Article  ADS  Google Scholar 

  29. Theberge, A. B. et al. Microdroplets in microfluidics: An evolving platform for discoveries in chemistry and biology. Angew. Chem. Int. Ed. Engl. 49, 5846–68 (2010).

    Article  Google Scholar 

  30. Joensson, H. N. & Andersson Svahn, H. Droplet microfluidics—a tool for single-cell analysis. Angew. Chem. Int. Ed. Engl. 51, 12176–92 (2012).

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by a Yeda-Sela Grant (R.H.B-Z). T.B. was supported by the Cross Disciplinary Postdoctoral Fellowship of the Human Frontier Science Program. T.T. is the Helen and Martin Chooljian Founders Circle Member in the Simons Center for Systems Biology of the Institute for Advanced Study, Princeton.

Author information

Author notes

  1. Department of Physics, Cornell University, Ithaca, New York 14853, USA

Authors and Affiliations

  1. Department of Materials and Interfaces, Weizmann Institute of Science, Rehovot, Weizmann 76100, Israel

    Itamar Shani, Tsevi Beatus & Roy H. Bar-Ziv

  2. Simons Center for Systems Biology, Institute for Advanced Study, Princeton, New Jersey 08540, USA

    Tsvi Tlusty

Authors
  1. Itamar Shani
    View author publications

    Search author on:PubMed Google Scholar

  2. Tsevi Beatus
    View author publications

    Search author on:PubMed Google Scholar

  3. Roy H. Bar-Ziv
    View author publications

    Search author on:PubMed Google Scholar

  4. Tsvi Tlusty
    View author publications

    Search author on:PubMed Google Scholar

Contributions

All authors contributed to all aspects of this work.

Corresponding authors

Correspondence to Tsevi Beatus, Roy H. Bar-Ziv or Tsvi Tlusty.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 789 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Shani, I., Beatus, T., Bar-Ziv, R. et al. Long-range orientational order in two-dimensional microfluidic dipoles. Nature Phys 10, 140–144 (2014). https://doi.org/10.1038/nphys2843

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys2843

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing