Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Experimental noise filtering by quantum control

Nature Physics volume 10, pages 825–829 (2014)Cite this article

Subjects

Abstract

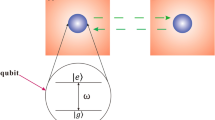
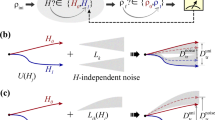
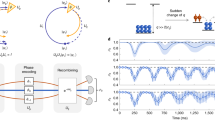
Extrinsic interference is routinely faced in systems engineering, and a common solution is to rely on a broad class of filtering techniques to afford stability to intrinsically unstable systems or isolate particular signals from a noisy background. Experimentalists leading the development of a new generation of quantum-enabled technologies similarly encounter time-varying noise in realistic laboratory settings. They face substantial challenges in either suppressing such noise for high-fidelity quantum operations1 or controllably exploiting it in quantum-enhanced sensing2,3,4 or system identification tasks 5,6, due to a lack of efficient, validated approaches to understanding and predicting quantum dynamics in the presence of realistic time-varying noise. In this work we use the theory of quantum control engineering7,8 and experiments with trapped 171Yb+ ions to study the dynamics of controlled quantum systems. Our results provide the first experimental validation of generalized filter-transfer functions casting arbitrary quantum control operations on qubits as noise spectral filters9,10. We demonstrate the utility of these constructs for directly predicting the evolution of a quantum state in a realistic noisy environment as well as for developing novel robust control and sensing protocols. These experiments provide a significant advance in our understanding of the physics underlying controlled quantum dynamics, and unlock new capabilities for the emerging field of quantum systems engineering.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Noise filters and experimental validation of the predictive power of the filter-transfer function.
Figure 2: Synthesis of high-pass amplitude-modulated filters from the Walsh functions.
Figure 3: Construction of the first-order Walsh amplitude-modulated dephasing-suppressing filter.

Similar content being viewed by others

References

  1. Smith, A. et al. Quantum control in the 6Cs1/2 ground manifold using radio-frequency and microwave magnetic fields. Phys. Rev. Lett. 111, 170502 (2013).

    Article  ADS  Google Scholar 

  2. Dolde, F. et al. Electric-field sensing using single diamond spins. Nature Phys. 7, 459–463 (2011).

    Article  ADS  Google Scholar 

  3. Kucsko, G. et al. Nanometre-scale thermometry in a living cell. Nature 500, 54–58 (2013).

    Article  ADS  Google Scholar 

  4. Cooper, A., Magesan, E., Yum, H. & Cappellaro, P. Time-resolved magnetic sensing with electronic spins in diamond. Nature Commun. 5, 3141 (2014).

    Article  ADS  Google Scholar 

  5. Álvarez, G. A. & Suter, D. Measuring the spectrum of colored noise by dynamical decoupling. Phys. Rev. Lett. 107, 230501 (2011).

    Article  ADS  Google Scholar 

  6. Bylander, J. et al. Noise spectroscopy through dynamical decoupling with a superconducting flux qubit. Nature Phys. 7, 565–570 (2011).

    Article  ADS  Google Scholar 

  7. Clark, J. W., Lucarelli, D. G. & Tarn, T. J. Control of quantum systems. Int. J. Mod. Phys. B 17, 5397–5411 (2003).

    Article  ADS  Google Scholar 

  8. Bouten, L., Handel, R. V. & James, M. R. An introduction to quantum filtering. SIAM J. Control Optim. 46, 2199–2241 (2007).

    Article  MathSciNet  Google Scholar 

  9. Green, T. J., Uys, H. & Biercuk, M. J. High-order noise filtering in nontrivial quantum logic gates. Phys. Rev. Lett. 109, 020501 (2012).

    Article  ADS  Google Scholar 

  10. Green, T. J., Sastrawan, J., Uys, H. & Biercuk, M. J. Arbitrary quantum control of qubits in the presence of universal noise. New J. Phys. 15, 095004 (2013).

    Article  ADS  Google Scholar 

  11. Kofman, A. & Kurizki, G. Universal dynamical control of quantum mechanical decay: Modulation of the coupling to the continuum. Phys. Rev. Lett. 87, 270405 (2001).

    Article  Google Scholar 

  12. Uhrig, G. Keeping a quantum bit alive by optimized pi-pulse sequences. Phys. Rev. Lett. 98, 100504 (2007).

    Article  ADS  Google Scholar 

  13. Cywinski, L., Lutchyn, R. M., Nave, C. P. & Sarma, S. D. How to enhance dephasing time in superconducting qubits. Phys. Rev. B 77, 174509 (2008).

    Article  ADS  Google Scholar 

  14. Biercuk, M. J., Doherty, A. C. & Uys, H. Dynamical decoupling sequence construction as a filter-design problem. J. Phys. B 44, 154002 (2011).

    Article  ADS  Google Scholar 

  15. Biercuk, M. J. et al. Optimized dynamical decoupling in a model quantum memory. Nature 458, 996–1000 (2009).

    Article  ADS  Google Scholar 

  16. Soare, A. et al. Experimental bath engineering for quantitative studies of quantum control. Phys. Rev. A 89, 042329 (2014).

    Article  ADS  Google Scholar 

  17. Vandersypen, L. M. K. & Chuang, I. NMR techniques for quantum control and computation. Rev. Mod. Phys. 76, 1037–1069 (2004).

    Article  ADS  Google Scholar 

  18. Merrill, J. T. & Brown, K. R. in Quantum Information and Computation for Chemistry: Advances in Chemical Physics Vol. 154 (ed. Kais, S.) Ch. 10, 241–294 (John Wiley, 2014).

    Book  Google Scholar 

  19. Kabytayev, C. et al. Robustness of composite pulses to time-dependent control noise. Phys. Rev. A 90, 012316 (2014).

    Article  ADS  Google Scholar 

  20. Haeberlen, U. & Waugh, J. S. Coherent averaging effects in magnetic resonance. Phys. Rev. 175, 453–467 (1968).

    Article  ADS  Google Scholar 

  21. Khodjasteh, K. & Viola, L. Dynamically error-corrected gates for universal quantum computation. Phys. Rev. Lett. 102, 80501 (2009).

    Article  ADS  Google Scholar 

  22. Wang, X. et al. Composite pulses for robust universal control of singlet–triplet qubits. Nature Commun. 3, 997 (2012).

    Article  ADS  Google Scholar 

  23. Fauseweh, B., Pasini, S. & Uhrig, G. Frequency-modulated pulses for quantum bits coupled to time-dependent baths. Phys. Rev. A 85, 022310 (2012).

    Article  ADS  Google Scholar 

  24. Ticozzi, F., Nishio, K. & Altafini, C. Stabilization of stochastic quantum dynamics via open and closed loop control. IEEE Trans. Auto. Control 58, 74–85 (2013).

    Article  MathSciNet  Google Scholar 

  25. Beauchamp, K. G. Walsh Functions and their Applications (Academic, 1975).

    MATH  Google Scholar 

  26. Hayes, D., Khodjasteh, K., Viola, L. & Biercuk, M. J. Reducing sequencing complexity in dynamical quantum error suppression by Walsh modulation. Phys. Rev. A 84, 062323 (2011).

    Article  ADS  Google Scholar 

  27. Owrutsky, P. & Khaneja, N. Control of inhomogeneous ensembles on the Bloch sphere. Phys. Rev. A 86, 022315 (2012).

    Article  ADS  Google Scholar 

  28. Jones, N. C., Ladd, T. D. & Fong, B. H. Dynamical decoupling of a qubit with always-on control fields. New J. Phys. 14, 093045 (2012).

    Article  Google Scholar 

  29. Barthel, C., Medford, J., Marcus, C. M., Hanson, M. P. & Gossard, A. C. Interlaced dynamical decoupling and coherent operation of a singlet–triplet qubit. Phys. Rev. Lett. 105, 266808 (2010).

    Article  ADS  Google Scholar 

  30. Liu, G-Q., Po, H. C., Du, J., Liu, R. B. & Pan, X. Y. Noise-resilient quantum evolution steered by dynamical decoupling. Nature Commun. 4, 2254 (2013).

    Article  ADS  Google Scholar 

  31. Souza, A. M., Álvarez, G. A. & Suter, D. Experimental protection of quantum gates against decoherence and control errors. Phys. Rev. A 86, 050301 (2012).

    Article  ADS  Google Scholar 

  32. van der Sar, T. et al. Decoherence-protected quantum gates for a hybrid solid-state spin register. Nature 484, 82–86 (2012).

    Article  ADS  Google Scholar 

  33. Su, Z-K. & Jiang, S-J. Filter-design perspective applied to dynamical decoupling of a multi-qubit system. J. Phys. B 45, 025502 (2012).

    Article  ADS  Google Scholar 

  34. Silva, G. P. & Viola, L. A general transfer-function approach to noise filtering in open-loop quantum control. Preprint at http://arXiv.org/abs/1408.3836 (2014).

  35. Green, T. J. & Biercuk, M. J. Phase-modulated decoupling and error suppression in qubit-oscillator systems. Preprint at http://arXiv.org/abs/1408.2749 (2014).

Download references

Acknowledgements

We thank P. Fisk, M. Lawn, M. Wouters and B. Warrington for technical assistance and K. Brown, J. T. Merrill and L. Viola for useful discussions. This work partially supported by the US Army Research Office under Contract Number W911NF-11-1-0068, the Australian Research Council Centre of Excellence for Engineered Quantum Systems CE110001013, the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), through the Army Research Office, and the Lockheed Martin Corporation. X.Z. acknowledges useful discussions with G. L. Long and support from the National Natural Science Foundation of China (Grants No. 11175094 and No. 91221205) and the National Basic Research Program of China (No. 2011CB9216002).

Author information

Author notes

  1. D. Hayes

    Present address: Present address: Lockheed Martin Corporation, USA.,

  2. A. Soare and H. Ball: These authors contributed equally to this work.

Authors and Affiliations

  1. ARC Centre for Engineered Quantum Systems, School of Physics, The University of Sydney, NSW 2006, Australia

    A. Soare, H. Ball, D. Hayes, J. Sastrawan, M. C. Jarratt, J. J. McLoughlin, T. J. Green & M. J. Biercuk

  2. National Measurement Institute, West Lindfield, NSW 2070, Australia

    A. Soare, H. Ball, D. Hayes, J. Sastrawan, M. C. Jarratt, J. J. McLoughlin, T. J. Green & M. J. Biercuk

  3. State Key Laboratory of Low-dimensional Quantum Physics and Department of Physics, Tsinghua University, Beijing 100084, China

    X. Zhen

Authors
  1. A. Soare
    View author publications

    Search author on:PubMed Google Scholar

  2. H. Ball
    View author publications

    Search author on:PubMed Google Scholar

  3. D. Hayes
    View author publications

    Search author on:PubMed Google Scholar

  4. J. Sastrawan
    View author publications

    Search author on:PubMed Google Scholar

  5. M. C. Jarratt
    View author publications

    Search author on:PubMed Google Scholar

  6. J. J. McLoughlin
    View author publications

    Search author on:PubMed Google Scholar

  7. X. Zhen
    View author publications

    Search author on:PubMed Google Scholar

  8. T. J. Green
    View author publications

    Search author on:PubMed Google Scholar

  9. M. J. Biercuk
    View author publications

    Search author on:PubMed Google Scholar

Contributions

A.S., H.B., D.H. and M.J.B. conceived and performed the experiments, built experimental apparatus, contributed to data analysis and wrote the manuscript. T.J.G. conceived the relevant theoretical constructs. J.S., M.C.J. and X.Z. assisted with development of the experimental system and data collection. J.J.M. assisted with data collection.

Corresponding author

Correspondence to M. J. Biercuk.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 1985 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Soare, A., Ball, H., Hayes, D. et al. Experimental noise filtering by quantum control. Nature Phys 10, 825–829 (2014). https://doi.org/10.1038/nphys3115

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys3115

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing