Abstract
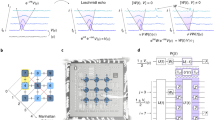
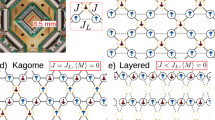
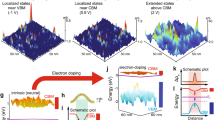
Long-range correlations in two-dimensional (2D) systems are significantly altered by disorder potentials. Theory has predicted the existence of disorder-induced phenomena, such as Anderson localization1 or the emergence of a Bose glass2. More recently, it has been shown that when disorder breaks 2D continuous symmetry, long-range correlations can be enhanced3. Experimentally, developments in quantum gases have allowed the observation of the effects of competition between interaction and disorder4,5. However, experiments exploring the effect of symmetry-breaking disorder are lacking. Here, we create a 2D vortex lattice at 0.1 K in a superconducting thin film with a well-defined 1D thickness modulation—the symmetry-breaking disorder—and track the field-induced modification using scanning tunnelling microscopy. We find that the 1D modulation becomes incommensurate with the vortex lattice and drives an order–disorder transition, behaving as a scale-invariant disorder potential. We show that the transition occurs in two steps and is mediated by the proliferation of topological defects. The resulting critical exponents determining the loss of positional and orientational order are far above theoretical expectations for scale-invariant disorder6,7,8 and follow instead the critical behaviour describing dislocation unbinding melting9,10. Our data show that randomness disorders a 2D crystal, with enhanced long-range correlations due to the presence of a 1D modulation.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Anderson, P. W. Absence of diffusion in certain random lattices. Phys. Rev. 109, 1492–1505 (1958).
Fisher, M., Weichman, P., Grinstein, G. & Fisher, D. Boson localization and the superfluid–insulator transition. Phys. Rev. B 40, 546–570 (1989).
Wehr, J., Niederberger, A., Sanchez-Palencia, L. & Lewenstein, M. Disorder versus the Mermin–Wagner–Hohenberg effect: From classical spin systems to ultracold atomic gases. Phys. Rev. B 74, 224448 (2006).
Billy, J. et al. Direct observation of Anderson localization of matter waves in a controlled disorder. Nature 453, 891–894 (2008).
Sanchez-Palencia, L. & Lewenstein, M. Disordered quantum gases under control. Nature Phys. 6, 87–95 (2010).
Nattermann, T., Scheidl, S., Korshunov, S. & Li, M. Absence of reentrance in the two-dimensional XY-model with random phase shift. J. Phys. 5, 565–572 (1995).
Cha, M-C. & Fertig, H. A. Disorder-induced phase transition in two-dimensional crystals. Phys. Rev. Lett. 74, 4867–4870 (1995).
Nelson, D. R. & Halperin, B. I. Dislocation-mediated melting in two dimensions. Phys. Rev. B 19, 2457–2484 (1979).
Berezinskii, V. Destruction of long-range order in one-dimensional and two-dimensional systems possessing a continuous symmetry group. II. Quantum Systems. Sov. Phys. JETP 34, 610–616 (1972).
Kosterlitz, J. M. & Thouless, D. J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 6, 1181–1203 (1973).
Carpentier, D. & Doussal, P. L. Melting of two-dimensional solids on disordered substrates. Phys. Rev. Lett. 81, 1881–1884 (1998).
Nattermann, T. Scaling approach to pinning: Charge density waves and giant flux creep in superconductors. Phys. Rev. Lett. 64, 2454–2457 (1990).
Minnhagen, P. The two-dimensional Coulomb gas, vortex unbinding, and superfluid-superconducting films. Rev. Mod. Phys. 59, 1001–1066 (1987).
Mermin, N. D. Crystalline order in two dimensions. Phys. Rev. 176, 250–254 (1968).
Hohenberg, P. Existence of long-range order in one and two dimensions. Phys. Rev. 158, 383–366 (1967).
Halperin, B. I. & Nelson, D. R. Theory of two-dimensional melting. Phys. Rev. Lett. 41, 121–124 (1978).
Young, A. P. Melting and the vector Coulomb gas in two dimensions. Phys. Rev. B 19, 1855–1866 (1979).
Nelson, D. R. Reentrant melting in solid films with quenched random impurities. Phys. Rev. B 27, 2902–2914 (1983).
LeDoussal, P. & Giamarchi, T. Dislocation and Bragg glasses in two dimensions. Physica C C331, 233–240 (2000).
Guillamon, I. et al. Direct observation of stress accumulation and relaxation in small bundles of superconducting vortices in tungsten thin films. Phys. Rev. Lett. 106, 077001 (2011).
Korshunov, S. & Nattermann, T. Phase diagram of a Josephson junction array with positional disorder. Physica B 222, 280–286 (1996).
SadrLahijany, M., Ray, P. & Stanley, H. Dispersity-driven melting transition in two-dimensional solids. Phys. Rev. Lett. 79, 3206–3209 (1997).
Abanin, D., Lee, P. & Levitov, L. Randomness-induced XY ordering in a graphene quantum Hall ferromagnet. Phys. Rev. Lett. 98, 156801 (2007).
Niederberger, A. et al. Disorder-induced order in two-component Bose–Einstein condensates. Phys. Rev. Lett. 100, 030403 (2008).
Radzihovsky, L., Frey, E. & Nelson, D. Novel phases and reentrant melting of two-dimensional colloidal crystals. Phys. Rev. E 63, 031503 (2001).
Martinoli, P. Static and dynamic interaction of superconducting vortices with a periodic pinning potential. Phys. Rev. B 17, 1175–1194 (1978).
Giamarchi, T. & LeDoussal, P. Elastic theory of flux lattices in the presence of weak disorder. Phys. Rev. B 52, 1242–1270 (1995).
Zahn, K., Lenke, R. & Maret, G. Two-stage melting of paramagnetic colloidal crystals in two dimensions. Phys. Rev. Lett. 82, 2721–2724 (1999).
Carpentier, D. & Doussal, P. L. Topological transitions and freezing in XY models and Coulomb gases with quenched disorder: Renormalization via traveling waves. Nucl. Phys. B 588, 565–629 (2000).
Herrera-Velarde, S. & von Grünberg, H. H. Disorder-induced vs temperature-induced melting of two-dimensional colloidal crystals. Soft Matter 5, 391–399 (2009).
Acknowledgements
This work was supported by the Spanish MINECO (FIS2011-23488, MAT2011-27553-C02, MAT 2012-38318-C03, Consolider Ingenio Molecular Nanoscience CSD2007-00010), the Comunidad de Madrid through program Nanobiomagnet (S2009/MAT-1726) and by the Marie Curie Actions under the project FP7-PEOPLE-2013-CIG-618321 and contract no. FP7-PEOPLE-2010-IEF-273105. We acknowledge the technical support of UAM’s workshop SEGAINVEX.
Author information
Authors and Affiliations
Contributions
I.G. carried out the experiment, analysis and interpretation of data. I.G. wrote the paper together with H.S. and S.V. Samples were made and characterized by R.C. and J.S. J.M.D.T. and M.R.I. supervised the sample design and fabrication. All authors discussed the manuscript text and contributed to it.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 4176 kb)
Supplementary Movie
Supplementary Movie 1 (AVI 3146 kb)
Supplementary Movie
Supplementary Movie 2 (AVI 3346 kb)
Rights and permissions
About this article
Cite this article
Guillamón, I., Córdoba, R., Sesé, J. et al. Enhancement of long-range correlations in a 2D vortex lattice by an incommensurate 1D disorder potential. Nature Phys 10, 851–856 (2014). https://doi.org/10.1038/nphys3132
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/nphys3132
This article is cited by
-
Ordering of room-temperature magnetic skyrmions in a polar van der Waals magnet
Nature Communications (2023)
-
Melting of a skyrmion lattice to a skyrmion liquid via a hexatic phase
Nature Nanotechnology (2020)
-
Jamming, fragility and pinning phenomena in superconducting vortex systems
Scientific Reports (2020)
-
Dynamics of the Berezinskii–Kosterlitz–Thouless transition in a photon fluid
Nature Photonics (2020)
-
Vortices in Bose–Einstein Condensates with Random Depth Optical Lattice
Journal of Low Temperature Physics (2020)