Abstract
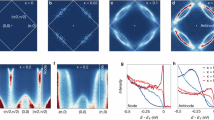
The response of a material to external stimuli depends on its low-energy excitations. In conventional metals, these excitations are electrons on the Fermi surface—a contour in momentum (k) space that encloses all of the occupied states for non-interacting electrons. The pseudogap phase in the copper oxide superconductors, however, is a most unusual state of matter1. It is metallic, but part of its Fermi surface is ‘gapped out’ (refs 2, 3); low-energy electronic excitations occupy disconnected segments known as Fermi arcs4. Two main interpretations of its origin have been proposed: either the pseudogap is a precursor to superconductivity5, or it arises from another order competing with superconductivity6. Using angle-resolved photoemission spectroscopy, we show that the anisotropy of the pseudogap in k-space and the resulting arcs depend only on the ratio T/T*(x), where T*(x) is the temperature below which the pseudogap first develops at a given hole doping x. The arcs collapse linearly with T/T*(x) and extrapolate to zero extent as T→0. This suggests that the T=0 pseudogap state is a nodal liquid—a strange metallic state whose gapless excitations exist only at points in k-space, just as in a d-wave superconducting state.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Timusk, T. & Statt, B. The pseudogap in high-temperature superconductors: An experimental survey. Rep. Prog. Phys. 62, 61–122 (1999).
Ding, H. et al. Spectroscopic evidence for a pseudogap in the normal state of underdoped high-Tc superconductors. Nature 382, 51–54 (1996).
Loeser, A. G. et al. Excitation gap in the normal state of underdoped Bi2Sr2CaCu2O8+δ . Science 273, 325–329 (1996).
Norman, M. R. et al. Destruction of the Fermi surface in underdoped high-Tc superconductors. Nature 392, 157–160 (1998).
Randeria, M. in Proc. Int. School of Physics ‘Enrico Fermi’ on Conventional and High Temperature Superconductors (eds Iadonisi, G., Schrieffer, J. R. & Chiafalo, M. L.) 53–75 (IOS Press, Amsterdam, 1998).
Norman, M. R., Pines, D. & Kallin, C. The pseudogap: friend or foe of high Tc? Adv. Phys. 54, 715–733 (2005).
Norman, M. R., Randeria, M., Ding, H. & Campuzano, J. C. Phenomenology of the low-energy spectral function in high-Tc superconductors. Phys. Rev. B 57, R11093–R11096 (1998).
Ozyuzer, L. et al. Probing the phase diagram of Bi2Sr2CaCu2O8+δ with tunneling spectroscopy. IEEE Trans. Appl. Supercond. 13, 893–896 (2003).
Norman, M. R., Randeria, M., Ding, H. & Campuzano, J. C. Phenomenological models for the gap anisotropy of Bi2Sr2CaCu2O8 as measured by angle-resolved photoemission spectroscopy. Phys. Rev. B 52, 615–622 (1995).
Campuzano, J. C. et al. Electronic spectra and their relation to the (π,π) collective mode in high-Tc superconductors. Phys. Rev. Lett. 83, 3709–3712 (1999).
Nakano, T. et al. Magnetic properties and electronic conduction of superconducting La2−xSrxCuO4 . Phys. Rev. B 49, 16000–16008 (1994).
Wuyts, B. et al. Resistivity and Hall effect of metallic oxygen-deficient YBa2Cu3Ox films in the normal state. Phys. Rev. B 53, 9418–9432 (1996).
Konstantinovic, Z., Li, Z. Z. & Raffy, H. Normal state transport properties of single and double layered Bi2Sr2Can−1CunOy thin films and the pseudogap effect. Physica C 341–348, 859–862 (2000).
Balents, L., Fisher, M. P. A. & Nayak, C. Nodal liquid theory of the pseudo-gap phase of high-Tc superconductors. Int. J. Mod. Phys. B 12, 1033–1068 (1998).
Sutherland, M. et al. Delocalized fermions in underdoped cuprate superconductors. Phys. Rev. Lett. 94, 147004 (2005).
Shen, K. M. et al. Nodal quasiparticles and antinodal charge ordering in Ca2−xNaxCuO2Cl2 . Science 307, 901–904 (2005).
Ding, H. et al. Electronic excitations in Bi2Sr2CaCu2O8+δ: Fermi surface, dispersion, and absence of bilayer splitting. Phys. Rev. Lett. 76, 1533–1536 (1996).
Norman, M. R., Eschrig, M., Kaminski, A. & Campuzano, J. C. Momentum distribution curves in the superconducting state. Phys. Rev. B 64, 184508 (2001).
Kaminski, A. et al. Identifying the background signal in angle-resolved photoemission spectra of high-temperature cuprate superconductors. Phys. Rev. B 69, 212509 (2004).
Acknowledgements
This work was supported by NSF DMR-0305253, the US DOE, Office of Science, under Contract Nos W-31-109-ENG-38 (ANL) and W-7405-Eng-82 (Ames), and the MEXT of Japan. The Synchrotron Radiation Center is supported by NSF DMR-0084402.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
About this article
Cite this article
Kanigel, A., Norman, M., Randeria, M. et al. Evolution of the pseudogap from Fermi arcs to the nodal liquid. Nature Phys 2, 447–451 (2006). https://doi.org/10.1038/nphys334
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/nphys334
This article is cited by
-
Unveiling phase diagram of the lightly doped high-Tc cuprate superconductors with disorder removed
Nature Communications (2023)
-
Monte Carlo study of the pseudogap and superconductivity emerging from quantum magnetic fluctuations
Nature Communications (2022)
-
Explaining the pseudogap through damping and antidamping on the Fermi surface by imaginary spin scattering
Communications Physics (2022)
-
Fermion dynamical symmetry and strongly-correlated electrons: A comprehensive model of high-temperature superconductivity
Frontiers of Physics (2020)
-
Evolution of Pairing Orders between Pseudogap and Superconducting Phases of Cuprate Superconductors
Scientific Reports (2019)