Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Cover times of random searches

Nature Physics volume 11, pages 844–847 (2015)Cite this article

Subjects

Abstract

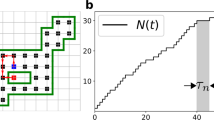
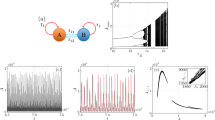
How long must one undertake a random search to visit all sites of a given domain? This time, known as the cover time1, is a key observable to quantify the efficiency of exhaustive searches, which require a complete exploration of an area and not only the discovery of a single target. Examples range from immune-system cells chasing pathogens2 to animals harvesting resources3,4, from robotic exploration for cleaning or demining to the task of improving search algorithms5. Despite its broad relevance, the cover time has remained elusive and so far explicit results have been scarce and mostly limited to regular random walks6,7,8,9. Here we determine the full distribution of the cover time for a broad range of random search processes, including Lévy strategies10,11,12,13,14, intermittent strategies4,15,16, persistent random walks17 and random walks on complex networks18, and reveal its universal features. We show that for all these examples the mean cover time can be minimized, and that the corresponding optimal strategies also minimize the mean search time for a single target, unambiguously pointing towards their robustness.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: How long does it take to exhaustively explore a given domain? This quantity defines the cover time of the domain.
Figure 2: Universal distribution of the full cover time (M = N) for non-compact search processes.
Figure 3: Universal distribution of cover time type observables for non-compact search processes.
Figure 4: The mean full cover time and the mean search time for a single target can be minimized by the same optimal strategy.

Similar content being viewed by others

References

  1. Aldous, D. On the time taken by random walks on finite groups to visit every state. Z. für Wahrscheinlichkeitstheor. Verwandte Geb. 62, 361–374 (1983).

    Article  MathSciNet  Google Scholar 

  2. Heuzé, M. L. et al. Migration of dendritic cells: Physical principles, molecular mechanisms, and functional implications. Immunol. Rev. 256, 240–254 (2013).

    Article  Google Scholar 

  3. Viswanathan, G. M., Raposo, E. P. & da Luz, M. G. E. Lévy flights and superdiffusion in the context of biological encounters and random searches. Phys. Life Rev. 5, 133–150 (2008).

    Article  ADS  Google Scholar 

  4. Bénichou, O., Loverdo, C., Moreau, M. & Voituriez, R. Intermittent search strategies. Rev. Mod. Phys. 83, 81–129 (2011).

    Article  ADS  Google Scholar 

  5. Vergassola, M., Villermaux, E. & Shraiman, B. I. Infotaxis as a strategy for searching without gradients. Nature 445, 406–409 (2007).

    Article  ADS  Google Scholar 

  6. Brummelhuis, M. J. A. M. & Hilhorst, H. J. Covering of a finite lattice by a random walk. Physica A 176, 387–408 (1991).

    Article  ADS  MathSciNet  Google Scholar 

  7. Dembo, A., Peres, Y., Rosen, J. & Zeitouni, O. Cover times for Brownian motion and random walks in two dimensions. Ann. Math. 160, 433–464 (2004).

    Article  MathSciNet  Google Scholar 

  8. Ding, J. On cover times for 2D lattices. Electron. J. Probab. 17, 45 (2012).

    Article  MathSciNet  Google Scholar 

  9. Belius, D. Gumbel fluctuations for cover times in the discrete torus. Probab. Theory Relat. Fields 157, 635–689 (2013).

    Article  MathSciNet  Google Scholar 

  10. Shlesinger, M. F. & Klafter, J. in Lévy Walks vs Lévy Flights (eds Stanley, H. E. & Ostrowski, N.) 279–283 (Springer, 1986).

    Google Scholar 

  11. Viswanathan, G. M. et al. Levy flight search patterns of wandering albatrosses. Nature 381, 413–415 (1996).

    Article  ADS  Google Scholar 

  12. Viswanathan, G. M. et al. Optimizing the success of random searches. Nature 401, 911–914 (1999).

    Article  ADS  Google Scholar 

  13. Metzler, R. & Klafter, J. The random walk’s guide to anomalous diffusion: A fractionnal dynamics approach. Phys. Rep. 339, 1–77 (2000).

    Article  ADS  Google Scholar 

  14. Lomholt, M. A., Tal, K., Metzler, R. & Joseph, K. Lévy strategies in intermittent search processes are advantageous. Proc. Natl Acad. Sci. USA 105, 11055–11059 (2008).

    Article  ADS  Google Scholar 

  15. Benichou, O., Coppey, M., Moreau, M., Suet, P.-H. & Voituriez, R. Optimal search strategies for hidden targets. Phys. Rev. Lett. 94, 198101 (2005).

    Article  ADS  Google Scholar 

  16. Oshanin, G., Wio, H. S., Lindenberg, K. & Burlatsky, S. F. Intermittent random walks for an optimal search strategy: One-dimensional case. J. Phys.: Condens. Matter 19, 065142 (2007).

    ADS  Google Scholar 

  17. Tejedor, V., Voituriez, R. & Bénichou, O. Optimizing persistent random searches. Phys. Rev. Lett. 108, 088103 (2012).

    Article  ADS  Google Scholar 

  18. Condamin, S., Benichou, O., Tejedor, V., Voituriez, R. & Klafter, J. First-passage times in complex scale-invariant media. Nature 450, 77–80 (2007).

    Article  ADS  Google Scholar 

  19. Redner, S. A Guide to First-Passage Processes (Cambridge Univ. Press, 2001).

    Book  Google Scholar 

  20. Bénichou, O., Chevalier, C., Klafter, J., Meyer, B. & Voituriez, R. Geometry-controlled kinetics. Nature Chem. 2, 472–477 (2010).

    Article  ADS  Google Scholar 

  21. Bénichou, O. & Voituriez, R. From first-passage times of random walks in confinement to geometry-controlled kinetics. Phys. Rep. 539, 225–284 (2014).

    Article  ADS  MathSciNet  Google Scholar 

  22. Bray, A. J., Majumdar, S. N. & Schehr, G. Persistence and first-passage properties in nonequilibrium systems. Adv. Phys. 62, 225–361 (2013).

    Article  ADS  Google Scholar 

  23. Aldous, D. An introduction to covering problems for random walks on graphs. J. Theor. Probab. 2, 87–89 (1989).

    Article  MathSciNet  Google Scholar 

  24. Weiss, G. & Shlesinger, M. On the expected number of distinct points in a subset visited by ann-step random walk. J. Stat. Phys. 27, 355–363 (1982).

    Article  ADS  Google Scholar 

  25. Burov, S. & Barkai, E. Weak subordination breaking for the quenched trap model. Phys. Rev. E 86, 041137 (2012).

    Article  ADS  Google Scholar 

  26. Yokoi, C. S. O., Hernández-Machado, A. & Ramírez-Piscina, L. Some exact results for the lattice covering time problem. Phys. Lett. A 145, 82–86 (1990).

    Article  ADS  MathSciNet  Google Scholar 

  27. Nemirovsky, A. M., Mártin, H. O. & Coutinho-Filho, M. D. Universality in the lattice-covering time problem. Phys. Rev. A 41, 761–767 (1990).

    Article  ADS  Google Scholar 

  28. Hughes, B. Random Walks and Random Environments (Oxford Univ. Press, 1995).

    MATH  Google Scholar 

  29. Meyer, B., Chevalier, C., Voituriez, R. & Bénichou, O. Universality classes of first-passage-time distribution in confined media. Phys. Rev. E 83, 051116 (2011).

    Article  ADS  Google Scholar 

  30. Bénichou, O., Chevalier, C., Meyer, B. & Voituriez, R. Facilitated diffusion of proteins on chromatin. Phys. Rev. Lett. 106, 038102 (2011).

    Article  ADS  Google Scholar 

  31. Albert, R. & Barabasi, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2001).

    Article  ADS  MathSciNet  Google Scholar 

  32. Benichou, O., Moreau, M., Suet, P.-H. & Voituriez, R. Intermittent search process and teleportation. J. Chem. Phys. 126, 234109 (2007).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

O.B. was supported by ERC grant FPTOpt-277998.

Author information

Authors and Affiliations

  1. Laboratoire de Physique Théorique de la Matière Condensée, UMR 7600 CNRS /UPMC, 4 Place Jussieu 75255 Paris Cedex, France,

    Marie Chupeau, Olivier Bénichou & Raphaël Voituriez

  2. Laboratoire Jean Perrin, UMR 8237 CNRS /UPMC, 4 Place Jussieu 75255 Paris Cedex, France,

    Raphaël Voituriez

Authors
  1. Marie Chupeau
    View author publications

    Search author on:PubMed Google Scholar

  2. Olivier Bénichou
    View author publications

    Search author on:PubMed Google Scholar

  3. Raphaël Voituriez
    View author publications

    Search author on:PubMed Google Scholar

Contributions

All authors contributed equally to this work.

Corresponding authors

Correspondence to Olivier Bénichou or Raphaël Voituriez.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 520 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chupeau, M., Bénichou, O. & Voituriez, R. Cover times of random searches. Nature Phys 11, 844–847 (2015). https://doi.org/10.1038/nphys3413

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys3413

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing