Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Synthetic gauge flux and Weyl points in acoustic systems

Nature Physics volume 11, pages 920–924 (2015)Cite this article

Subjects

Abstract

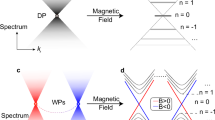
Following the discovery of the quantum Hall effect1,2 and topological insulators3,4, the topological properties of classical waves began to draw attention5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21. Topologically non-trivial bands characterized by non-zero Chern numbers are realized through either the breaking of time-reversal symmetry using an external magnetic field5,6,7,15,16 or dynamic modulation8,17. Owing to the absence of a Faraday-like effect, the breaking of time-reversal symmetry in an acoustic system is commonly realized with moving background fluids20,22, which drastically increases the engineering complexity. Here we show that we can realize effective inversion symmetry breaking and create an effective gauge flux in a reduced two-dimensional system by engineering interlayer couplings, achieving an acoustic analogue of the topological Haldane model2,23. We show that the synthetic gauge flux is closely related to Weyl points24,25,26 in the three-dimensional band structure and the system supports chiral edge states for fixed values of kz.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Interlayer coupling induces different symmetry breakings in two-dimensional systems.
Figure 2: Different interlayer coupling coefficients induce effective breaking of in-plane inversion symmetry.
Figure 3: Chiral interlayer coupling induces a synthetic gauge flux.
Figure 4: Weyl points in the reciprocal space.

Similar content being viewed by others

References

  1. Klitzing, K. v., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).

    Article  ADS  Google Scholar 

  2. Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: Condensed-matter realization of the “Parity Anomaly”. Phys. Rev. Lett. 61, 2015–2018 (1988).

    Article  ADS  MathSciNet  Google Scholar 

  3. Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).

    Article  ADS  Google Scholar 

  4. Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).

    Article  ADS  Google Scholar 

  5. Haldane, F. D. M. & Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 100, 013904 (2008).

    Article  ADS  Google Scholar 

  6. Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).

    Article  ADS  Google Scholar 

  7. Wang, Z., Chong, Y. D., Joannopoulos, J. D. & Soljačić, M. Reflection-free one-way edge modes in a gyromagnetic photonic crystal. Phys. Rev. Lett. 100, 013905 (2008).

    Article  ADS  Google Scholar 

  8. Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).

    Article  ADS  Google Scholar 

  9. Hafezi, M., Demler, E. A., Lukin, M. D. & Taylor, J. M. Robust optical delay lines with topological protection. Nature Phys. 7, 907–912 (2011).

    Article  ADS  Google Scholar 

  10. Hafezi, M., Mittal, S., Fan, J., Migdall, A. & Taylor, J. M. Imaging topological edge states in silicon photonics. Nature Photon. 7, 1001–1005 (2013).

    Article  ADS  Google Scholar 

  11. Khanikaev, A. B. et al. Photonic topological insulators. Nature Mater. 12, 233–239 (2013).

    Article  ADS  Google Scholar 

  12. Chen, W.-J. et al. Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide. Nature Commun. 5, 6782 (2014).

    Google Scholar 

  13. Liang, G. Q. & Chong, Y. D. Optical resonator analog of a two-dimensional topological insulator. Phys. Rev. Lett. 110, 203904 (2013).

    Article  ADS  Google Scholar 

  14. Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological photonics. Nature Photon. 8, 821–829 (2014).

    Article  ADS  Google Scholar 

  15. Skirlo, S. A., Lu, L. & Soljačić, M. Multimode one-way waveguides of large Chern numbers. Phys. Rev. Lett. 113, 113904 (2014).

    Article  ADS  Google Scholar 

  16. He, W.-Y. & Chan, C. T. The emergence of Dirac points in photonic crystals with mirror symmetry. Sci. Rep. 5, 8186 (2015).

    Article  Google Scholar 

  17. Fang, K., Yu, Z. & Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nature Photon. 6, 782–787 (2012).

    Article  ADS  Google Scholar 

  18. Prodan, E. & Prodan, C. Topological phonon modes and their role in dynamic instability of microtubules. Phys. Rev. Lett. 103, 248101 (2009).

    Article  ADS  Google Scholar 

  19. Xiao, M. et al. Geometric phase and band inversion in periodic acoustic systems. Nature Phys. 11, 240–244 (2015).

    Article  ADS  Google Scholar 

  20. Yang, Z. et al. Topological acoustics. Phys. Rev. Lett. 114, 114301 (2015).

    Article  ADS  Google Scholar 

  21. Kane, C. L. & Lubensky, T. C. Topological boundary modes in isostatic lattices. Nature Phys. 10, 39–45 (2014).

    Article  ADS  Google Scholar 

  22. Fleury, R., Sounas, D. L., Sieck, C. F., Haberman, M. R. & Alù, A. Sound isolation and giant linear nonreciprocity in a compact acoustic circulator. Science 343, 516–519 (2014).

    Article  ADS  Google Scholar 

  23. Jotzu, G. et al. Experimental realization of the topological Haldane model with ultracold fermions. Nature 515, 237–240 (2014).

    Article  ADS  Google Scholar 

  24. Lu, L., Fu, L., Joannopoulos, J. D. & Soljačić, M. Weyl points and line nodes in gyroid photonic crystals. Nature Photon. 7, 294–299 (2013).

    Article  ADS  Google Scholar 

  25. Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).

    Article  ADS  Google Scholar 

  26. Fang, Z. et al. The anomalous Hall effect and magnetic monopoles in momentum space. Science 302, 92–95 (2003).

    Article  ADS  Google Scholar 

  27. Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976).

    Article  ADS  Google Scholar 

  28. Burkov, A. A. & Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107, 127205 (2011).

    Article  ADS  Google Scholar 

  29. Yang, K.-Y., Lu, Y.-M. & Ran, Y. Quantum Hall effects in a Weyl semimetal: Possible application in pyrochlore iridates. Phys. Rev. B 84, 075129 (2011).

    Article  ADS  Google Scholar 

  30. Lu, L. et al. Experimental observation of Weyl points. Science 349, 622–624 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  31. Xu, S.-Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).

    Article  ADS  Google Scholar 

  32. Lv, B. Q. et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015).

    Google Scholar 

  33. Nielsen, H. B. & Ninomiya, M. The Adler–Bell–Jackiw anomaly and Weyl fermions in a crystal. Phys. Lett. B 130, 389–396 (1983).

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors would like to thank Z. Q. Zhang and K. T. Law for discussions. This work was supported by the Hong Kong Research Grants Council (grant no. AoE/P-02/12).

Author information

Author notes

  1. Meng Xiao and Wen-Jie Chen: These authors contributed equally to this work.

Authors and Affiliations

  1. Department of Physics and Institute for Advanced Study, Hong Kong University of Science and Technology, Clear Water Bay, Hong Kong, China

    Meng Xiao, Wen-Jie Chen, Wen-Yu He & C. T. Chan

Authors
  1. Meng Xiao
    View author publications

    Search author on:PubMed Google Scholar

  2. Wen-Jie Chen
    View author publications

    Search author on:PubMed Google Scholar

  3. Wen-Yu He
    View author publications

    Search author on:PubMed Google Scholar

  4. C. T. Chan
    View author publications

    Search author on:PubMed Google Scholar

Contributions

C.T.C. initiated the programme. M.X. and W.-J.C. contributed equally to this work. All authors contributed to the analysis and discussion of the results.

Corresponding author

Correspondence to C. T. Chan.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 1756 kb)

Supplementary information

Supplementary information (GIF 1635 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xiao, M., Chen, WJ., He, WY. et al. Synthetic gauge flux and Weyl points in acoustic systems. Nature Phys 11, 920–924 (2015). https://doi.org/10.1038/nphys3458

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys3458

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing