Modulation of mechanical resonance by chemical potential oscillation in graphene

Abstract

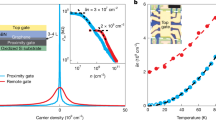
The classical picture of the force on a capacitor assumes a large density of electronic states, such that the electrochemical potential of charges added to the capacitor is given by the external electrostatic potential and the capacitance is determined purely by geometry¹. Here we consider capacitively driven motion of a nano-mechanical resonator with a low density of states, in which these assumptions can break down^2,3,4,5. We find three leading-order corrections to the classical picture: the first of which is a modulation in the static force due to variation in the internal chemical potential; the second and third are changes in the static force and dynamic spring constant due to the rate of change of chemical potential, expressed as the quantum (density of states) capacitance^6,7. As a demonstration, we study capacitively driven graphene mechanical resonators, where the chemical potential is modulated independently of the gate voltage using an applied magnetic field to manipulate the energy of electrons residing in discrete Landau levels^8,9,10. In these devices, we observe large periodic frequency shifts consistent with the three corrections to the classical picture. In devices with extremely low strain and disorder, the first correction term dominates and the resonant frequency closely follows the chemical potential. The theoretical model fits the data with only one adjustable parameter representing disorder-broadening of the Landau levels. The underlying electromechanical coupling mechanism is not limited by the particular choice of material, geometry, or mechanism for variation in the chemical potential, and can thus be extended to other low-dimensional systems.