Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Ferromagnetic and antiferromagnetic order in bacterial vortex lattices

Nature Physics volume 12, pages 341–345 (2016)Cite this article

Subjects

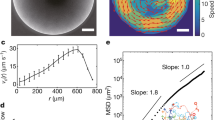
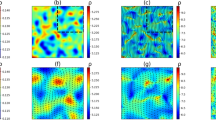
Abstract

Despite their inherently non-equilibrium nature1, living systems can self-organize in highly ordered collective states2,3 that share striking similarities with the thermodynamic equilibrium phases4,5 of conventional condensed-matter and fluid systems. Examples range from the liquid-crystal-like arrangements of bacterial colonies6,7, microbial suspensions8,9 and tissues10 to the coherent macro-scale dynamics in schools of fish11 and flocks of birds12. Yet, the generic mathematical principles that govern the emergence of structure in such artificial13 and biological6,7,8,9,14 systems are elusive. It is not clear when, or even whether, well-established theoretical concepts describing universal thermostatistics of equilibrium systems can capture and classify ordered states of living matter. Here, we connect these two previously disparate regimes: through microfluidic experiments and mathematical modelling, we demonstrate that lattices of hydrodynamically coupled bacterial vortices can spontaneously organize into distinct patterns characterized by ferro- and antiferromagnetic order. The coupling between adjacent vortices can be controlled by tuning the inter-cavity gap widths. The emergence of opposing order regimes is tightly linked to the existence of geometry-induced edge currents15,16, reminiscent of those in quantum systems17,18,19. Our experimental observations can be rationalized in terms of a generic lattice field theory, suggesting that bacterial spin networks belong to the same universality class as a wide range of equilibrium systems.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Edge currents determine antiferromagnetic and ferromagnetic order in a square lattice of bacterial vortices.
Figure 2: Best-fit mean-field LFT model captures the phase transition in the square lattice.
Figure 3: Frustration in triangular lattices determines the preferred order.

Similar content being viewed by others

References

  1. Schrödinger, E. What is Life? (Cambridge Univ. Press, 1944).

    Google Scholar 

  2. Vicsek, T. & Zafeiris, A. Collective motion. Phys. Rep. 517, 71–140 (2012).

    Article  ADS  Google Scholar 

  3. Marchetti, M. C. et al. Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189 (2013).

    Article  ADS  Google Scholar 

  4. Kardar, M. Statistical Physics of Fields (Cambridge Univ. Press, 2007).

    Book  Google Scholar 

  5. Mermin, N. D. The topological theory of defects in ordered media. Rev. Mod. Phys. 51, 591–648 (1979).

    Article  ADS  MathSciNet  Google Scholar 

  6. Ben Jacob, E., Becker, I., Shapira, Y. & Levine, H. Bacterial linguistic communication and social intelligence. Trends Microbiol. 12, 366–372 (2004).

    Article  Google Scholar 

  7. Volfson, D., Cookson, S., Hasty, J. & Tsimring, L. S. Biomechanical ordering of dense cell populations. Proc. Natl Acad. Sci. USA 150, 15346–15351 (2008).

    Article  ADS  Google Scholar 

  8. Riedel, I. H., Kruse, K. & Howard, J. A self-organized vortex array of hydrodynamically entrained sperm cells. Science 309, 300–303 (2005).

    Article  ADS  Google Scholar 

  9. Dunkel, J. et al. Fluid dynamics of bacterial turbulence. Phys. Rev. Lett. 110, 228102 (2013).

    Article  ADS  Google Scholar 

  10. Wu, J., Roman, A.-C., Carvajal-Gonzalez, J. M. & Mlodzik, M. Wg and Wnt4 provide long-range directional input to planar cell polarity orientation in drosophila. Nature Cell Biol. 15, 1045–1055 (2013).

    Article  Google Scholar 

  11. Katz, Y., Ioannou, C. C., Tunstro, K., Huepe, C. & Couzin, I. D. Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl Acad. Sci. USA 108, 18720–18725 (2011).

    Article  ADS  Google Scholar 

  12. Cavagna, A. et al. Scale-free correlations in starling flocks. Proc. Natl Acad. Sci. USA 107, 11865–11870 (2010).

    Article  ADS  Google Scholar 

  13. Sanchez, T., Chen, D. T. N., DeCamp, S. J., Heymann, M. & Dogic, Z. Spontaneous motion in hierarchically assembled active matter. Nature 491, 431–434 (2012).

    Article  ADS  Google Scholar 

  14. Sokolov, A. & Aranson, I. S. Physical properties of collective motion in suspensions of bacteria. Phys. Rev. Lett. 109, 248109 (2012).

    Article  ADS  Google Scholar 

  15. Wioland, H., Woodhouse, F. G., Dunkel, J., Kessler, J. O. & Goldstein, R. E. Confinement stabilizes a bacterial suspension into a spiral vortex. Phys. Rev. Lett. 110, 268102 (2013).

    Article  ADS  Google Scholar 

  16. Lushi, E., Wioland, H. & Goldstein, R. E. Fluid flows created by swimming bacteria drive self-organization in confined suspensions. Proc. Natl Acad. Sci. USA 111, 9733–9738 (2014).

    Article  ADS  Google Scholar 

  17. Büttiker, M. Absence of backscattering in the quantum Hall effect in multiprobe conductors. Phys. Rev. B 38, 9375–9389 (1988).

    Article  ADS  Google Scholar 

  18. Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).

    Article  ADS  Google Scholar 

  19. Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009).

    Article  ADS  Google Scholar 

  20. Wilson, K. G. Confinement of quarks. Phys. Rev. D 10, 2445–2459 (1974).

    Article  ADS  Google Scholar 

  21. Glendenning, N. K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity (Springer, 2000).

    Book  Google Scholar 

  22. Battye, R. A. & Sutcliffe, P. M. Skyrmions with massive pions. Phys. Rev. C 73, 055205 (2006).

    Article  ADS  Google Scholar 

  23. Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nature Nanotech. 8, 899–911 (2013).

    Article  ADS  Google Scholar 

  24. Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005).

    Article  ADS  Google Scholar 

  25. Drut, J. E. & Lähde, T. A. Lattice field theory simulations of graphene. Phys. Rev. B 79, 165425 (2009).

    Article  ADS  Google Scholar 

  26. Fernández, R., Fröhlich, J. & Sokal, A. D. Random Walks, Critical Phenomena, and Triviality in Quantum Field Theory (Springer, 1992).

    Book  Google Scholar 

  27. Woodhouse, F. G. & Goldstein, R. E. Spontaneous circulation of confined active suspensions. Phys. Rev. Lett. 109, 168105 (2012).

    Article  ADS  Google Scholar 

  28. Vaks, V. G., Larkin, A. I. & Ovchinnikov, Y. N. Ising model with interaction between non-nearest neighbors. Sov. Phys. JETP 22, 820–826 (1966).

    ADS  Google Scholar 

  29. Stephenson, J. Ising model with antiferromagnetic next-nearest-neighbor coupling: spin correlations and disorder points. Phys. Rev. B 1, 4405–4409 (1970).

    Article  ADS  Google Scholar 

  30. Abo-Shaeer, J. R., Raman, C., Vogels, J. M. & Ketterle, W. Observation of vortex lattices in Bose–Einstein condensates. Science 292, 476–479 (2001).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank V. Kantsler and E. Lushi for assistance and discussions. This work was supported by European Research Council Advanced Investigator Grant 247333 (H.W. and R.E.G.), EPSRC (H.W. and R.E.G.), an MIT Solomon Buchsbaum Fund Award (J.D.) and an Alfred P. Sloan Research Fellowship (J.D.).

Author information

Author notes

  1. Hugo Wioland & Francis G. Woodhouse

    Present address: Present addresses: Institut Jacques Monod, Centre Nationale pour la Recherche Scientifique (CNRS), UMR 7592, Université Paris Diderot, Sorbonne Paris Cité, F-75205 Paris, France (H.W.); Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WB, UK (F.G.W.).,

Authors and Affiliations

  1. Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WB, UK

    Hugo Wioland, Francis G. Woodhouse & Raymond E. Goldstein

  2. Institut Jacques Monod, Centre Nationale pour la Recherche Scientifique (CNRS), UMR 7592, Université Paris Diderot, Sorbonne Paris Cité, F-75205 Paris, France

    Hugo Wioland

  3. Faculty of Engineering, Computing and Mathematics, The University of Western Australia, 35 Stirling Highway, Crawley, Perth, Western Australia 6009, Australia

    Francis G. Woodhouse

  4. Department of Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139-4307, USA

    Jörn Dunkel

Authors
  1. Hugo Wioland
    View author publications

    Search author on:PubMed Google Scholar

  2. Francis G. Woodhouse
    View author publications

    Search author on:PubMed Google Scholar

  3. Jörn Dunkel
    View author publications

    Search author on:PubMed Google Scholar

  4. Raymond E. Goldstein
    View author publications

    Search author on:PubMed Google Scholar

Contributions

All authors designed the research and collaborated on theory. H.W. performed experiments and PIV analysis. H.W. and F.G.W. analysed PIV data and performed parameter inference. F.G.W. and J.D. wrote simulation code. All authors wrote the paper.

Corresponding author

Correspondence to Raymond E. Goldstein.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information (PDF 1674 kb)

Supplementary Movie 1

Supplementary Movie (MOV 17940 kb)

Supplementary Movie 2

Supplementary Movie (MOV 20802 kb)

Supplementary Movie 3

Supplementary Movie (MOV 5829 kb)

Supplementary Movie 4

Supplementary Movie (MOV 17069 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wioland, H., Woodhouse, F., Dunkel, J. et al. Ferromagnetic and antiferromagnetic order in bacterial vortex lattices. Nature Phys 12, 341–345 (2016). https://doi.org/10.1038/nphys3607

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys3607

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing