Abstract
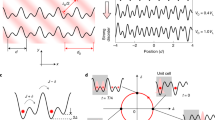
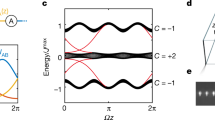
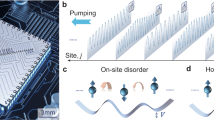
An electron gas in a one-dimensional periodic potential can be transported even in the absence of a voltage bias if the potential is slowly and periodically modulated in time. Remarkably, the transferred charge per cycle is sensitive only to the topology of the path in parameter space. Although this so-called Thouless charge pump was first proposed more than thirty years ago1, it has not yet been realized. Here we report the demonstration of topological Thouless pumping using ultracold fermionic atoms in a dynamically controlled optical superlattice. We observe a shift of the atomic cloud as a result of pumping, and extract the topological invariance of the pumping process from this shift. We demonstrate the topological nature of the Thouless pump by varying the topology of the pumping path and verify that the topological pump indeed works in the quantum regime by varying the speed and temperature.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Thouless, D. J. Quantization of particle transport. Phys. Rev. B 27, 6083–6087 (1983).
Mermin, N. D. The topological theory of defects in ordered media. Rev. Mod. Phys. 51, 591–648 (1979).
Thouless, D. J. Topological Quantum Numbers in Nonrelativistic Physics (World Scientific, 1998).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Klitzing, K. v., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).
Altshuler, B. L. & Glazman, L. I. Pumping electrons. Science 283, 1864–1865 (1999).
Switkes, M., Marcus, C. M., Campman, K. & Gossard, A. C. An adiabatic quantum electron pump. Science 283, 1905–1908 (1999).
Blumenthal, M. D. et al. Gigahertz quantized charge pumping. Nature Phys. 3, 343–347 (2007).
Kaestner, B. et al. Single-parameter nonadiabatic quantized charge pumping. Phys. Rev. B 77, 153301 (2008).
Shilton, J. M. et al. High-frequency single-electron transport in a quasi-one-dimensional GaAs channel induced by surface acoustic waves. J. Phys. Condens. Matter 8, L531–L539 (1996).
Aidelsburger, M. et al. Realization of the Hofstadter Hamiltonian with ultracold atoms in optical lattices. Phys. Rev. Lett. 111, 185301 (2013).
Miyake, H., Siviloglou, G. A., Kennedy, C. J., Burton, W. C. & Ketterle, W. Realizing the Harper Hamiltonian with laser-assisted tunneling in optical lattices. Phys. Rev. Lett. 111, 185302 (2013).
Jotzu, G. et al. Experimental realization of the topological Haldane model with ultracold fermions. Nature 515, 237–240 (2014).
Aidelsburger, M. et al. Measuring the Chern number of Hofstadter bands with ultracold bosonic atoms. Nature Phys. 11, 162–166 (2015).
Mancini, M. et al. Observation of chiral edge states with neutral fermions in synthetic Hall ribbons. Science 349, 1510–1513 (2015).
Stuhl, B. K., Lu, H.-I., Aycock, L. M., Genkina, D. & Spielman, I. B. Visualizing edge states with an atomic Bose gas in the quantum Hall regime. Science 349, 1514–1518 (2015).
Wang, L., Troyer, M. & Dai, X. Topological charge pumping in a one-dimensional optical lattice. Phys. Rev. Lett. 111, 026802 (2013).
Rice, M. J. & Mele, E. J. Elementary excitations of a linearly conjugated diatomic polymer. Phys. Rev. Lett. 49, 1455–1459 (1982).
Atala, M. et al. Direct measurement of the Zak phase in topological Bloch bands. Nature Phys. 9, 795–800 (2013).
Kitagawa, M. et al. Two-color photoassociation spectroscopy of ytterbium atoms and the precise determinations of s-wave scattering lengths. Phys. Rev. A 77, 012719 (2008).
Qian, Y., Gong, M. & Zhang, C. Quantum transport of bosonic cold atoms in double-well optical lattices. Phys. Rev. A 84, 013608 (2011).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Shen, S.-Q. Topological Insulators: Dirac Equation in Condensed Matters (Springer, 2013).
Brouwer, P. W. Scattering approach to parametric pumping. Phys. Rev. B 58, R10135–R10138 (1998).
Mandel, O. et al. Coherent transport of neutral atoms in spin-dependent optical lattice potentials. Phys. Rev. Lett. 91, 010407 (2003).
Fu, L. & Kane, C. L. Time reversal polarization and a Z2 adiabatic spin pump. Phys. Rev. B 74, 195312 (2006).
Aubry, S. & André, G. Analyticity breaking and Anderson localization in incommensurate lattices. Ann. Isr. Phys. Soc. 3, 133–140 (1980).
Marra, P., Citro, R. & Ortix, C. Fractional quantization of the topological charge pumping in a one-dimensional superlattice. Phys. Rev. B 91, 125411 (2015).
Wei, R. & Mueller, E. J. Anomalous charge pumping in a one-dimensional optical superlattice. Phys. Rev. A 92, 013609 (2015).
Lohse, M. et al. A Thouless quantum pump with ultracold bosonic atoms in an optical superlattice. http://dx.doi.org/10.1038/nphys3584 (2015).
Taie, S. et al. Realization of a SU(2) × SU(6) system of fermions in a cold atomic gas. Phys. Rev. Lett. 105, 190401 (2010).
Taie, S. et al. Coherent driving and freezing of bosonic matter wave in an optical Lieb lattice. Sci. Adv. 1, e1500854 (2015).
Acknowledgements
We thank N. Kawakami, S. Fujimoto, J. Ozaki, T. Fukui, I. Maruyama, Y. Hatsugai and S. Nakamura for valuable discussions and A. Sawada for experimental assistance. This work was supported by the Grant-in-Aid for Scientific Research of JSPS (No. 25220711, No. 26247064, No. 24-1698), and the Impulsing Paradigm Change through Disruptive Technologies (ImPACT) Program. L.W. and M.T. were supported by ERC Advanced Grant SIMCOFE and by the Swiss National Science Foundation through the National Center of Competence in Research Quantum Science and Technology QSIT. L.W. and M.T. acknowledge X. Dai for collaborations on the related topic.
Author information
Authors and Affiliations
Contributions
S.N. and T.T. carried out experiments and the data analysis. S.T. conceived the experimental techniques for the superlattice. T.I. and H.O. contributed to building the superlattice set-up. L.W. carried out the theoretical calculations. Y.T. conducted the whole experiment. All the authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 2997 kb)
Rights and permissions
About this article
Cite this article
Nakajima, S., Tomita, T., Taie, S. et al. Topological Thouless pumping of ultracold fermions. Nature Phys 12, 296–300 (2016). https://doi.org/10.1038/nphys3622
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/nphys3622
This article is cited by
-
Giant piezoelectricity driven by Thouless pump in conjugated polymers
npj Computational Materials (2024)
-
Higher-order topological transport protected by boundary Chern number in phononic crystals
Communications Physics (2024)
-
Laughlin charge pumping in a quantum anomalous Hall insulator
Nature Physics (2023)
-
Quantized fractional Thouless pumping of solitons
Nature Physics (2023)
-
Thouless pumping and topology
Nature Reviews Physics (2023)